0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
(1)顺序表
线性表是具有相同特性的数据元素的一个有限序列
元素个数n=表长度;
n=0(空表)
1<i<n时
ai的直接前驱是ai-1,a1无直接前驱
ai的直接后继是ai+1,an无直接后继
优点:
随机访问性强(物理地址相邻)
查找速度快
获取L中第i个元素
if 1≤i≤ListLength(L)
e=L->data[i-1];
缺点:
插入和删除效率低
可能浪费内存
内存空间要求高,必须有足够的连续内存空间。
数组大小固定,不能动态拓展
顺序表结构体定义
typedef struct
{
int data[MaxSize];//存放顺序表元素
int length ;//存放顺序表的长度
} List,*SqList;
SqList L;//定义顺序表结构体变量
L->data[],L->length//引用
顺序表创建
for(i=0;i<length;i++)
{
cin>>L->data[i];
}
顺序表插入(可拓展为顺序建表)
for (i = 0; i < L->length; i++)
{
if (L->data[i] > x)//找到插入位置
{
for (j = L->length; j > i; j--)//后移
{
L->data[j] = L->data[j - 1];
}
break;
}
}
L->data[i] = x;
L->length++;//长度增一
删除区间数据(法一)
j=0
for (i = 0; i < L->length; i++)
{
//一边扫描一边计算在区间内的数据个数
if (L->data[i] >= min && L->data[i] <= max)
{
j++;
}
else
L->data[i-j]=L->data[i];
}
L->length = L->length - j;//数组长度改变
删除区间数据(法二)
j=0
for (i = 0; i < L->length; i++)
{
//不在删除区间内重构数
if (L->data[i] < min || L->data[i] > max)
{
L->data[j] = L->data[i];
j++;
}
}
L->length = j;//数组长度改变
(2)链表
优点:
插入删除速度快
内存利用率高,不会浪费内存
大小没有固定,拓展很灵活。
缺点:
查找效率低
链表结构体定义
typedef struct LNode
{
int data;
struct LNode* next;
}LNode,*LinkList;
头插法(每次插入都在头节点后) 输入输出顺序相反.
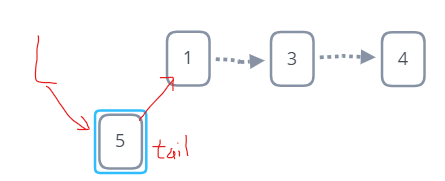
LinkList tail;
L->next = NULL;
for (i = 0; i < n; i++)
{
tail = (LinkList)malloc(sizeof(LNode));
cin >> tail->data;//插入节点
tail->next = L->next;
L->next = tail;
}
尾插法(每次插入都在链尾)
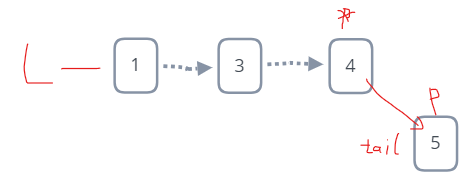
LinkList tail;//插入节点
LinkList p;//最尾部节点
L->next = NULL;
p = L;
for (i = 0; i < n; i++)
{
tail = (LinkList)malloc(sizeof(LNode));
cin >> tail->data;
p->next = tail;
p = tail;
}
p->next=NULL;
尾部加入语句p->next=NULL方便后续链表操作使链表有结尾
数据插入
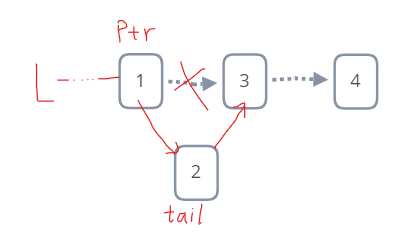
tail=new LNode;
cin>>tail->data;
tail->next=ptr->next;
ptr->next=tail;
删除操作
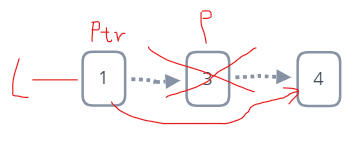
if(p->data=所要删除元素)
ptr->next=p->next;
delete p;
单链表逆置
L = L->next;
ptr = (LinkList)malloc(sizeof(LNode));//新链头节点
ptr->next = NULL;
//头插法将链L中的数据插入链ptr中
while(L!=NULL)
{
pre = (LinkList)malloc(sizeof(LNode));
pre->data = L->data;
pre->next = ptr->next;
ptr->next = pre;
L = L->next;
}
L = ptr;//L指向ptr
(3)有序表(指有一定顺序(递增或递减)排列的线性表)
有序单链表数据插入
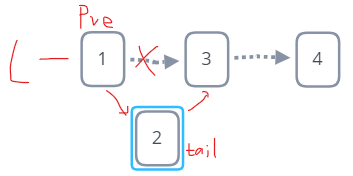
pre=L;
while (pre->next!=NULL && pre->next->data<e)
pre=pre->next; //遍历查找插入位置
tail=new LinkNode;
tail->data=e;//创建存放e的数据结点tail
tail->next=pre->next;//在*pre结点之后插入*p结点
pre->next=tail;
删除
pre=L;
while (pre->next!=NULL && pre->next->data<e)
pre=pre->next; //遍历查找插入位置
if(pre->next->data==e)
tail=new LNode;
tail=pre->next;
pre->next=pre->next->next;//删除节点
delete tail;
有序表合并(顺序表存放)
LC=new SqList; //建立有序顺序表LC
while (i<LA->length && j<LB->length)
{
//分三类将数据存放到LC
if (LA->data[i]<LB->data[j])
else if(LA->data[i]==LB->data[j])
LC->data[k]=LB->data[j];
j++;k++;i++;//相等时两表都要移动
else //LA->data[i]>LB->data[j]
}
while (i<LA->length)//LA尚未扫描完,将其余元素插入LC中
while (j<LB->length)//LB尚未扫描完,将其余元素插入LC中
LC->length=k;//有序表长度改变
(4)循环链表、双链表
双链表
双链表每个节点有2个指针域,一个指向后继节点,一个指向前驱节点
特点:
从任一结点出发可以快速找到其前驱结点和后继结点;
从任一结点出发可以访问其他结点
结构体定义
typedef struct DNode //声明双链表节点类型
{
ElemType data;
struct DNode *prior; //指向前驱节点
struct DNode *next; //指向后继节点
} DLinkList;
插入操作

tail->next = ptr->next
ptr->next->prior = tail
tail->prior = ptr
ptr->next = tail
删除操作

ptr->next->next->prior=ptr;
ptr->next=ptr->next->next;
先改前驱,再改后继
循环链表
循环单链表
从循环链表中的任何一个结点的位置都可以找到其他所有结点,而单链表做不到
循环条件:p!=NULL(单链表)、p!=L (循环单链表) 不带头结点
p->next!=NULL(单链表)、p->next!=L(循环单链表) 带头结点

循环双链表
链表中没有空指针域
p所指结点为尾结点的条件:p->next==L
一步操作即L->prior可以找到尾结点

(5)时间复杂度,空间复杂度
算法的效率主要是看它的时间复杂度和空间复杂度情况
时间复杂度
算法执行语句的次数
选取最高阶的项
条件模糊的一般计算最坏情况
如果算法的执行时间不随着n的增加而增长,时间复杂度是O(1)
空间复杂度
运行过程中临时占用存储空间大小
不随被处理数据量n的大小而改变时,可表示为O(1)
1.2.谈谈你对线性表的认识及学习体会。
线性表:
线性表是n个具有相同特性的数据元素的有限序列;
大部分线性表数据元素之间是一对一的关系,除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的(循环链表也算线性表);
体会:
线性表中涉及数组和链表的问题上学期就已经有了解,数组还好,但是在链表方面对于后继改变和连接的问题还是很糊,经常写着就后继全都改变,非常窒息
做完一个题集并对比之后,我对链表的连接方式和后继关系有更了解一点点
对于链表需要注意的点:
1、链表最尾端最好要加结束标志NULL,在后续对链表的操作会更方便
2、遍历链表过程中务必考虑指针是否为空,条件判断要分清楚,是ptr!=NULL,还是ptr->next!=NULL
3、没用空间要释放,能节省空间也是链表的好处
4、画链表图能更清楚地理解,更容易有思路
对于顺序表需要注意的点:
1、空间要合适不然容易溢出
2、插入,删除操作后,要注意改变顺序表长度
3、注意有些题目结构体定义的是顺序表最后一个数据的位置
2.PTA实验作业
2.1.题目1:7-2 一元多项式的乘法与加法运算
加法:
遍历两链表
若指数相同,则系数相加(若系数相加后等于零舍弃),存入新链中
乘法:(分别相乘后,多次累加)
令LA遍历一次,LB遍历多次
LB与LA的一项相乘遍历一次后形成的新链转入加法运算
多次累加后的成果就为乘法结果
2.1.1
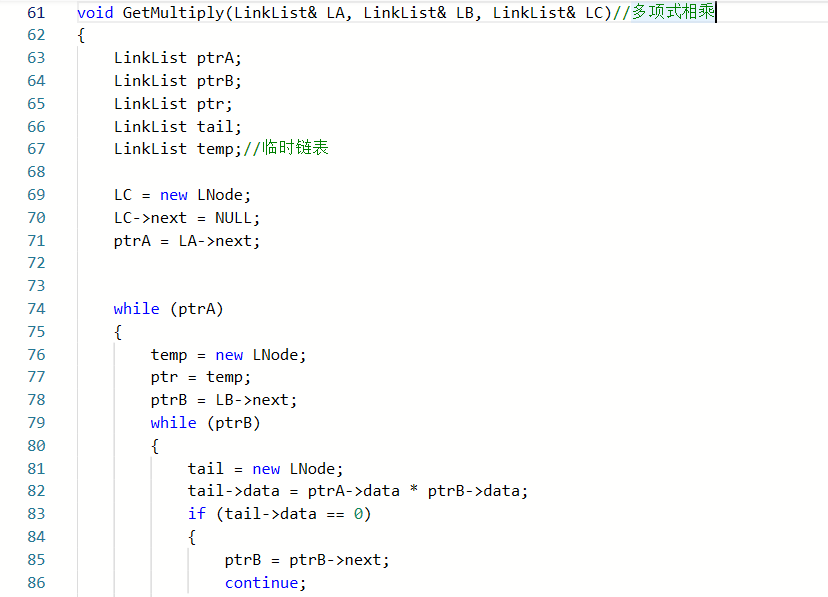
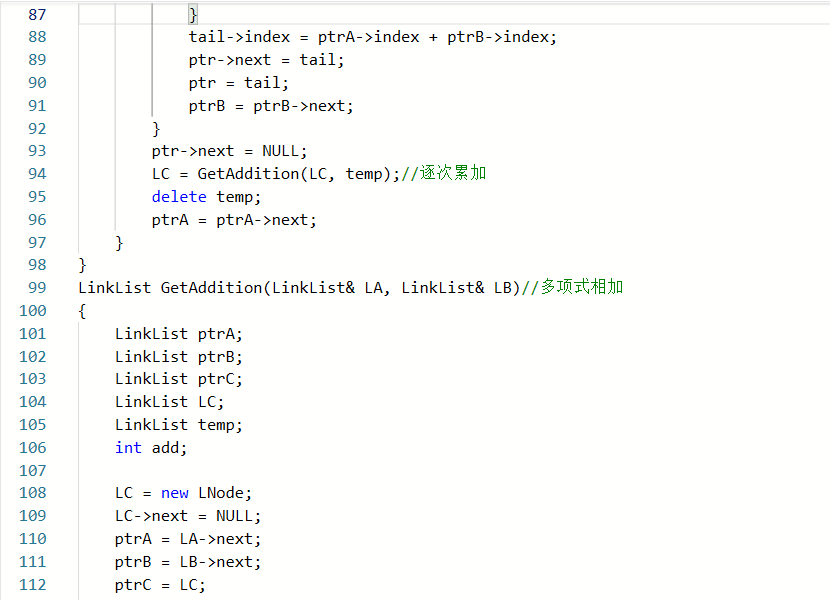
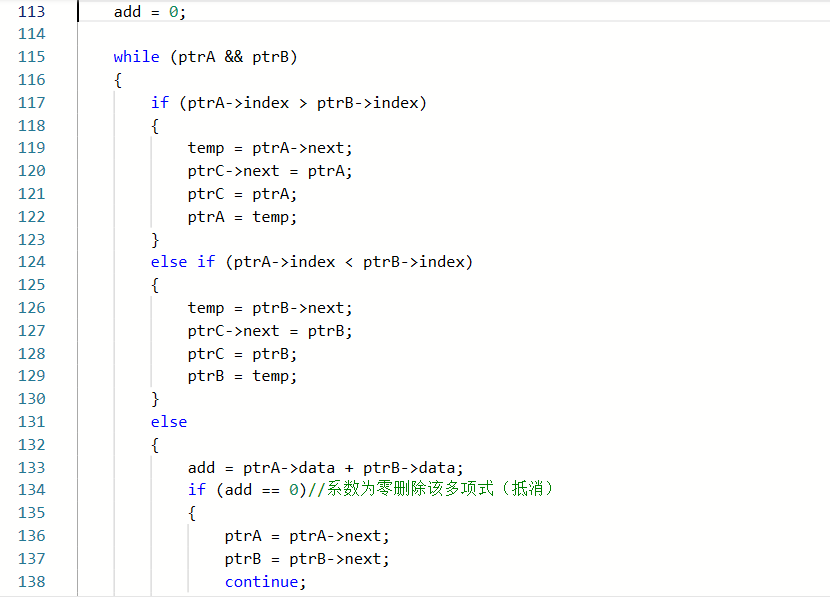

2.1.2本题PTA提交列表说明
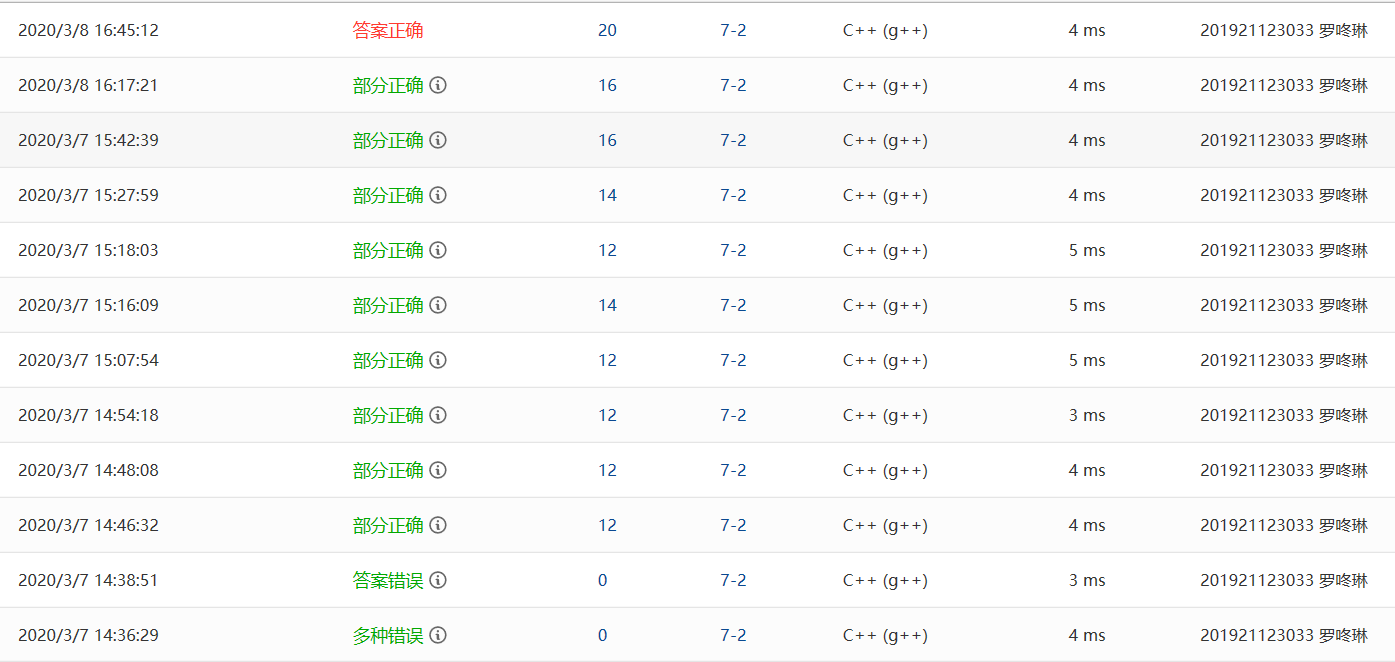
| 错误 | 原因 |
|---|---|
| 多种错误 | LA和LB相乘时,乘完一条链后没有返回链表头部 |
| 答案错误 | 乘法加法输出之间没有换行 |
| 部分正确 | 没考虑到乘法系数为零的情况 |
| 部分正确(输入有零多项式和常数多项式) | 一开始理解为多项式合并后系数为零要输出“0 0”,后来才知道时多项式个数为零 |
部分正确(同类项合并时有抵消)  |
新链LC连接节点后结尾没加NULL若最后一组数据相抵消后LC链尾还是有LA中的数据 |
2.2 6-11 jmu-ds-链表分割

L1正序存放,L2逆序存放(头插法)
L1=L
将所需插入L2数据申请新节点存放后,头插法插入L2链
2.2.1
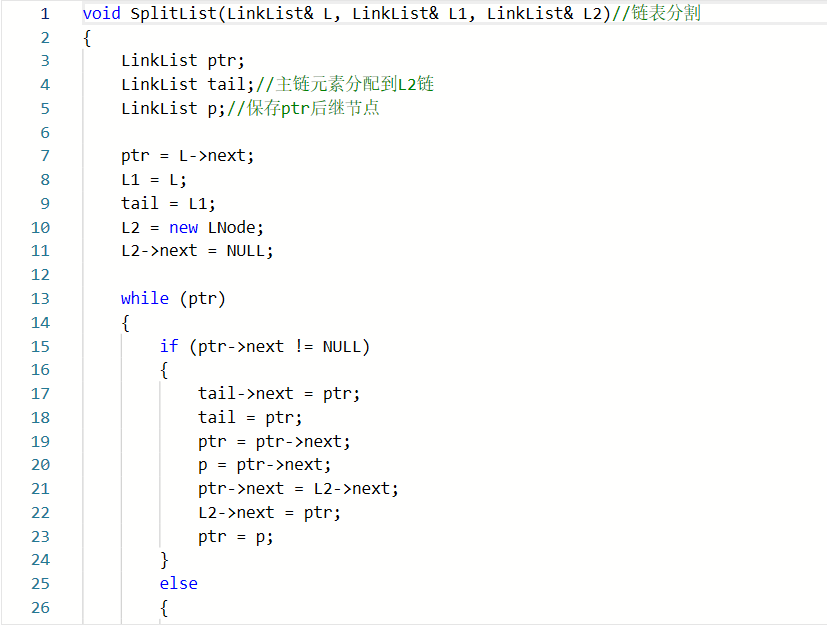
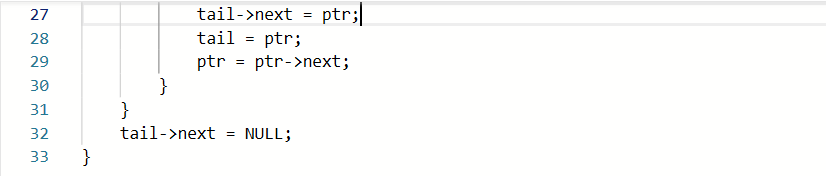
2.2.2本题PTA提交列表说明。

| 错误 | 原因 |
|---|---|
| 段错误 | 在L1,L2申请内存之前将其赋值给其他变量 |
| 运行超时 | ptr遍历指针没向后移动,导致死循环 |
| 多种错误 | 在没有保存后继节点数据的情况下将ptr直接插入另一个链表,导致后继数据节点被修改 |
| 部分正确 | 最尾部没加NULL结束 |
2.3 6-8 jmu-ds-链表倒数第m个数

方法一
遍历链表并将链表逆置,求出节点个数
链表倒数第m个数就是逆置后的链表的第m个数
2.3.1
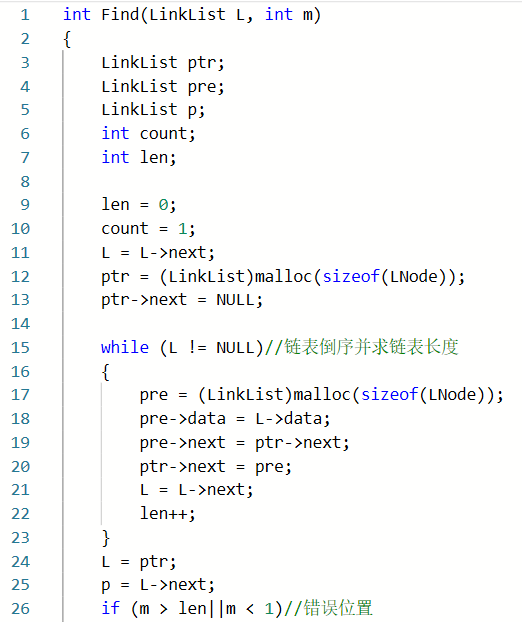
2.3.2本题PTA提交列表说明。

| 错误 | 原因 |
|---|---|
| 部分正确 | 没注意到m > len和m < 1都是错误位置 |
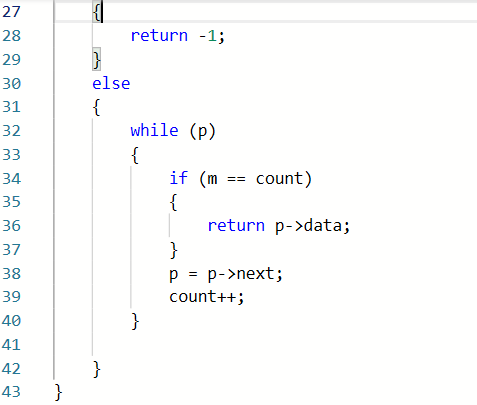
方法二
边移动边找时间复杂度更小,遍历次数更少
//求倒数第k个数
定义count=0记录移动次数
已知带头节点的链L
定义ptr,pre=L
while(ptr)
{
ptr=ptr->next;
count++;
}
ptr向前移动k个节点后pre开始和ptr一起向前移动
pre=pre->next;
当ptr移动到最末尾
while(ptr)
pre所在位置就为倒数第k个数
3.阅读代码
3.1 两两交换链表中的节点
代码:
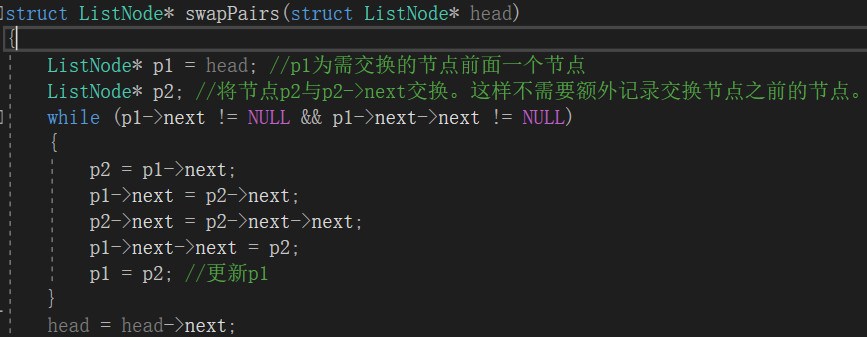
3.1.1 该题的设计思路
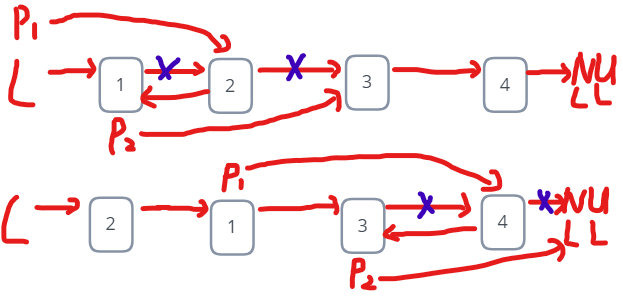
1、p1为需交换的节点前面一个节点
2、将节点p2与p2->next交换,这样就不需要额外记录交换节点之前的节点。
3、更新p1所在位置
3.1.2 该题的伪代码
定义
ListNode* p1=head;
ListNode* p2;
while(p1->next!=NULL&&p1->next->next!=NULL)
{
//将需要交换节点之间next关系逆转
p1移动到需交换的节点前面一个节点
将节点p2与p2->next交换//这样不需要额外记录交换节点之前的节点
p1=p2; //更新p1位置
}
3.1.3 运行结果

3.1.4分析该题目解题优势及难点
优势:
清晰明了,可读性强,
用next关系逆转解决节点交换,在链表上直接实现,不用重新开一条链,节省空间
难点:
用next关系逆转解决节点交换,会使节点后继关系容易混乱,所以移动到的下一个位置的判断和连接关系很重要
更新下一个反转位置时要先储存好后继节点
3.2 K 个一组翻转链表

代码:
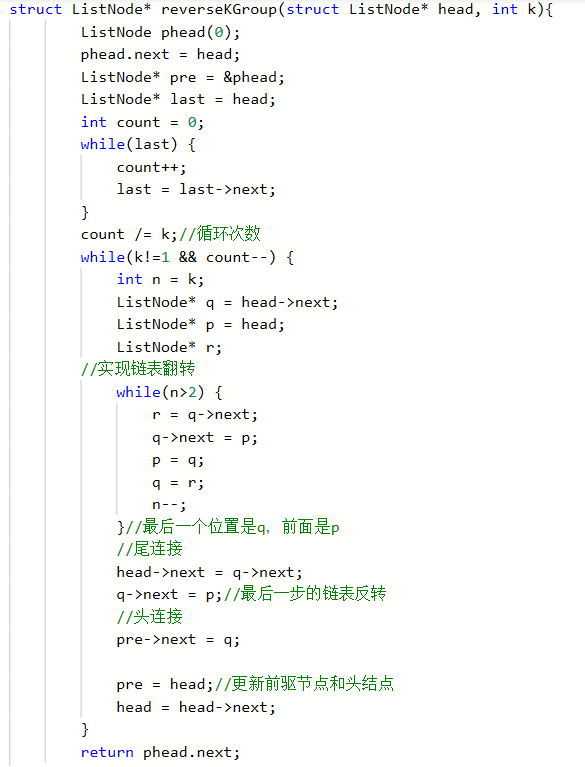
3.2.1 该题的设计思路
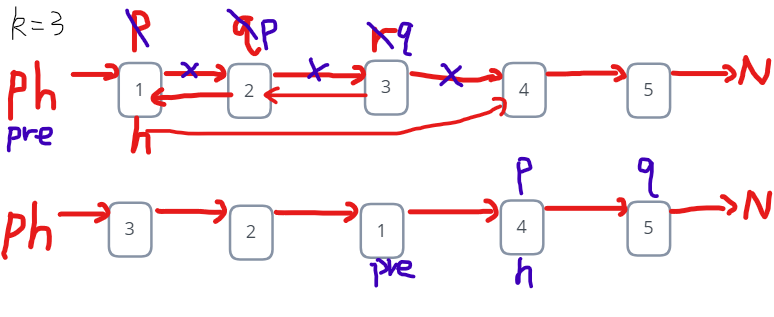
3.2.2 该题的伪代码
while(last)
遍历链表,求链表长度count
求需要循环的次数count /= k;
while(k!=1 && count--)
{
q = head->next;
p = head;
//实现链表翻转
while(n>2)
{
r = q->next;//保留后继节点
改变需要逆转节点之间的next关系
最后使需要逆转的最后一个位置是q,q前面是p
n--;
}
q指向需要反转的最后一个节点,q->next = p实现最后一步的链表反转
的后继节点head->next = q->next;
pre->next = q;
pre = head;更新前驱节点
更新头结点head = head->next;
}
3.2.3 运行结果
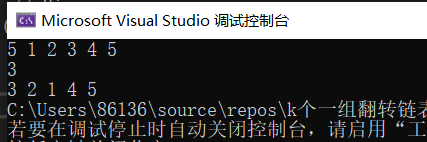
3.2.4分析该题目解题优势及难点
优点:
链表关系运用灵活,可读性强
在链表上直接实现,不用重新开一条链,节省空间
难点:
不带头节点的链表反转时就需要重新申请头节点,反转后头节点也需跟着变动
需要及时更新头节点的位置
最初位置的反转关系不能错乱,更新下一个反转位置时要先储存好后继节点