--------------------siwuxie095
二叉搜索树
这里介绍二叉搜索树(Binary Search Tree)
二叉搜索树,顾名思义,本质上也是一棵二叉树
二叉树在计算机中是一种非常常用的数据结构,选择什么类型的二叉树
很多时候要根据需要解决的问题而定
使用数据结构的核心是要解决问题,而并非是为了使用数据结构而使用
数据结构
使用二叉树并不是因为二叉树很酷,很炫,听起来很专业,而是因为二
叉树能够高效的解决一类问题
二叉搜索树解决的一类问题就是在计算机中非常常见的查找问题
「查找问题是计算机中非常重要的基础问题」
可能很多人会觉得这个问题非常简单,就是在一组数据中找到某
个数据,但是仔细想一想就会发现,查找问题虽然描述出来很简
单,但是它的应用却非常广泛
从去银行办理业务时,银行根据证件号码从系统中调出相应的信
息,到在 Google 中搜索内容时,Google 根据关键字来查找相
关的信息 …
查找问题,是一个听起来非常朴素,实际上却非常困难,被研究
的非常广泛的一类问题
「查找问题,即 Search Problem」
二叉搜索树的优势
事实上,二叉搜索树,通常都用于实现 查找表
有的地方,也称 查找表 为 字典,如下:
key1 | value1 |
key2 | value2 |
key3 | value3 |
key4 | value4 |
key5 | value5 |
即 对于这些数据而言,都是一个一个键值对,即 key-value
对应的数据对,给你一个 key,相应的就有一个 value
这样大量的数据对,集合在一起就形成了一张表,在这张表
中通过键(key)就能直接查到对应的值(value)
最典型的一个应用就是字典。对于一个字典来说,键(key)
就是一个个单词,而值(value)就是单词的释义
这也是查找表有时候也被称为字典这样一种数据结构的原因
如果这些 key 都是整数,而且范围比较小,那么使用数组就可以轻易
地用索引直接来索引到相应的 value
但在实际的业务逻辑中,很多时候不能用整数来表达这样的键(key),
或者是因为这些键(key)相对比较稀疏,使用数组在空间上并不经济,
或者是因为这些键(key)压根就不能用整数来表示
例如:字典的键(key)其实是一个字符串
这种情况下,就需要实现一个查找表,而实现查找表的最基础的一个
方式是实现二叉搜索树
当然,也完全可以用 普通数组 或 顺序数组 来实现这个一个查找表
| 查找元素 | 插入元素 | 删除元素 |
普通数组 | O(n) | O(n) | O(n) |
顺序数组 | O(lgn) | O(n) | O(n) |
二分搜索树 | O(lgn) | O(lgn) | O(lgn) |
可以简单分析一下使用普通数组 或 顺序数组的时间效率:
1)使用普通数组:
查找一个元素,就需要使用 O(n) 的时间从头到尾遍历一遍,看要找的
那个元素在数组的什么位置
插入一个元素,也需要使用 O(n) 的时间从头到尾遍历一遍,因为对于
查找表来说,需要先看一看当前查找表中是否已经含有要插入的元素。
如果没有,再插入;如果有的话,就应该是对 key 相应的 value 进行
一个更新操作
删除一个元素,也需要使用 O(n) 的时间从头到尾遍历一遍,来删除相
应的元素
2)使用顺序数组:
要一直保证这个数组是有序的。这样一来,查找一个元素就可以使用
二分查找法,用 O(lgn) 的时间进行查找,但对于插入一个元素和删除
一个元素来说,依然要使用 O(n) 的时间
相较而言,二叉搜索树就高效很多,它能够保证查找、插入、删除这
三个操作的时间复杂度近乎都是 O(lgn) 级别的
所以,二叉搜索树的优势:
1)高效
不仅可以高效查找数据,还可以高效地插入数据、删除数据 - 动态维护数据
也就是说,如果能一下就把所有的数据拿到手,那可能先对数据进行排序再
使用二分查找法,就足够了
但在很多时候,查找、插入、删除这三个操作,在业务的过程中都是要涉及
的,因此,二叉搜索树提供了一个可以非常高效地动态维护数据的方式
2)可以方便地回答很多数据之间的关系问题,如下:
min、max、floor、ceil、rank、select
可以轻易地找到所有数据中的最小值 min、最大值 max,某个数据的 floor
相应的值、ceil 相应的值,还有给定一个数据,求它的排名 rank,以及找
到所有数据中某排名(如:第 100 名)的数据 select
二叉搜索树的定义
如下图所示,是一棵二叉搜索树:
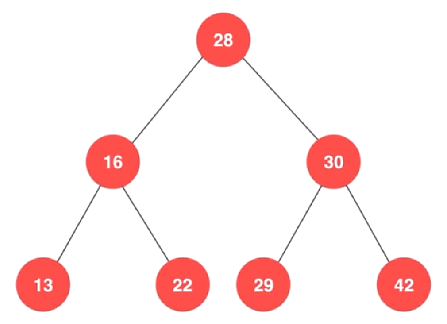
二叉搜索树,是指一棵空树 或者具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值
3)任意节点的左、右子树也分别为二叉搜索树
4)没有键值相等的节点
即
1)每个节点的键值都大于左孩子
2)每个节点的键值都小于右孩子
不难看出,二叉搜索树的定义中天然就包含了递归结构
正因为如此,在对二叉搜索树编程时,很多时候都可以使用递归函数的方式,
方便快速地实现很多功能
注意:对于堆来说,堆的那棵二叉树一定是一棵完全二叉树,但对于二叉搜索
树来说,是没有这个限制的,如下:
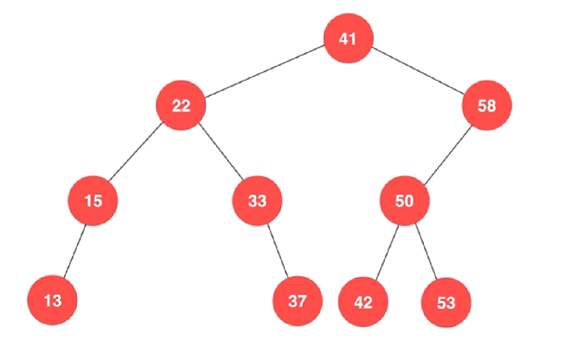
换句话说,上图中的这棵树,也是二叉搜索树,即 二叉搜索树,不一定是
完全二叉树
在实现堆的时候,是利用了堆一定是一棵完全叉树的特点,所以能用数组
来表示堆,但二分搜索树不一定是完全二叉树,所以用数组表示并不方便
因此,通常是设立 Node 节点,来表示 key-value 这样的数据对,而节点
之间的联系,则使用指针的方式来表示
【made by siwuxie095】