匈牙利匹配和最大权值匹配算法

匈牙利匹配和最大权值匹配算法
在使用多目标跟踪算法时，接触到了匈牙利匹配算法，一直没时间好好总结下，现在来填坑。。

1. 基础概念

1.1 二分图

我们之前了解过图(Graph)的概念，图一般可以用G(V, E)来表示，V表示图中的顶点，E表示图中的边。如下面，这个图中有四个顶点，五条边。

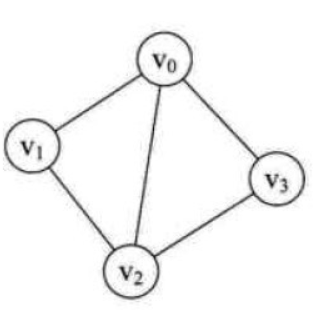
二分图(Bipartite graph)是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连，如下面是一个典型的二分图，图中的点可分为X，Y两部分，X内部的点互补相连，Y内部的点也互不相连。我们也可以发现二分图中一定不存在环。（二分图又称为二部图，偶图）

1.2 二分图匹配

二分图的匹配可以看成是二分图的一个子图，该子图满足以下条件：子图中不存在有任意的两条边依附于同一个顶点

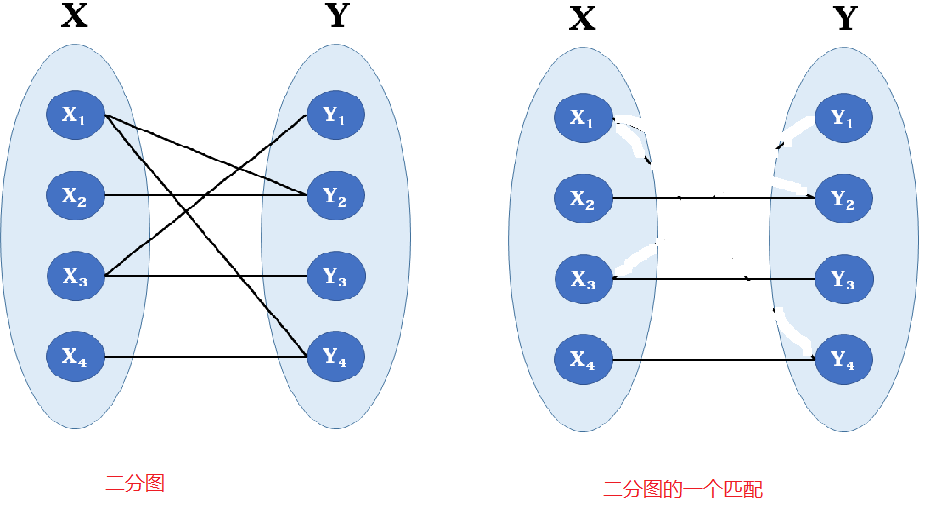
如下面左图是一个二分图，右图就是它的一个匹配，右图中每条边都没有公共端点，可以看出其是二分图的一个子集。概念上有点绕，我们通俗点理解：有一个班级的学生要结成男女两两一组，但每个学生只想自己喜欢的异性结成一组，于是这就会有冲突，而匹配就是要找出这样的男女组成，保证一个男生只和一个女生组合。

二分图的匹配问题在有限资源分配时经常会用到，主要是为了保证某一个资源分且只分到某一个用户的手中

1.3 二分图最大匹配

二分图最大匹配，就是在二分图的所有匹配中，找出边数最大的匹配。还是以上面的情景来理解：有一个班级的学生要结成男女两两一组，但每个学生只想自己喜欢的异性结成一组，匹配是保证一个男生只和一个女生组合，而最大匹配则是尽量保证没有人落单，即二分图最大匹配就是要给出一个最优方案，使得结成的组数最多

匈牙利算法就是寻找二分图最大匹配方案的经典算法

1.4 二分图最大权完美匹配

首先说二分图完美匹配，如果一个二分图的所有点都是匹配点（匹配边中某一条边的端点），则称这个匹配是完美匹配。回到上面的情景，完美匹配就是可以得到一个方案，使得所有男女同学都可以结成两两一组。
- 完美匹配要求二分图两部分的点数相等，因为若X中包括4个点，Y中包含5个点，则Y中必然会有一个点不会被匹配
- 完美匹配一定是最大匹配，最大匹配不一定是完美匹配
二分图最大权完美匹配：假定有一个二分图 G，每条边有一个权值（可为负数），权值和最大的完美匹配是二分图最大权完美匹配。

还有一些概念，二分图最优匹配，二分图最大权值匹配，二分图最小权值匹配(将权值转化为负数，即转为最大权值匹配)，都是指二分图最大权完美匹配。

求解二分图最大权完美匹配一般采用KM(Kuhn-Munkres)匹配算法

2. 匈牙利匹配算法

参考：https://zhuanlan.zhihu.com/p/105212518， https://zhuanlan.zhihu.com/p/104901134?utm_source=wechat_session

2.1 匈牙利算法解析

匈牙利算法(Hungary Algorithm)是由Edmonds在1965年提出的，是求解二分图最大匹配的经典算法，算法的核心就是根据一个初始匹配不停的找增广路，直到没有增广路为止。几个概念如下：
- 交替路：从任意一个未匹配点出发，依次经过未匹配边－匹配边－非匹配边－匹配边－未匹配边……所得到的路径被称为交替路。(即未匹配边和匹配边交替出现)
- 增广路：如果一条交替路的终点是一个未匹配点，那么这条路径是增广路，由于从未匹配点出发，又在未匹配点结束，未匹配边比匹配边多一条。
- 增广路定理：如果可以找到一条增广路，那么将匹配边与未匹配边互换，这个匹配就可以多一条边，否则当前匹配就是最大匹配。即任意一个匹配是最大匹配的充分必要条件是不存在增广路。
增广路互换的实质可以这么考虑，如下图：从未匹配点 A 出发，A 想与 B 匹配，于是通过未匹配边找到 B，然而 B 已经是匹配点，于是只能经过匹配边去问 C 能不能与别人匹配，C 经过未匹配边找到 D，由于 D 是未匹配点，所以 C 成功与 D 匹配。CD 之间的边变为匹配边；BC 之间解除关系，变为未匹配边；AB 之间建立关系，变为匹配边。这便是增广路互换的实质。

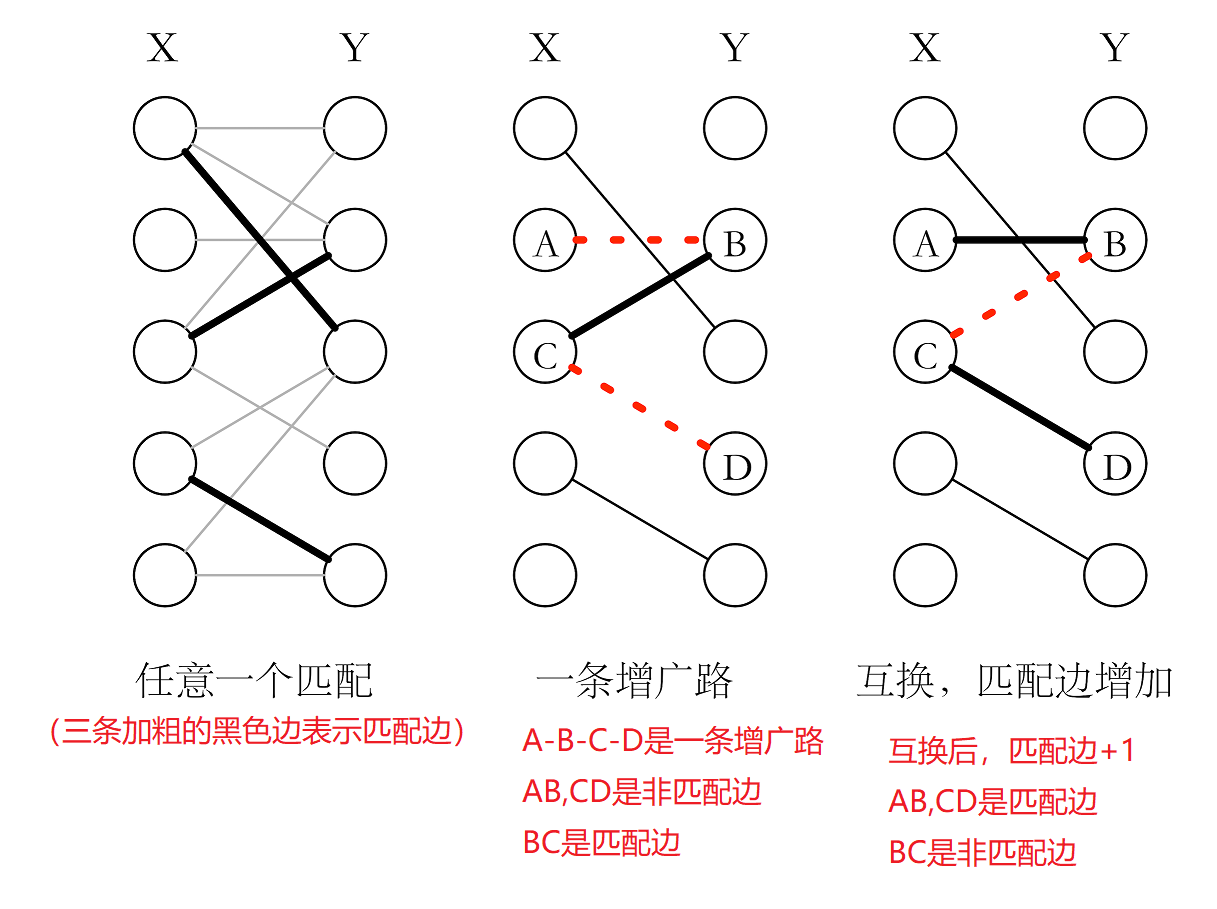
因此，总结下匈牙利算法的思想：就是不断的寻找增广路，如果找到，就互换匹配边和非匹配边，让匹配边增加一条，如果找不到匹配边了，就表示已经是最大匹配了。

2.2 匈牙利算法代码实现

python实现如下：
```
import math
import numpy as np

# 匈牙利匹配算法
class HungaryMatch(object):

    def __init__(self, graph):
        assert isinstance(graph, np.ndarray), print("二分图的必须采用numpy array 格式")
        assert graph.ndim == 2, print("二分图的维度必须为2")
        self.garph = graph
        rows, cols = graph.shape
        self.rows = rows
        self.cols = cols

        # self.vx = np.zeros(cols, dtype=np.int32)   # visit flag, 横向结点的访问标志
        # self.vy = np.zeros(rows, dtype=np.int32)  # visit flag, 竖向结点的访问标志

        self.match_index = np.ones(cols, dtype=np.int32) * -1  # 横向结点匹配的竖向结点的index （默认-1，表示未匹配任何竖向结点）
        self.match_count = 0  # 总共有多少条匹配边

    def match(self):
        for y in range(self.rows):  # 从每一竖向结点开始，寻找增广路
            self.vx = np.zeros(self.cols, dtype=np.int32)  # visit flag, 横向结点的访问标志置0
            self.vy = np.zeros(self.rows, dtype=np.int32)  # visit flag, 竖向结点的访问标志置0
            if self.dfs(y):
                self.match_count += 1  # 采用dfs寻找增广路，如果找到，匹配边加1
        return self.match_index, self.match_count

    def dfs(self, y):  # 递归版深度优先搜索
        self.vy[y] = 1
        for x in range(self.cols):
            if self.vx[x] == 0 and self.garph[y][x] == 1:  # 横向结点x没有访问过，而且竖向结点y和横向结点x有边连接
                self.vx[x] = 1
                # 两种情况：一是结点x没有匹配，那么找到一条增广路；二是X结点已经匹配，采用DFS，沿着X继续往下走，最后若以未匹配点结束，则也是一条增广路
                if self.match_index[x] == -1 or self.dfs(self.match_index[x]):
                    self.match_index[x] = y  # 未匹配边变成匹配边
                    print(y, x, self.match_index)
                    return True
        return False
if __name__ == '__main__':
    graph = np.array([[0, 1, 0, 1], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 1, 0]])
    hungary = HungaryMatch(graph)
    index, count = hungary.match()
    print(index)  # [-1  1  2  0]：三组匹配边(x, y): (1, 1), (2, 2), (3, 0)
    print(count)  # 3：共有三条匹配边        
```
cpp实现如下：

参考：https://zhuanlan.zhihu.com/p/104901134?utm_source=wechat_session
```
bool dfs(int x){
   for(int i=0; i<m; i++){
      if (edge[x][i]==0 || vis[i]) continue;
      vis[i] = true;
      if (y_match[i]==-1 || dfs(y_match[i]))
           return true;
   }
   return false;
}

int cnt = 0;
for (int i=0; i<n; i++){
    memset(vis, false, sizeof(vis));
    if (dfs(i))
         cnt++;
}
```
3. KM算法(Kuhn-Munkres Algorithm)

参考：https://blog.sengxian.com/algorithms/km，https://piggerzzm.github.io/2020/03/28/Kuhn-Munkres/

3.1 可行顶标和相等子图

二分图最优匹配(最大权值匹配)的经典算法是由Kuhn和Munkres独立提出的KM算法，值得一提的是最初的KM算法是在1955年和1957年提出的，因此当时的KM算法是以矩阵为基础的，随着匈牙利算法被Edmonds提出之后，现有的KM算法利用匈牙利树可以得到更漂亮的实现。

KM算法是通过给每个顶点一个标号（叫做顶标，或者节点函数）来把求最大权完美匹配的问题转化为求完美匹配的问题的。可以简单理解为节点函数就是节点的一个值。几个概念如下：
- 顶标(节点函数)：指的是图中的每个顶点，给它赋予一个值(就像边的权重值)，这个值也称为节点函数值。
- 可行顶标：对于所有顶点的函数值(l)，使得对于任意边 (e(x ightarrow y))，都满足 (l_{x} + l_{y} ge W_{e})，（其中，(l_x)为顶点x的顶标，(l_y)为顶点y的顶标，(w_e)为边(e(x ightarrow y))的权值)
- 相等子图：相等子图包含原图中所有的点，但只包含满足 (l_{x} + l_{y} = W_{e})的所有边 (e(x ightarrow y))。根据定义，这些边一定是当前权值最大的边（不等式已经取到等号），那么如果相等子图有完美匹配，那这个完美匹配一定是最大权值完美匹配。因为相等子图的权值和为所有点的顶标之和，而随便一个匹配中的边因为受到 (W_{e} le l_{x} + l_{y})的限制，不可能比所有点的顶标之和大。
3.2 KM算法步骤解析

KM算法的主要目标就在于寻找可行顶标，使得相等子图有完美匹配。可行顶标的修改过程中，每一步都运用了贪心的思想，这样我们的最终结果一定是最优的。下面是算法的叙述：

步骤一：顶标初始化

因为有 (l_{x} + l_{y} = W_{e})恒成立，我们设左侧（Y集）的所有节点顶标为 0，那么所有 X集的点的顶标就必须为从它出发所有的边的权值最大值。

步骤二：寻找完美匹配

寻找当前顶标条件下，采用增广路定理对每个点进行匹配(匈牙利算法)，若最大匹配就是完美匹配，结束算法，否则必须修改顶标，使得有更多的边能够参与进来。

步骤三：修改顶标，加入更多可行顶标及对应边

我们求当前相等子图的完美匹配失败，是因为对于某个未匹配顶点 u，我们找不到一条从它出发的增广路，这时我们只能获得一条交替路。我们把 X集中在交替路的点集叫做 S， X集中不在交替路的点集叫做 S'，同理 Y集中在交替路的点集叫做 T， Y集中不在交替路的点集叫做 T'。如果我们把交替路中 X 集顶点的顶标(点集S中的点)全都减小某个值 d，Y集的顶标(点集T中的点)全都增加同一个值 d，那么我们会发现：
- 两端都在交替路中的边 (e(i ightarrow j))，(l_{i} + l_{j}) 的值没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。
- 两端都不在交替路中的边 (e(i ightarrow j))，(l_{i}, l_{j}) 都没有变化，(l_{i} + l_{j}) 的值没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。
- X集一端在 S' 中， Y端在 T中的边 (e(i ightarrow j))，它的 (l_{i})不变, (l_{j})增加了d，(l_{i} + l_{j})的值有所增大。它原来不属于相等子图，现在仍不可能属于相等子图。
- X集一端在 S中，Y 端在 T'中的边(e(i ightarrow j))，它的 (l_{i})减小了d, (l_{j})不变，(l_{i} + l_{j})的值有所减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。
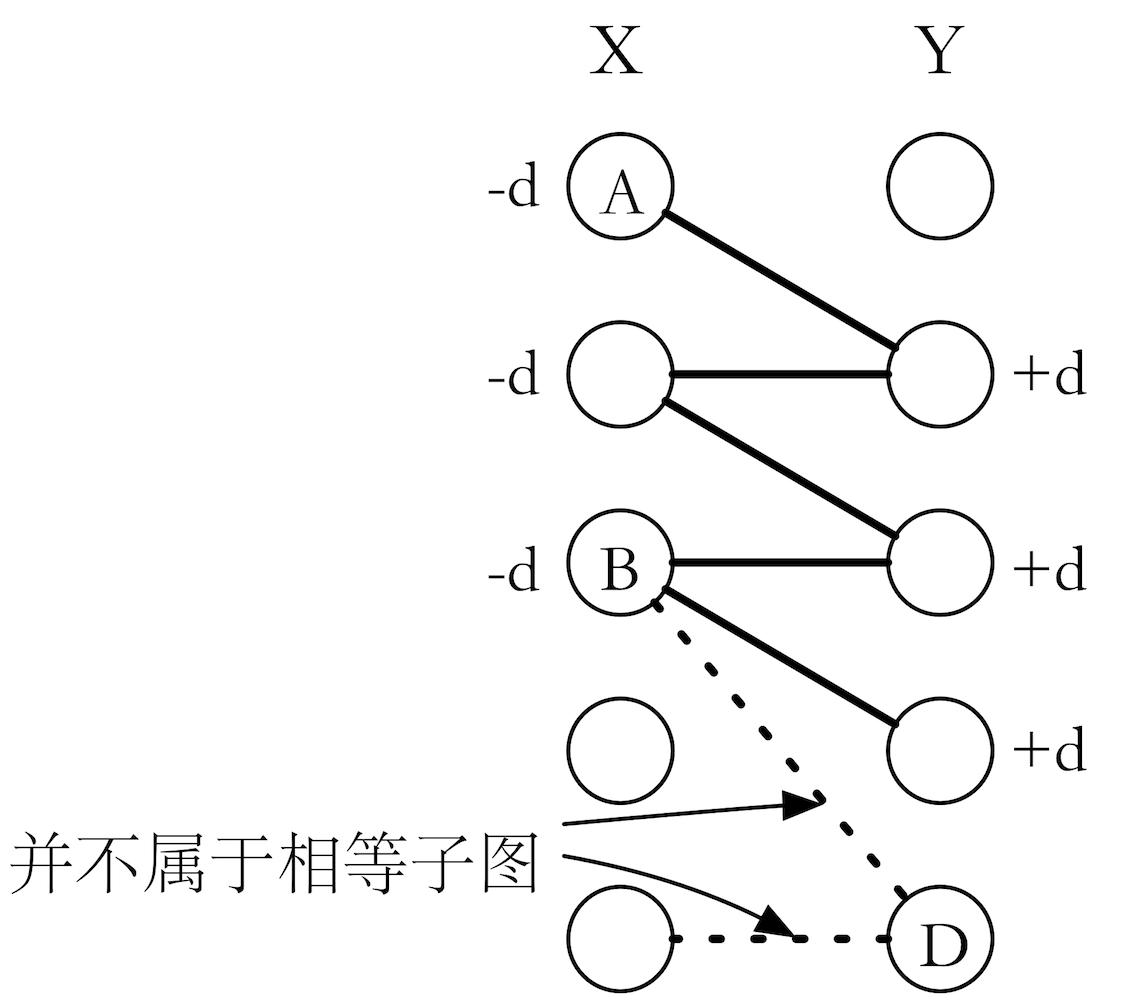
也就是说，只有 X集一端在 S 中，Y端在 T'中的边才有可能被选中。继续贪心，我们只能让满足条件的边权最大的边被选中，即满足(l_{x} + l_{y} = W_{e})，那么这个 d 值，就应该取 (d = min{l_{x} + l_{y} - W_{e(x ightarrow y)} vert x in S, y in T'})。

于是有新的边加入相等子图，我们可以愉快的继续对于未匹配顶点 u寻找增广路，这样的修改最多进行n次，而一共有 n个点，所以除去修改顶标的时间，复杂度已经达到(O(n^{2}))。因此算法的复杂度主要取决于修改顶标的时间, 修改顶标主要两个思路：
- 思路一：枚举所有(n^{2})条边，看是否满足条件，满足条件就更新d值。最直观清晰，然而总的复杂度飙升至(O(n^{4}))。
- 思路二：对于T'的每个点v，定义松弛变量(slack(v) = min{l_{x}+l_{y} -W_{e(x ightarrow y)} vert xin S})，这个松弛变量在匹配的过程中就可以更新，修改顶标的过程中(d = min{slack(v) vert v in T'})。总复杂度(O(n^{3}))，但不是严格的（想一想为什么）?
3.3 KM算法步骤总结

KM算法仅仅只适用于找二分图最佳完美匹配，如果无完美匹配，那么算法很可能陷入死循环（如果不存在的边为 -INF 的话就不会，但正确性就无法保证了），对于这种情况要小心处理。
最后回顾一下总的流程，理一下思路：
1. 初始化可行顶标。
2. 用增广路定理寻对每个点找匹配。
3. 若点未找到匹配则修改可行顶标的值。
4. 重复2、3步直到所有点均有匹配为止，即找到相等子图的完美匹配为止
3.4 KM代码实现

3.4.1 python实现

(O(n^{4}))版本：
```
# Kuhn-Munkres匹配算法, O(n^4)时间复杂度
class KMMatchOriginal(object):

    def __init__(self, graph):
        assert isinstance(graph, np.ndarray), print("二分图的必须采用numpy array 格式")
        assert graph.ndim == 2, print("二分图的维度必须为2")
        self.graph = graph

        rows, cols = graph.shape
        self.rows = rows
        self.cols = cols

        self.lx = np.zeros(self.cols, dtype=np.float32)  # 横向结点的顶标
        self.ly = np.zeros(self.rows, dtype=np.float32)  # 竖向结点的顶标

        self.match_index = np.ones(cols, dtype=np.int32) * -1  # 横向结点匹配的竖向结点的index （默认-1，表示未匹配任何竖向结点）
        self.match_weight = 0  # 匹配边的权值之和

    def match(self):
        # 初始化顶标, ly初始化为0，lx初始化为节点对应权值最大边的权值
        for y in range(self.rows):
            self.ly[y] = max(self.graph[y, :])

        for y in range(self.rows):  # 从每一竖向结点开始，寻找增广路
            while True:
                self.vx = np.zeros(self.cols, dtype=np.int32)  # 横向结点的匹配标志
                self.vy = np.zeros(self.rows, dtype=np.int32)  # 竖向结点的匹配标志
                if self.dfs(y):
                    break
                else:
                    self.update()
        return self.match_index

    # 更新顶标
    def update(self):
        d = np.inf
        # 寻找y中已匹配，x中未匹配，对应需要减小的最小权值
        for y in range(self.rows):
            if self.vy[y]:
                for x in range(self.cols):
                    if not self.vx[x]:
                        d = min(d, self.lx[x] + self.ly[y] - self.graph[y][x])

        for x in range(self.cols):  # x顶标初始化值为0，因此所有匹配点顶标+d
            if self.vx[x]:
                self.lx[x] += d
        for y in range(self.rows):  # y顶标初始化值为对应边的最大权值，因此所有匹配点顶标-d
            if self.vy[y]:
                self.ly[y] -= d

    def dfs(self, y):  # 递归版深度优先搜索
        self.vy[y] = 1
        for x in range(self.cols):
            if self.vx[x] == 0 and self.lx[x] + self.ly[y] == self.graph[y][x]:
                self.vx[x] = 1
                # 两种情况：一是结点x没有匹配，那么找到一条增广路；二是X结点已经匹配，采用DFS，沿着X继续往下走，最后若以未匹配点结束，则也是一条增广路
                if self.match_index[x] == -1 or self.dfs(self.match_index[x]):
                    self.match_index[x] = y  # 未匹配边变成匹配边
                    return True
        return False
if __name__ == '__main__':
    graph = np.array([[2,1,1],[3,2,1],[1,1,1]])
    kmo = KMMatchOriginal(graph)
    print(kmo.match())
```
(O(n^{3}))版本:
```
# Kuhn-Munkres匹配算法
class KMMatch(object):

    def __init__(self, graph):
        assert isinstance(graph, np.ndarray), print("二分图的必须采用numpy array 格式")
        assert graph.ndim == 2, print("二分图的维度必须为2")
        self.graph = graph

        rows, cols = graph.shape
        self.rows = rows
        self.cols = cols

        self.lx = np.zeros(self.cols, dtype=np.float32)  # 横向结点的顶标
        self.ly = np.zeros(self.rows, dtype=np.float32)  # 竖向结点的顶标

        self.match_index = np.ones(cols, dtype=np.int32) * -1  # 横向结点匹配的竖向结点的index （默认-1，表示未匹配任何竖向结点）
        self.match_weight = 0  # 匹配边的权值之和

        self.inc = math.inf

    def match(self):
        # 初始化顶标, lx初始化为0，ly初始化为节点对应权值最大边的权值
        for y in range(self.rows):
            self.ly[y] = max(self.graph[y, :])

        for y in range(self.rows):  # 从每一竖向结点开始，寻找增广路
            while True:
                self.inc = np.inf
                self.vx = np.zeros(self.cols, dtype=np.int32)  # 横向结点的匹配标志
                self.vy = np.zeros(self.rows, dtype=np.int32)  # 竖向结点的匹配标志
                if self.dfs(y):
                    break
                else:
                    self.update()
                # print(y, self.lx, self.ly, self.vx, self.vy)
        return self.match_index

    # 更新顶标
    def update(self):
        for x in range(self.cols):
            if self.vx[x]:
                self.lx[x] += self.inc
        for y in range(self.rows):
            if self.vy[y]:
                self.ly[y] -= self.inc

    def dfs(self, y):  # 递归版深度优先搜索
        self.vy[y] = 1
        for x in range(self.cols):
            if self.vx[x] == 0:
                t = self.lx[x] + self.ly[y] - self.graph[y][x]
                if t == 0:
                    self.vx[x] = 1
                    # 两种情况：一是结点x没有匹配，那么找到一条增广路；二是X结点已经匹配，采用DFS，沿着X继续往下走，最后若以未匹配点结束，则也是一条增广路
                    if self.match_index[x] == -1 or self.dfs(self.match_index[x]):
                        self.match_index[x] = y  # 未匹配边变成匹配边
                        # print(y, x, self.match_index)
                        return True
                else:
                    if self.inc > t:
                        self.inc = t
        return False
if __name__ == '__main__':
    graph = np.array([[2, 1, 1], [3, 2, 1], [1, 1, 1]])
    # # graph = np.array([[3,4,6,4,9],[6,4,5,3,8],[7,5,3,4,2],[6,3,2,2,5],[8,4,5,4,7]])
    km = KMMatch(graph)
    print(km.match())
```
在代码撰写过程中，踩了几个坑，也发现了一些问题，总结如下：
- 在初始化顶标时，若行结点初始化为最大边权值，列结点初始化为0，则必须从行结点出发，遍历寻找满足条件的增广路，否则代码会陷入死循环。（即从初始化为最大边权值的结点开始遍历）
- KM算法要求行结点和列结点个数相同，如果不相同时，保证行结点个数少，列结点个数多，然后通过padding来使行结点和列结点个数相同。
- KM算法求最大权值匹配，若要求最小权值匹配，可以对权值矩阵进行转换，如采用一个很大值(如sys.maxint)减去权值矩阵
3.4.2 cpp代码实现

(O(n^{4}))版本：
```
int Weight[maxm][maxn];
int Lx[maxm], Ly[maxn]; // 顶标
int match[maxn];    // 记录匹配
bool S[maxm], T[maxn];  // 算法中的两个集合S和T

// 步骤 1: 初始化可行顶标和初始化匹配
void Init()
{
    // 将X集合的顶标设为最大边权，Y集合的顶标设为0
    for (int i = 1; i <= m; i++)
    {
        Lx[i] = 0;
        for (int j = 1; j <= n; j++)
        {
            match[j] = 0;   // match记录的是Y集合里的点与谁匹配
            Ly[j] = 0;
            Lx[i] = max(Lx[i], Weight[i][j]);
        }
    }
}
//步骤2：增广路定理寻找匹配点(匈牙利算法中的DFS)
bool findPath(int i)
{
    S[i] = true;
    for (int j = 1; j <= n; j++)
    {
        if (Lx[i] + Ly[j] == Weight[i][j] && !T[j]) // 找出在相等子图里又还未被标记的边
        {
            T[j] = true;
            if (!match[j] || findPath(match[j])) // 未被匹配，或者已经匹配又找到增广路
            {
                match[j] = i;
                return true;
            }
        }
    }
    return false;
}

//步骤 3: 更新顶标
void update() 
{
    // 计算a
    int a = 1 << 30;
    for (int i = 1; i <= m; i++)
        if (S[i])
            for (int j = 1; j <= n; j++)
                if (!T[j])
                    a = min(a, Lx[i] + Ly[j] - Weight[i][j]);

    // 修改顶标
    for (int i = 1; i <= m; i++)
        if (S[i])
            Lx[i] -= a;
    for (int j = 1; j <= n; j++)
        if (T[j]) 
            Ly[j] += a;
}
// 整体的KM算法
void KM()
{
    Init();

    for (int i = 1; i <= m; i++)
    {
        while (true)
        {
            for (int i = 1; i <= m; i++)
                S[i] = 0;
            for (int j = 1; j <= n; j++)
                T[j] = 0;
            if (!findPath(i))
                update();
            else
                break;
        }
    }
}
```
(O(n^{3}))版本：
```
const int maxn = 500 + 3, INF = 0x3f3f3f3f;
int n, W[maxn][maxn];
int mat[maxn];
int Lx[maxn], Ly[maxn], slack[maxn];
bool S[maxn], T[maxn];

inline void tension(int &a, const int b) {
    if(b < a) a = b;
}

inline bool match(int u) {
    S[u] = true;
    for(int v = 0; v < n; ++v) {
        if(T[v]) continue;
        int t = Lx[u] + Ly[v] - W[u][v];
        if(!t) {
            T[v] = true;
            if(mat[v] == -1 || match(mat[v])) {
                mat[v] = u;
                return true;
            }
        }else tension(slack[v], t);
    }
    return false;
}

inline void update() {
    int d = INF;
    for(int i = 0; i < n; ++i)
        if(!T[i]) tension(d, slack[i]);
    for(int i = 0; i < n; ++i) {
        if(S[i]) Lx[i] -= d;
        if(T[i]) Ly[i] += d;
    }
}

inline void KM() {
    for(int i = 0; i < n; ++i) {
        Lx[i] = Ly[i] = 0; mat[i] = -1;
        for(int j = 0; j < n; ++j) Lx[i] = max(Lx[i], W[i][j]);
    }
    for(int i = 0; i < n; ++i) {
        fill(slack, slack + n, INF);
        while(true) {
            for(int j = 0; j < n; ++j) S[j] = T[j] = false;
            if(match(i)) break;
            else update();
        }
    }
}
```
参考：https://nymrli.top/2019/12/05/KM-Kuhn-Munkres-算法/

https://piggerzzm.github.io/2020/03/28/Kuhn-Munkres/

https://www.cnblogs.com/xingnie/p/10395788.html

4. Kuhn-Munkres算法开源包

在实际项目中涉及到最大权值匹配问题时，可以采用开源包中的Kuhn-Munkres算法，如下面两个：

munkres

python有实现了munkres算法的安装包，可以直接安装：pip install munkres

官方使用文档:https://software.clapper.org/munkres/

scipy

scipy模块中scipy.optimize.linear_sum_assignment实现了KM匹配算法，可以直接调用。
相关阅读:
231. Power of Two
204. Count Primes
205. Isomorphic Strings
203. Remove Linked List Elements
179. Largest Number
922. Sort Array By Parity II
350. Intersection of Two Arrays II
242. Valid Anagram
164. Maximum Gap
147. Insertion Sort List
原文地址：https://www.cnblogs.com/silence-cho/p/15112326.html

匈牙利匹配和最大权值匹配算法

1. 基础概念

1.1 二分图

1.2 二分图匹配

1.3 二分图最大匹配

1.4 二分图最大权完美匹配

2. 匈牙利匹配算法

2.1 匈牙利算法解析

2.2 匈牙利算法代码实现

3. KM算法(Kuhn-Munkres Algorithm)

3.1 可行顶标和相等子图

3.2 KM算法步骤解析

3.3 KM算法步骤总结

3.4 KM代码实现

3.4.1 python实现

3.4.2 cpp代码实现

4. Kuhn-Munkres算法开源包