题目描述
你需要构造一棵至少有两个顶点的树,树上的每条边有一个非负整数边权。树上两点 i,j 的距离dis(i,j) 定义为树上连接i 和j 这两点的简单路径上的边权和。
我们定义这棵树的直径为,所有满足 1≤i<j≤n 的 (i,j) 中, dis(i,j) 最大的。如果有多个这样的 (i,j),那么均为直径。
你需要构造一个恰有 k 个直径的树。可以证明在给定的限制下一定有解。
你构造的树需要保证 2≤n≤5000,且每条边的边权满足 50≤w≤10^5。
对于所有数据,满足 1≤k≤5000000。
Solution
构造题真是有意思…[然而本蒟蒻不会x]
构造一棵挂了三个菊花的图…
大概长这样?
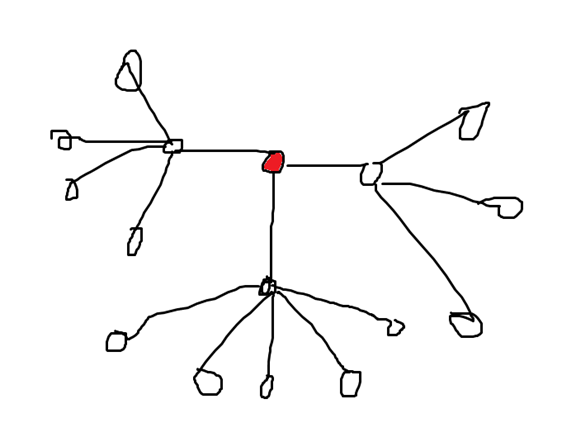
我图画的还是好丑啊
我们要干一件事情我们使得每个菊花图内的每一个分叉都能和另一个菊花的任意一个分叉形成一条直径
这时候我们设左边那棵菊花的节点数为a,下面那棵的节点数为b,右边那棵的节点数为c
那么这个图的直径的数量就是ab+bc+ac
然后我们感性理解打表一下发现,a,b,c最大为1500的时候,就可以做出K的所有情况。
我好菜啊都不会构造
Code
-
#include <bits/stdc++.h>
-
using namespace std;
-
int a,b,c,K;
-
int main()
-
{
-
freopen("diameter.in","r",stdin);
-
freopen("diameter.out","w",stdout);
-
scanf("%d",&K);
-
for (a=1;a<=1500;a++)
-
for (b=a;b<=1500;b++)
-
for (c=b;c<=1500;c++)
-
if (a*b*1ll+b*c*1ll+a*c*1ll==K)
-
goto sinian;
-
a=b=c=-2;
-
sinian:
-
if (a==-2||K<=2000)
-
{
-
printf("%d ",K+1);
-
printf("1 2 2 ");
-
for (int i=2;i<=K;i++)
-
printf("%d %d 0 ",i,i+1);
-
}
-
else
-
{
-
printf("%d ",a+b+c+1);
-
printf("1 2 6666 ");
-
printf("1 3 6666 ");
-
printf("1 4 6666 ");
-
--a;--b;--c;
-
for (int i=5;i<a+5;i++)
-
printf("2 %d 0 ",i);
-
for (int i=a+5;i<a+b+5;i++)
-
printf("3 %d 0 ",i);
-
for (int i=a+b+5;i<a+b+c+5;i++)
-
printf("4 %d 0 ",i);
-
}
-
return 0;
-
}