难度并不NOIP的NOIP模拟赛

　　今天老师请了前几届的学长来讲课，可是讲课为什么要考试呢...

　　学长说难度是NOIP，于是我就naive的跟着参加了，然而T3难度并不友好，感觉确实不是很适合我们现在做......不过课本来也不是给我们这一届讲的？好像逻辑非常自洽的样子。

　　T1：签到题

　　题意概述：从一个长度为n的序列中选出一个长度为k的子序列，使得子序列的字典序最大。$n<=1.5*10^7,k<=10^6$

　　本来想的是一个二维的dp，然而数组开不下，这时候我看向了题目名称：“签到题”，并没有意识到出题人的用意的我坚信这是一道简单题，就真的想出来了...

　　因为字典序是从前往后比较，如果一个数大后面的就不用再比了，有种贪心的感觉，如果一个数大，就一直往前放，这样不就可以了吗？维护一个单调栈，按照顺序往里面加数，不过还要考虑一个问题，如果这个数虽然非常大，但是太靠后了以至于把它作为第一个后面就无法选出k个数了，那不就....但是还是非常好改的，根据每一个点后面有几个点处理出它最早能插入到哪里就好了。(这个问题竟然是对拍才发现的qwq

　　

# include <cstdio>
# include <iostream>
# define R register int

using namespace std;

int Top,x,y,z,n,k;
int a[15000009];
int q[1000009];

void ins (int x)
{
    while (Top>0&&q[Top]<a[x]&&n-x>=k-Top) Top--;
    q[++Top]=a[x];
}

int main()
{
    freopen("red.in","r",stdin);
    freopen("red.out","w",stdout);
    
    scanf("%d%d%d%d%d",&x,&y,&z,&n,&k);
    a[1]=x;
    for (R i=2;i<=n;++i)
        a[i]=(long long)a[i-1]*y%z+1;
    for (R i=1;i<=n;++i)
        ins(i);
    for (R i=1;i<=k;++i)
        printf("%d
",q[i]);

    fclose(stdin);
    fclose(stdout);
    return 0;
}

　　T2:送分题

　　题意概述：在一个n*m的矩阵中有一些障碍，从(1,1)出发到(n,m)，每次只能往下往右走且不能走到障碍上，选出两条这样的不相交路径，求方案数。(n,m<=5000)

　　设$dp[i][j][k]$表示第一条路径进行到(i,j)，第二条进行到(k,i+j-k)时的方案数，随便转移一下即可，但是这样只能过n,m<=300的60分，考场上没有想到正解，后来听了题解感觉非常巧妙。

　　

# include <cstdio>
# include <iostream>
# define mod 1000000007
# define R register int

using namespace std;

int n,m,d,x;
int g[5005][5005];
int dp[305][305][305];

int main()
{
    freopen("sun.in","r",stdin);
    freopen("sun.out","w",stdout);

    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;++i)
        for (int j=1;j<=m;++j)
        {
            scanf("%1d",&x);
            g[i][j]=x; 
        }
    dp[1][1][1]=1;
    for (R a=1;a<=n;++a)
        for (R b=1;b<=m;++b)
            for (R c=a;c<=n;++c)
            {
                x=0;
                d=a+b-c;
                if(d<1||d>m) continue;
                if(g[a][b]||g[c][d]) continue;
                if(a==c&&b==d&&((a==n&&b==m&&c==n)==false)) continue;
                if(a-1!=c-1||b!=d||(a-1==1&&b==1&&c-1==1)) x=(x+dp[a-1][b][c-1])%mod;
                if(a-1!=c||b!=d-1||(a-1==1&&b==1&&c==1)) x=(x+dp[a-1][b][c])%mod;
                if(a!=c-1||b-1!=d||(a==1&&b-1==1&&c-1==1)) x=(x+dp[a][b-1][c-1])%mod;
                if(a!=c||b-1!=d-1||(a==1&&b-1==1&&c==1)) x=(x+dp[a][b-1][c])%mod;
                dp[a][b][c]=(dp[a][b][c]+x)%mod;
            }
    printf("%d",dp[n][m][n]);
    fclose(stdin);
    fclose(stdout);
    return 0;
}

 　　

　　T3:水题

　　感觉题目的名字都非常神奇呢...

　　题意概述：(n,x<=10^6) 对于60%的数据 (n<=100,x<=10^6)

　　

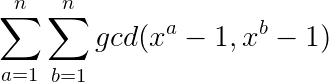
　　答案对1000000007取模。

　　感觉不大好做，就打了一个表找规律，结果还真的有规律，发现每个gcd的值都是$x^k-1$，但是这个k看起来不是很有规律，又打了一个更大的表，发现$k=gcd(a,b)$，于是就用快速幂预处理一下x的幂，$N^2logN$求出答案。这样只有60分，但是我也没有别的办法了。

　　

# include <cstdio>
# include <iostream>
# define mod 1000000007
# define R register int

using namespace std;

int T;
int n,x;
long long ans=0;
long long p[10009];

int gcd (int a,int b)
{
    return b?gcd(b,a%b):a;
}

int main()
{
    freopen("mrazer.in","r",stdin);
    freopen("mrazer.out","w",stdout);
    
    scanf("%d",&T);
    while (T--)
    {
        ans=0LL;
        scanf("%d%d",&x,&n);
        p[0]=1LL;
        for (R i=1;i<=n;++i)
            p[i]=p[i-1]*x%mod;
        for (R i=1;i<=n;++i)
            for (R j=1;j<=n;++j)
                ans=(ans+p[gcd(i,j)]-1)%mod;
        printf("%lld
",ans);
    }
    fclose(stdin);
    fclose(stdout);
    return 0;
}

　　

　　T2的真实做法：

　　为了防止重复，我们钦定第一条路永远在第二条的上面，所以可以认为第一条的起点是(1,2)，终点是(n-1,m),第二条的则是(2,1)，(n,m-1),两种路径的总数$n^2$就可以算，乘法原理再乘起来，这样就是不考虑相交的情况了。

相交情况的分析非常有趣。如果一条路起点是(1,2)，终点是(n,m-1)，另一条起点是(2,1)终点是(n,m-1)，那就肯定相交了，但是既然已经钦定过了，怎么会出现这种情况呢...?所以我们拿出两条不合法的路径来看一看怎么转化。

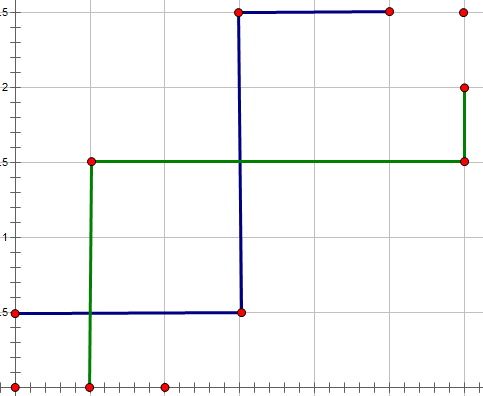
这两条路线显然是不合法的，但是它们并不满足刚刚说的不合法条件，没有关系，我们来转化一下。

　

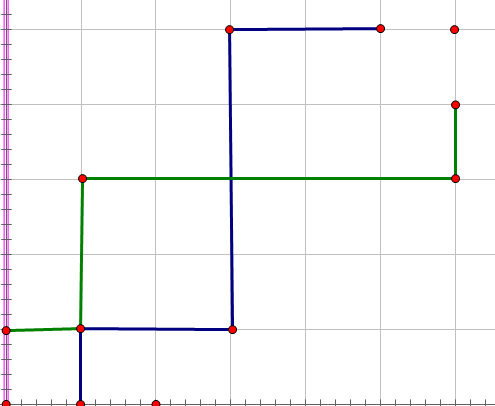
　　把两条不合法路径最后一次相交的点找出来，并且对调两条路径从这里往后的部分，就成了那种之前说的不合法情况了，而且这个变化是可逆的，也就是说，每一种不合法路径都有与之唯一对应的"不合法情况"，所以再$n^2$处理这样的路径总数，用总方案数减去即可。

　　T3的真正做法：

　　莫比乌斯反演，线性筛欧拉函数，最后...NOIP难度。

　　先解释一下打表找规律的正确性，学了辗转相除gcd之后也不要忘了最简单的更相减损术呢。

　　

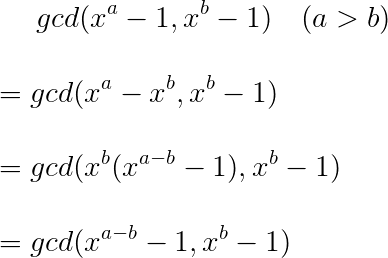
　　第三步是怎么推到第四步的呢？因为$gcd(x^k,x^k-1)=1$，又因为$gcd(a*c,b)=gcd(a,b) (gcd(b,c)=1)$这个结论在某一篇讲斐波那契公因数的blog里证明过。

　　对于指数接着用更相减损术就证出来了。(还是打表找规律好)

　　100分做法我也不会呀，抄抄题解先存在这里以后再看吧。

　　

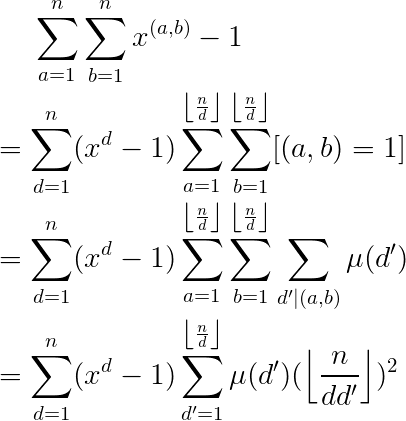
　　不要问我$d'$是什么，我也不知道。

　　

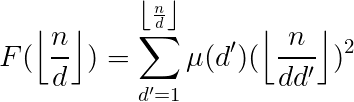
　　这一段可以直接复制真开心。

　　对每个 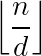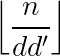， 只有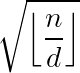 种取值。预处理$F$的复杂度是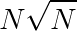,单次回答询问时对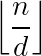分段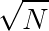，单次回答询问。时间复杂度$O(Nsqrt{N}+Tsqrt{N})$也可以不预处理,每次直接算F,时间复杂度$O(TN^{frac{4}{3}})$

　　这都是些什么啊（小声

　　优化预处理F的复杂度。

　　

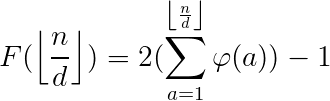
　　求欧拉函数的前缀和。

　　时间复杂度为：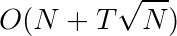

　　再过几年才能看懂这些呢...?

　　没想到我又回来了！今天是2019.1.22，烜神仙从我的blog里面又把这个题翻出来了，重新想了一下，发现没有之前认为的那么难。

　　回顾一下这篇文章的历史，考这套题的时候我还什么都不会，但是联赛后我就学习了反演，终于会做这道题了，甚至还找到了比之前更好想的一种做法。

　　下面让我们从之前咕掉的部分：更相减损术接上来，因为那一段好像已经很明白了。

　　$sum_{i=1}^nsum_{j=1}^nx^{(i,j)}-1$

　　$sum_{i=1}^nsum_{j=1}^nx^{(i,j)}-n^2$

　　接下来就都是一些套路了

　　$sum_{d=1}^nx^dsum_{i=1}^nsum_{j=1}^n[(i,j)==d]$

　　$sum_{d=1}^nx^dsum_{i=1}^{n/d}sum_{j=1}^{n/d}[(i,j)==1]$

　　看到 $gcd$ ，就可以请出莫反的常见套路了。

　　$sum_{d=1}^nx^dsum_{i=1}^{n/d}sum_{j=1}^{n/d}sum_{k|i,k|j}mu(k)$

　　$sum_{d=1}^nx^dsum_{k=1}^nmu(k)(frac{n}{kd})^2$

　　接下来，可以按照莫反的套路一路化下去，最终会有这个式子：

　　$sum_{d=1}^n(frac{n}{d})^2sum_{i|d}mu(frac{d}{i})x^i$

　　这之后会很难办，可以杜教筛，但是比较麻烦。

　　讲这个故事就是为了说明：套路固然很重要，但是如果只有套路，就会显得很不真诚，如果没有一种真诚的做题的态度，那对于不套路的题就很可能做不出来啦。

　　跳回几步，回到之前的式子：

　　$sum_{d=1}^nx^dsum_{i=1}^{n/d}sum_{j=1}^{n/d}[(i,j)==1]$

　　把后面一部分提出来：

　　$sum_{i=1}^{n/d}sum_{j=1}^{n/d}[(i,j)==1]$

　　改一下：

　　$sum_{i=1}^{n}sum_{j=1}^{n}[(i,j)==1]$

　　回忆一下学莫比乌斯反演的时候，做过的一些入门题目：

　　$sum_{i=1}^nsum_{j=1}^m[(i,j)==1]$

　　之所以这种题目里要引进莫比乌斯函数，是因为两个和式的上标不一样。如果一样的话，完全可以用欧拉函数来做，再一次回到原来的式子：

　　$sum_{i=1}^{n}sum_{j=1}^{n}[(i,j)==1]=sum_{i=1}^nsum_{j=1}^i varphi(i) imes 2-1$

　　形象化的说，一开始求的是一个矩阵的下半三角。（i>=j)

　　

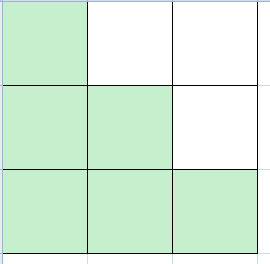
　　乘二是将它的对称部分也求出来。

　　 

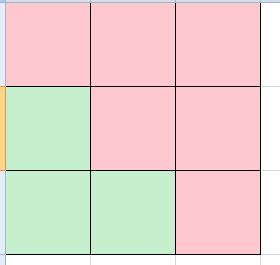
 　　最后减掉算了两次的（1，1）这个数对，就是所需答案。

　　

# include <cstdio>
# include <iostream>
# define R register int
# define mod 1000000007
# define ll long long

using namespace std;

const int maxn=1000006;
int T,X[maxn],N[maxn],maxx,x,n,phi[maxn],vis[maxn],pri[maxn],h;
ll ans;

inline int read()
{
    R x=0;
    char c=getchar();
    while (!isdigit(c)) c=getchar();
    while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x;
}

inline void init (int n)
{
    phi[1]=1;
    for (R i=2;i<=n;++i)
    {
        if(!vis[i]) pri[++h]=i,phi[i]=i-1;
        for (R j=1;j<=h&&i*pri[j]<=n;++j)
        {
            vis[ i*pri[j] ]=true;
            if(i%pri[j]==0)
            {
                phi[ i*pri[j] ]=1LL*phi[i]*pri[j]%mod;
                break;
            }
            phi[ i*pri[j] ]=1LL*phi[i]*(pri[j]-1)%mod;
        }
    }
    for (R i=2;i<=n;++i) phi[i]=(2LL*phi[i]+phi[i-1])%mod;
}

inline ll qui (int a,int b)
{
    ll s=1;
    while(b)
    {
        if(b&1) s=s*a%mod;
        a=1LL*a*a%mod;
        b>>=1;
    }
    return s;
}

inline int db (int x,int a,int b)
{
    if(x==1) return (b-a+1);
    return (1LL*qui(x,a)*(1-qui(x,b-a+1)+mod)%mod*qui(1-x+mod,mod-2)%mod+mod)%mod;
}

int main()
{
    T=read();
    for (R i=1;i<=T;++i) X[i]=read(),N[i]=read(),maxx=max(maxx,N[i]);
    init(maxx);
    for (R t=1;t<=T;++t)
    {
        x=X[t],n=N[t],ans=0;
        int i=1,l;
        while(i<=n)
        {
            l=n/(n/i);
            ans=((ans+1LL*phi[n/i]*db(x,i,l))%mod+mod)%mod;
            i=l+1;
        }
        printf("%lld
",((ans-1LL*n*n)%mod+mod)%mod);
    }
    return 0;
}

 　---shzr