用python计算圆周率Π

一、要求：

1.计算到圆周率后面越多位越好。

2.用进度条显示计算的进度。

3.要求给出圆周率Π的具体计算方法和解释。

二、算法：

1.拉马努金公式：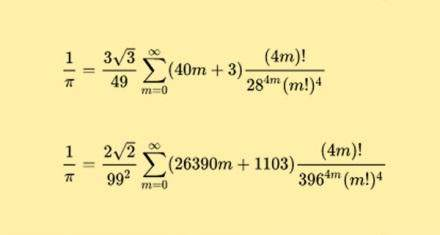

2.高斯-勒让德公式：

设置初始值：

反复执行以下步骤直到

  

与

 

之间的误差到达所需精度：

则π的近似值为：

下面给出前三个迭代结果（近似值精确到第一个错误的位数）：

3.140...

3.14159264...

3.1415926535897932382...

该算法具有二阶收敛性，本质上说就是算法每执行一步正确位数就会加倍。

3.波尔文四次迭代式

这个公式由乔纳森·波尔文和彼得·波尔文于1985年发表的。

bailey-borwein-plouffe算法

这个公式简称BBP公式，由David Bailey, Peter Borwein和Simon Plouffe于1995年共同发表。它打破了传统的圆周率的算法，可以计算圆周率的任意第n位，而不用计算前面的n-1位。这为圆周率的分布式计算提供了可行性。

4.丘德诺夫斯基公式

这是由丘德诺夫斯基兄弟发现的，十分适合计算机编程，是目前计算机使用较快的一个公式。

5.莱布尼茨公式

π/4=1-1/3+1/5-1/7+1/9-1/11+……

6.蒙特卡罗法（打鸟法）

一个正方形内部相切一个圆，圆和正方形的面积之比是π/4。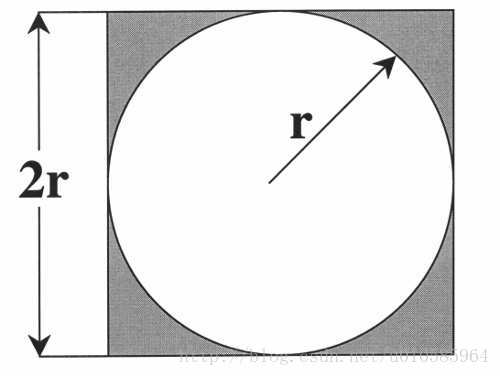 
 
在这个正方形内部，随机产生n个点（这些点服从均匀分布），计算它们与中心点的距离是否大于圆的半径，以此判断是否落在圆的内部。

统计圆内的点数，与n的比值乘以4，就是π的值。理论上，n越大，计算的π值越准。

三、算法实现

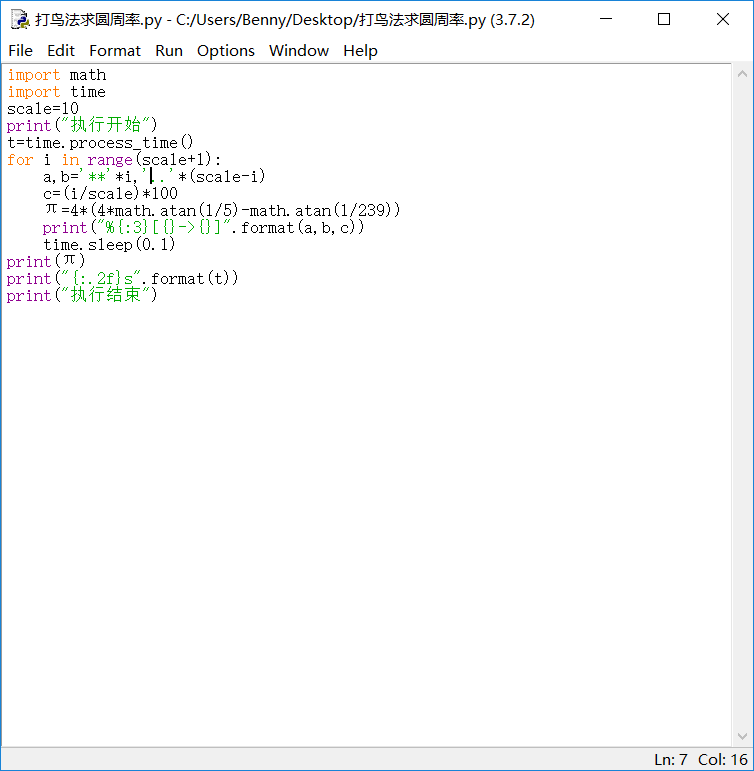
以下采用蒙特卡罗法（打鸟法），代码及图片如下。 

import math
import time
scale=10
print("执行开始")
t=time.process_time()
for i in range(scale+1):
    a,b='**'*i,'..'*(scale-i)
    c=(i/scale)*100
    π=4*(4*math.atan(1/5)-math.atan(1/239))
    print("[{}{}->%{}]".format(a,b,c))
    time.sleep(0.1)
print(π)
print("程序用时：{:.2f}s".format(t))
print("执行结束")

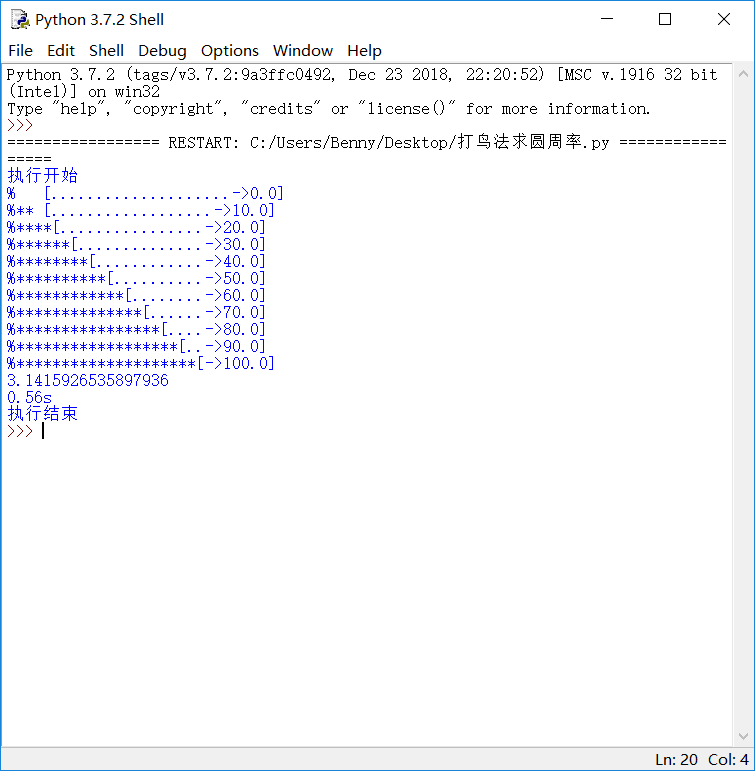
运行结果：

Python 3.7.2 (tags/v3.7.2:9a3ffc0492, Dec 23 2018, 22:20:52) [MSC v.1916 32 bit (Intel)] on win32
Type "help", "copyright", "credits" or "license()" for more information.
>>> 
================= RESTART: C:/Users/Benny/Desktop/打鸟法求圆周率.py =================执行开始
[....................->%0.0]
[**..................->%10.0]
[****................->%20.0]
[******..............->%30.0]
[********............->%40.0]
[**********..........->%50.0]
[************........->%60.0]
[**************......->%70.0]
[****************....->%80.0]
[******************..->%90.0]
[********************->%100.0]
3.1415926535897936
程序用时：0.11s
执行结束
>>> 

另外，进度条还可以用python的pip库来实现：

import mathimport timescale=10print("执行开始")t=time.process_time()for i in range(scale+1):    a,b='**'*i,'..'*(scale-i)    c=(i/scale)*100    π=4*(4*math.atan(1/5)-math.atan(1/239))    print("%{:3}[{}->{}]".format(a,b,c))    time.sleep(0.1)print(π)print("{:.2f}s".format(t))print("执行结束")