A - Add More Zero
题意:
给出m,对于2^m >= 10^k,k最大为多少?
分析:
两边同时开个log10,k = m * log10(2).
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e5+100; int main() { // freopen("in.txt","r",stdin); int n,Case=1; while(scanf("%d",&n)!=EOF) { int ans=n*log10(2); printf("Case #%d: %d ",Case++,ans); } return 0; }
B - Balala Power!
题意:
一个字符串为一个26进制数,现在给其中的字符赋值(0~25),每个值只能对应一个字符,求n个字符串转为十进制后相加的和最大为多少。
分析:
首先考虑一个字符串,对于一个字母如果它所占的权重越大,那么我们就该它赋值越大。对于abca来说,a所占的权重为26^3 + 26^0,b的权重为26^2,c的权重为26^1,所以对于a,b,c分别赋值25,24,23。
对于前导0的情况,我们找到一个赋值最小且没有在字符串第一个出现的字母与之交换赋值。
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxm=26; const int maxn=1e5+100; const int mod=1e9+7; ll ans; int n,Case=1,maxlen; ll mp[200]; bool vis[200]; string s[maxn]; struct Node{ char ch; int weight[maxn]; }; Node node[maxm]; void init() { ans=0; maxlen=0; cls(mp); cls(vis); for(int i=0;i<maxm;i++){ node[i].ch=char('a'+i); cls(node[i].weight); } } bool cmp(Node a,Node b) { for(int i=maxlen;i>=0;i--){ if(a.weight[i]==b.weight[i]) continue; return a.weight[i]>b.weight[i]; } return a.ch<b.ch; } ll poww(ll a,ll k) { ll res=1; while(k) { if(k&1) res=res*a%mod; a=a*a%mod; k>>=1; } return res; } void solve(int id,int pos) { maxlen=max(pos,maxlen); for(int i=pos;i<maxn;i++){ if(node[id].weight[i]<maxm) return; node[id].weight[i+1]++; maxlen=max(i+1,maxlen); node[id].weight[i]%=maxm; } } int main() { // freopen("in.txt","r",stdin); ios::sync_with_stdio(false); while(cin>>n) { init(); for(int i=1;i<=n;i++){ cin>>s[i]; } for(int i=1;i<=n;i++){ int len=s[i].length(); for(int j=len-1;j>=0;j--){ int id=s[i][j]-'a'; node[id].weight[len-1-j]++; solve(id,len-1-j); } vis[s[i][0]]=true; } sort(node,node+maxm,cmp); for(int i=0;i<maxm;i++){ mp[node[i].ch]=25-i; } for(int i=maxm-1;i>=0;i--){ if(mp[node[i].ch]==0&&vis[node[i].ch]==true){ for(int j=i-1;j>=0;j--){ if(mp[node[j].ch]!=0){ mp[node[i].ch]=mp[node[j].ch]; mp[node[j].ch]=0; break; } } } } for(int i=1;i<=n;i++){ int len=s[i].length(); for(int j=len-1;j>=0;j--){ ans=(ans+mp[s[i][j]]*poww(26,len-1-j))%mod; } } cout<<"Case #"<<Case++<<": "<<ans<<endl; } return 0; }
F - Function
参考资料:大佬博客
题意:
给出两个序列,一个是0~n-1的排列a,另一个是0~m-1的排列b,现在求满足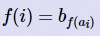 的f的个数。
的f的个数。
分析:
先看一下样例吧:

对于这组数来说,假如我们先指定了f(0)对应的在b中的值,那么根据第2个式子,就可以得出f(1),根据f(1)就又可以得出f(2),最后根据f(2)就可以检验f(0)的值是否正确。这也就是说,对于a中的一个循环节,只要确定了其中一个数所映射的值,那么其它数就都被相应的确定了。

所以我们需要先计算出a和b中的循环节个数和每个循环节对应的个数,然后根据循环节的因子关系就可以判断是否成立。
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int mod=1e9+7; const int maxn=1e6+100; int n,m; int Case=1; int tota,totb; bool vis[maxn]; int a[maxn],b[maxn]; int A[maxn],B[maxn]; void getCycleLen(int* a,int arrayLen,int* A,int& tot) { tot=0; cls(vis); for(int i=0;i<arrayLen;i++){ int index=i,cnt=0; while(!vis[index]) { cnt++; vis[index]=true; index=a[index]; } if(cnt){ A[tot++]=cnt; } } } int main() { // freopen("in.txt","r",stdin); while(scanf("%d%d",&n,&m)!=EOF) { for(int i=0;i<n;i++){ scanf("%d",&a[i]); } for(int i=0;i<m;i++){ scanf("%d",&b[i]); } getCycleLen(a,n,A,tota); getCycleLen(b,m,B,totb); ll ans=1; for(int i=0;i<tota;i++){ ll tmp=0; for(int j=0;j<totb;j++){ if(A[i]%B[j]==0){ tmp=(tmp+B[j])%mod; } } ans=ans*tmp%mod; } printf("Case #%d: %lld ",Case++,ans); } return 0; }
题意:
KazaQ有n双袜子,编号为1~n,每天早上穿一双(每次穿编号最小的),穿过的袜子放在篮子里,如果篮子里的袜子达到n-1双后,KazaQ会洗他穿过的袜子,袜子在第二天晚上放在篮子中,问第k天KazaQ穿的是哪个编号的袜子。
分析:
首先对于前n天,很容易得出穿的袜子编号分别为1,2,3,……,n,n+1天为前n-1天穿过的袜子中编号最小的,n+2天为前n-1天穿过的袜子中编号第二小的……当每次只有一双袜子时,下一天穿的袜子就为这天前面n-1天所穿袜子中编号最小的。
写出数据后,很容易得到数据的循环节为2*(n-1)。
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e5+100; const int mod=1e9+7; ll n,k,Case=1; ll solve(ll k) { if(k<=n) return k; if(k<=n+n-1) return k-n; if(k<n+(n-1)*2) return k-(n+n-1); if(k==n+(n-1)*2) return n; return solve((k-n)%((n-1)*2)+n); } /** 3 7 1 2 3 1 2 1 3 1 2 1 3 3 6 1 2 3 1 2 1 3 1 2 1 3 4 9 1 2 3 4 1 2 3 1 2 4 1 2 3 1 2 4 5 10 1 2 3 4 5 1 2 3 4 1 2 3 5 1 2 3 4 1 2 3 5 */ int main() { // freopen("in.txt","r",stdin); while(scanf("%lld%lld",&n,&k)!=EOF) { printf("Case #%lld: %lld ",Case++,solve(k)); } return 0; }
