题目大意
给出一个区间的长度 N,及 M 个子区间和, 形如:x y z, 表示子区间 [x, y] 的和为 z如果一个“子区间和”与前面的“子区间和”冲突,即为错误(而且这个“子区间和”将在接下来的判断中被忽略)。求总错误个数。
解题思路
当一段子区间和与前面发生冲突是,说明可以从之前的信息中得到这个子区间的值并且两者不一样。那么问题就是怎么从所给信息中确定一个子区间的值了。如果我们可以得到两点之间的值,说明它们有一个共同的公共点,所以就能想到用并查集来解决。比方说我们知道了[1,3]的值和[1,10]的值,那么3和10有一个公共点1,我们就可以根据1来推出[4,10]的值(为什么不是[3,10]?因为都是闭区间,在纸上画画就知道了),假如之后又出现了[4,10]的值且和我们算出来的不一样,那肯定就冲突了。
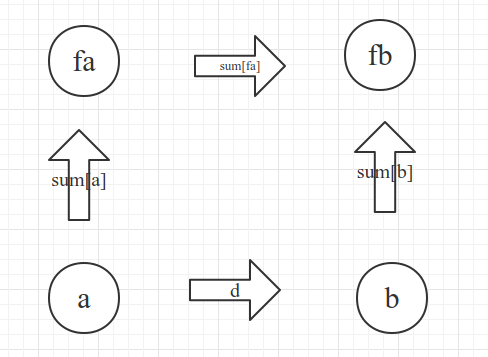
那么如何维护这个并查集呢?我们设sum[x]表示x到根结点的值,那么对于两个点a和b以及他们之间的距离d,我们把a的父节点挂在b的父节点下面,使它们在一个集合之中,因为a到b的距离是d,所以a到b的距离加上b到b的父节点的距离就应该和a到a的父节点的距离加上a的父节点到b的父节点的距离相同。所以我们只要更新一下a的父节点到b的父节点的距离,然后在路径压缩的过程中更新每个点到其父节点的距离就好了。
代码
const int maxn = 2e5+10;
int p[maxn], sum[maxn];
int find(int x) {
if (p[x]!=x) {
int tmp = p[x];
p[x] = find(p[x]);
sum[x] += sum[tmp];
}
return p[x];
}
int main(void) {
int n, m;
while(~scanf("%d%d",&n,&m)) {
for (int i = 0; i<=n; ++i) {
p[i] = i; sum[i] = 0;
}
int cnt = 0;
for (int i = 0,a,b,c; i<m; ++i) {
scanf("%d%d%d",&a,&b,&c);
--a;
int fa = find(a), fb = find(b);
if (fa==fb && sum[a]-sum[b]!=c) ++cnt;
else if (fa!=fb) {
p[fa] = fb;
sum[fa] = sum[b]-sum[a]+c;
}
}
printf("%d
",cnt);
}
return 0;
}