• Dijkstra算法

     

        Dijkstra算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉发明的。算法解决的是有向图中单个源点到其他顶点的最短路径问题。举例来说，如果图中的顶点表示城市，而边上的权重表示着城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

    Dijkstra算法

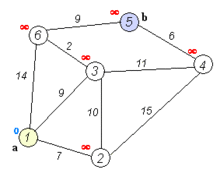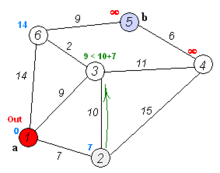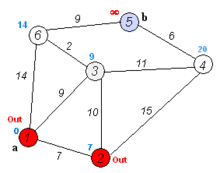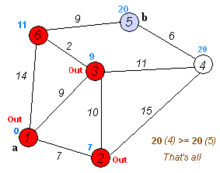
        这个算法是通过每个顶点V保留目前为止所找到的从s到v的最短路劲来工作的。初始时，源点s的路径长度值被赋值为0即d[s] = 0，若存在能直接到达的边(s, m)，则把d[m]设为w(s, m)，同时吧所有其他(s不能直接到达的)顶点的路径长度设为无穷大，即表示我们不知道任何通向这些顶点的路径(对于V中的所有顶点v除s和上述m外d[v] = ∞)。当算法退出时，d[v]中存储的便是从s到v的最短路径，或者路劲不存在，即无穷大。Dijkstra算法的基础操作时边的拓展：如果存在一条从u到v的边，那么从s到v的最短路径可以通过将边(u, v)添加到尾部来拓展一条从s到u的路径。这条路径的长度是d[u] + w(u, v)。如果这个值比目前已知的d[v]的要小，我们可以用新值来替代当前d[v]中的值。拓展边的操作一直运行到所有的d[v]都从s到v最短路径的花费。这个算法经过组织因而当d[u]达到它最终的值的时候每条边(u, v)都只被拓展一次。

        算法的维护两个顶点集S和Q。集合S保留了我们已知的所有d[v]的值已经是最短路径的值顶点，而集合Q则保留其他所有顶点。集合S的初试状态为空，而后每一步都有一个顶点从Q移动到S。这个被选择的顶点是Q中拥有最小的d[u]值的顶点。当一个顶点u从Q中转移到了S中算法对每条外接边(u, v)进行拓展。

        对于时间复杂度，Dijkstra算法最简单的实现方法是用一个链表或者数组来存储所有顶点集合Q，所以搜索Q中最小元素的运算只需要线性搜索Q中的所有元素，这样的话算法的运算时间是O(n2)。对于边数少于n2的稀疏图来说我们可以用链接表来更有效的实现该算法。同时更需要将一个二叉堆或者斐波那契堆作为优先队列来查找最小的顶点。

        下面附上代码：

      1 /*
  2 * about: shortest path(Dijkstra)
  3 * author: zju.dsh
  4 * date: 1/4/2013
  5 */
  6 
  7 #include<stdio.h>
  8 
  9 #define INF 0x7fffffff    //在32为机器上int的最大值
 10 #define max 6
 11 #define BEGIN 0
 12 #define END 5
 13 
 14 int find_minimum_route( int route[], int visit[], int *position, int vertex_number )
 15 {
 16     int i;
 17     int tag = 0;
 18     int temp;
 19     i = 0;
 20     temp = INF;
 21     while( i < vertex_number )
 22     {
 23         if( (temp > route[i]) && (visit[i] == 0) )
 24         {
 25             temp = route[i];
 26             *position = i;
 27             tag = 1;
 28         }
 29         ++i;
 30     }
 31     if( 1 == tag )
 32         return temp;
 33     else
 34     {
 35         *position = vertex_number;
 36         return INF;
 37     }
 38 }
 39 
 40 void Dijkstra( int Graph_list_search[max][max], int first, int end )
 41 {
 42     int i, j, k;
 43     //first点到其余个点的距离
 44     int Graph_minimum_Distance[max];
 45     //判断在S集合中
 46     int Graph_visit[max];
 47     int Graph_minimum_road[max][max];
 48     int position;
 49     int minimum_Distance;
 50 
 51     for( i = 0; i < max; ++i )
 52     {
 53         Graph_minimum_Distance[i] = Graph_list_search[first][i];
 54         Graph_visit[i] = 0;
 55         for( j = 0; j < max; ++j )
 56         {
 57             Graph_minimum_road[i][j] = 0;
 58         }
 59         if( Graph_minimum_Distance[i] < INF )
 60         {
 61             Graph_minimum_road[i][BEGIN] = 1;
 62             Graph_minimum_road[i][i] = 1;
 63         }
 64     }
 65     Graph_minimum_Distance[BEGIN] = 0;
 66     Graph_visit[BEGIN] = 1;
 67     for( i = 1; i < max; ++i )
 68     {
 69         minimum_Distance = find_minimum_route( Graph_minimum_Distance, Graph_visit, &position, max );
 70         Graph_visit[position] = 1;
 71         for( j = 0; j < max; ++j )
 72         {
 73             if( 0 == Graph_visit[j] )
 74             {
 75                 if( Graph_minimum_Distance[j] > 
 76                     minimum_Distance + Graph_list_search[position][j] )
 77                 {
 78                     Graph_minimum_Distance[j] = minimum_Distance + Graph_list_search[position][j];
 79                 }
 80                 for( k = 0; k < max; ++k )
 81                 {
 82                     Graph_minimum_road[j][k] = Graph_minimum_road[position][k];
 83                 }
 84                 Graph_minimum_road[j][j] = 1;
 85             }
 86         }
 87     }
 88     printf( "The minimum road is( vertex%d->vertex%d ):\n",BEGIN, END );
 89     //第一次用到
 90     for( i = 0; i < max && printf("->"); ++i )
 91     {
 92         if( 1 == Graph_minimum_road[end][i] )
 93         {
 94             printf("vertex%d",i);
 95         }
 96     }
 97     printf("\n");
 98 }
 99 
100 void print_edge( int Graph_list_search[max][max] )
101 {
102     printf( "The example edge is:\n" );
103     for( int i = 0; i < max; ++i )
104     {
105         for( int j = 0; j < max; ++j )
106         {
107             if( INF == Graph_list_search[i][j] )
108                 printf("INF\t");
109             else
110                 printf( "%d\t", Graph_list_search[i][j] );
111         }
112         printf("\n");
113     }
114 }
115 
116 int main()
117 {
118     int Graph_list_search[max][max] = {
119         {0, 3, 2, 5, INF, INF},
120         {INF, 0, INF, 2, INF, INF},
121         {INF, INF, 0, 1, INF, INF},
122         {INF, INF, INF, 0, INF, 5},
123         {INF, INF, 5, 3, 0, 1},
124         {INF, INF, INF, INF, INF, 0}
125     };
126     print_edge( Graph_list_search );
127     Dijkstra( Graph_list_search, BEGIN, END );
128     return 0;
129 }

    内容参考过网络资源！！！

    ---恢复内容结束---

     

        Dijkstra算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉发明的。算法解决的是有向图中单个源点到其他顶点的最短路径问题。举例来说，如果图中的顶点表示城市，而边上的权重表示着城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径。

    Dijkstra算法

        这个算法是通过每个顶点V保留目前为止所找到的从s到v的最短路劲来工作的。初始时，源点s的路径长度值被赋值为0即d[s] = 0，若存在能直接到达的边(s, m)，则把d[m]设为w(s, m)，同时吧所有其他(s不能直接到达的)顶点的路径长度设为无穷大，即表示我们不知道任何通向这些顶点的路径(对于V中的所有顶点v除s和上述m外d[v] = ∞)。当算法退出时，d[v]中存储的便是从s到v的最短路径，或者路劲不存在，即无穷大。Dijkstra算法的基础操作时边的拓展：如果存在一条从u到v的边，那么从s到v的最短路径可以通过将边(u, v)添加到尾部来拓展一条从s到u的路径。这条路径的长度是d[u] + w(u, v)。如果这个值比目前已知的d[v]的要小，我们可以用新值来替代当前d[v]中的值。拓展边的操作一直运行到所有的d[v]都从s到v最短路径的花费。这个算法经过组织因而当d[u]达到它最终的值的时候每条边(u, v)都只被拓展一次。

        算法的维护两个顶点集S和Q。集合S保留了我们已知的所有d[v]的值已经是最短路径的值顶点，而集合Q则保留其他所有顶点。集合S的初试状态为空，而后每一步都有一个顶点从Q移动到S。这个被选择的顶点是Q中拥有最小的d[u]值的顶点。当一个顶点u从Q中转移到了S中算法对每条外接边(u, v)进行拓展。

        对于时间复杂度，Dijkstra算法最简单的实现方法是用一个链表或者数组来存储所有顶点集合Q，所以搜索Q中最小元素的运算只需要线性搜索Q中的所有元素，这样的话算法的运算时间是O(n2)。对于边数少于n2的稀疏图来说我们可以用链接表来更有效的实现该算法。同时更需要将一个二叉堆或者斐波那契堆作为优先队列来查找最小的顶点。

        下面附上代码：

      1 /*
  2 * about: shortest path(Dijkstra)
  3 * author: zju.dsh
  4 * date: 1/4/2013
  5 */
  6 
  7 #include<stdio.h>
  8 
  9 #define INF 0x7fffffff    //在32为机器上int的最大值
 10 #define max 6
 11 #define BEGIN 0
 12 #define END 5
 13 
 14 int find_minimum_route( int route[], int visit[], int *position, int vertex_number )
 15 {
 16     int i;
 17     int tag = 0;
 18     int temp;
 19     i = 0;
 20     temp = INF;
 21     while( i < vertex_number )
 22     {
 23         if( (temp > route[i]) && (visit[i] == 0) )
 24         {
 25             temp = route[i];
 26             *position = i;
 27             tag = 1;
 28         }
 29         ++i;
 30     }
 31     if( 1 == tag )
 32         return temp;
 33     else
 34     {
 35         *position = vertex_number;
 36         return INF;
 37     }
 38 }
 39 
 40 void Dijkstra( int Graph_list_search[max][max], int first, int end )
 41 {
 42     int i, j, k;
 43     //first点到其余个点的距离
 44     int Graph_minimum_Distance[max];
 45     //判断在S集合中
 46     int Graph_visit[max];
 47     int Graph_minimum_road[max][max];
 48     int position;
 49     int minimum_Distance;
 50 
 51     for( i = 0; i < max; ++i )
 52     {
 53         Graph_minimum_Distance[i] = Graph_list_search[first][i];
 54         Graph_visit[i] = 0;
 55         for( j = 0; j < max; ++j )
 56         {
 57             Graph_minimum_road[i][j] = 0;
 58         }
 59         if( Graph_minimum_Distance[i] < INF )
 60         {
 61             Graph_minimum_road[i][BEGIN] = 1;
 62             Graph_minimum_road[i][i] = 1;
 63         }
 64     }
 65     Graph_minimum_Distance[BEGIN] = 0;
 66     Graph_visit[BEGIN] = 1;
 67     for( i = 1; i < max; ++i )
 68     {
 69         minimum_Distance = find_minimum_route( Graph_minimum_Distance, Graph_visit, &position, max );
 70         Graph_visit[position] = 1;
 71         for( j = 0; j < max; ++j )
 72         {
 73             if( 0 == Graph_visit[j] )
 74             {
 75                 if( Graph_minimum_Distance[j] > 
 76                     minimum_Distance + Graph_list_search[position][j] )
 77                 {
 78                     Graph_minimum_Distance[j] = minimum_Distance + Graph_list_search[position][j];
 79                 }
 80                 for( k = 0; k < max; ++k )
 81                 {
 82                     Graph_minimum_road[j][k] = Graph_minimum_road[position][k];
 83                 }
 84                 Graph_minimum_road[j][j] = 1;
 85             }
 86         }
 87     }
 88     printf( "The minimum road is( vertex%d->vertex%d ):\n",BEGIN, END );
 89     //第一次用到
 90     for( i = 0; i < max && printf("->"); ++i )
 91     {
 92         if( 1 == Graph_minimum_road[end][i] )
 93         {
 94             printf("vertex%d",i);
 95         }
 96     }
 97     printf("\n");
 98 }
 99 
100 void print_edge( int Graph_list_search[max][max] )
101 {
102     printf( "The example edge is:\n" );
103     for( int i = 0; i < max; ++i )
104     {
105         for( int j = 0; j < max; ++j )
106         {
107             if( INF == Graph_list_search[i][j] )
108                 printf("INF\t");
109             else
110                 printf( "%d\t", Graph_list_search[i][j] );
111         }
112         printf("\n");
113     }
114 }
115 
116 int main()
117 {
118     int Graph_list_search[max][max] = {
119         {0, 3, 2, 5, INF, INF},
120         {INF, 0, INF, 2, INF, INF},
121         {INF, INF, 0, 1, INF, INF},
122         {INF, INF, INF, 0, INF, 5},
123         {INF, INF, 5, 3, 0, 1},
124         {INF, INF, INF, INF, INF, 0}
125     };
126     print_edge( Graph_list_search );
127     Dijkstra( Graph_list_search, BEGIN, END );
128     return 0;
129 }

    内容参考过网络资源！！！
  • 相关阅读:
    在rhel上配置yum 源
    python2.7 使用生成器方式实现斐波那契数列
    Web 应用程序测试思考
    python2.7 可迭代对象、迭代器和迭代的概念说明
    python2.7 zipfile 的简单用法
    python函数定义中的参数说明
    python 内置函数filter、map、reduce的使用说明
    python虚拟环境迁移
    python yaml 文件解析及str、repr函数的说明
    python xlrd、xlwt、xlutils操作excel文件
  • 原文地址：https://www.cnblogs.com/shuanghong/p/2956541.html
Copyright © 2020-2023  润新知