先,定义一下 状态Position P 先手必败 N x先手必胜
操作方法: 反向转移
相同状态 不同位置 的一对 相当于无
对于ICG游戏,我们可以将游戏中每一个可能发生的局面表示为一个点。并且若存在局面i和局面j,且j是i的后继局面(即局面i可以转化为局面j),我们用一条有向边,从i出发到j,连接表示局面i和局面j的点。则整个游戏可以表示成为一个有向无环图:
根据ICG游戏的定义我们知道,任意一个无法继续进行下去的局面为终结局面,即P局面(先手必败)。在上图中我们可以标记所有出度为0的点为P点。接着根据ICG游戏的两条性质,我们可以逆推出所有点为P局面还是N局面:
对于一个游戏可能发生的局面x,我们如下定义它的sg值:
(1)若当前局面x为终结局面,则sg值为0。
(2)若当前局面x非终结局面,其sg值为:sg(x) = mex{sg(y) | y是x的后继局面}。
mex{a[i]}表示a中未出现的最小非负整数。举个例子来说:
mex{0, 1, 2} = 3, mex{1, 2}=0, mex{0,1,3}=2
我们将上图用sg函数表示后,得到: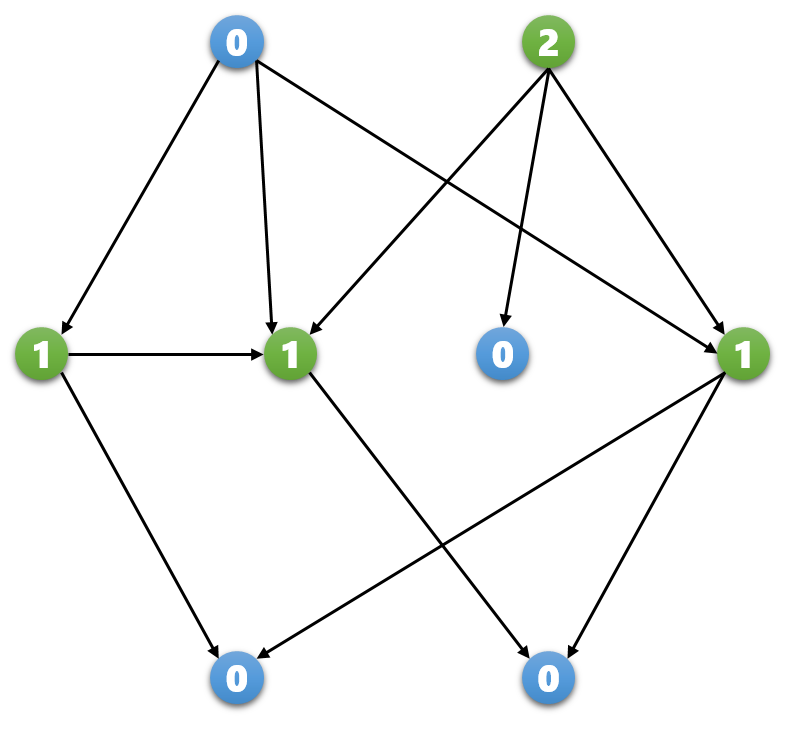
可以发现,若一个局面x为P局面,则有sg(x)=0;否则sg(x)>0。同样sg值也满足N、P之间的转换关系:
若一个局面x,其sg(x)>0,则一定存在一个后续局面y,sg(y)=0。
若一个局面x,其sg(x)=0,则x的所有后续局面y,sg(y)>0。
由上面的推论,我们可以知道用N、P-Position可以描述的游戏用sg同样可以描述。并且在sg函数中还有一个非常好用的定理,叫做sg定理:
对于多个单一游戏,X=x[1..n],每一次我们只能改变其中一个单一游戏的局面。则其总局面的sg值等于这些单一游戏的sg值异或和。
先定义mex(minimal excludant)运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图,定义关于图的每个顶点的Sprague-Grundy函数g如下:g(x)=mex{ g(y) | y是x的后继 },这里的g(x)即sg[x]
例如:取石子问题,有1堆n个的石子,每次只能取{1,3,4}个石子,先取完石子者胜利,那么各个数的SG值为多少?
sg[0]=0,f[]={1,3,4},
x=1时,可以取走1-f{1}个石子,剩余{0}个,mex{sg[0]}={0},故sg[1]=1;
x=2时,可以取走2-f{1}个石子,剩余{1}个,mex{sg[1]}={1},故sg[2]=0;
x=3时,可以取走3-f{1,3}个石子,剩余{2,0}个,mex{sg[2],sg[0]}={0,0},故sg[3]=1;
x=4时,可以取走4-f{1,3,4}个石子,剩余{3,1,0}个,mex{sg[3],sg[1],sg[0]}={1,1,0},故sg[4]=2;
x=5时,可以取走5-f{1,3,4}个石子,剩余{4,2,1}个,mex{sg[4],sg[2],sg[1]}={2,0,1},故sg[5]=3;
以此类推.....
x 0 1 2 3 4 5 6 7 8....
sg[x] 0 1 0 1 2 3 2 0 1....
计算从1-n范围内的SG值。
f(存储可以走的步数,f[0]表示可以有多少种走法)
f[]需要从小到大排序
1.可选步数为1~m的连续整数,直接取模即可,SG(x) = x % (m+1);
2.可选步数为任意步,SG(x) = x;
3.可选步数为一系列不连续的数,用GetSG()计算

//f[]:可以取走的石子个数 //sg[]:0~n的SG函数值 //hash[]:mex{} int f[N],sg[N],hash[N]; void getSG(int n) { int i,j; memset(sg,0,sizeof(sg)); for(i=1;i<=n;i++) { memset(hash,0,sizeof(hash)); for(j=1;f[j]<=i;j++) hash[sg[i-f[j]]]=1; for(j=0;j<=n;j++) //求mes{}中未出现的最小的非负整数 { if(hash[j]==0) { sg[i]=j; break; } } } }

//注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍 //n是集合s的大小 S[i]是定义的特殊取法规则的数组 int s[110],sg[10010],n; int SG_dfs(int x) { int i; if(sg[x]!=-1) return sg[x]; bool vis[110]; memset(vis,0,sizeof(vis)); for(i=0;i<n;i++) { if(x>=s[i]) { SG_dfs(x-s[i]); vis[sg[x-s[i]]]=1; } } int e; for(i=0;;i++) if(!vis[i]) { e=i; break; } return sg[x]=e; }
注意在SG表的初始化中,不用每次都初始;否则会T的,因为可以循环利用,这是一个强大的地方
HDU1536 实战

#include<stdio.h> #include<algorithm> #include<string.h> using namespace std; int s[110],sg[10010],n; char op[200]; int SG_dfs(int x) { int i; if(sg[x]!=-1) return sg[x]; bool vis[110]; memset(vis,0,sizeof(vis)); for(i=0;i<n;i++) { if(x>=s[i]) { SG_dfs(x-s[i]); vis[sg[x-s[i]]]=1; } } int e; for(i=0;;i++) if(!vis[i]) { e=i; break; } return sg[x]=e; } int main() { int k; while(scanf("%d",&n)!=EOF) { if(n==0) break; for(int i=0 ; i<n ; i++) scanf("%d",&s[i]); sort(s,s+n); int m,cnt=0; scanf("%d",&m); memset(sg,-1,sizeof(sg)); for(int i=0 ; i<m ; i++) { scanf("%d",&k); int x=0; while(k--) { int w; scanf("%d",&w); x^=SG_dfs(w); } if(x!=0) printf("W"); else printf("L"); } puts(""); } return 0; }
