对"一维最大子数组和"问题的思考（homework-01）

　　一维最大子数组和问题，即给定一个数组，在它所有的连续子数组的和中，求最大的那个和。“最大子数组和”是一个很好的IT面试考题，在《编程之美》一书中同时阐述了一维数组和二维数组的讨论。本篇博客将会更加细致的讨论一维部分。

　　一. 最直观的 O(n³) 解法

　　在课上看到这个问题，当然最直观的解决办法即穷举。我们通过对子数组的起点和重点进行二层循环，计算每一个子数组的和，取其最大值，这样当然能够解决。但是作为一种O(n³）的解法，显然是低效率的。

　　二. 进一步思考——O(n²)解法

　　为增加程序效率，在接触过的算法中，我们想到或许动态规划能够被运用。动态规划的思想是将前一步的结果存储起来并在后续的步骤中直接使用，减少重复性劳动。因为a[1,10]这样的子数组可以拆解为a[1,9] + a[10], 所以我们可以思考一下如何运用动态规划来增加效率。

　　核心问题是，如何运用动态规划，在哪里用。因为是求和，动态规划就被用来存储已经求和的子数组和，供包含此子数组的子数组的求和来使用。那么，我们仅使用上述O(n³)算法的两层循环，求和过程就简化为线性的复杂度，因此此算法的时间复杂度能被降低为O(n²)。

　　三. 惊艳！——O(n) 解法

　　O(n)算法是我在博客上看到的。看到竟然有O（n）算法，不禁佩服起人类的智慧... 不过，尝试不看解答，我们先想想，是在哪一部分把数量级降低了1呢？要达到O(n)的时间复杂度，必须将循环减至1层。这是容易想到的。问题是：循环减到1层，又如何处理每一层、并且得到最大子数组和呢？下面我们来看看方法：

　　对于一个数组a[1]...a[L-1]，假设我们已经知道其最大子数组和为max_former。当数组增加一个元素a[L]在结尾，那么新数组和最大的子数组要么包含a[L+1]在末尾，要么没有a[L+1]，仍保持原先的子数组不变。用max_updated表示以a[L+1]结尾的最大子数组的和，则增加1个元素后新数组的max_former新=max(max_updated, max_former旧).

　　在max_former旧 已知情况下（动态规划存储的中间步骤）下面只需求max_updated。max_updated旧 表示以a[L-1]结束的最大子数组和。以显然增加一个元素后，max_updated新=max(max_updated旧+a[L+1], a[L+1])。

　　上面两段的思考，我们得到：

　　

max_updated = max(max_updated + a[L], a[L])
max_former = max(max_former, max_updated)

　　四. O(n)代码示例及对比思考

　　　

/*
 * Author: Shone JIN, 11061128
 * Sept. 19, 2013. Version 1.1
 */

#include <fstream>
#include <iostream>
using namespace std;

int max(int a, int b)
{
    return a > b ? a : b;
}

int min(int *a, int l)
{
    int tmp = a[0];
    for (; l > 0; l--){
        if (a[l] < tmp){
            tmp = a[l];
        }
    }
　　　　return tmp;
}
int sum_max(int * a, int l)
{
    int max_former, max_updated;
    max_former = min(a, l);
    max_updated = max_former;

    for (int i = 0; i <= l; i++){
        max_updated = max(max_updated + a[i], a[i]);
        max_former = max(max_former, max_updated);
    }
    return max_former;
}

int main()
{
    int array[100];
    int tmp;
    int i = 0;
    
    ifstream infile("input.txt", ios::in);
    if(! infile){
        cerr << "File Error" << endl;
        exit(1);
    }

    while(! infile.eof()){
        infile >> array[i++];
    }
    
    cout << sum_max(array, i - 1) << endl;
    return 0;
}

　　前面讲到的三个算法，可以理解为循序渐进的优化过程。O(n³)最为直观，当我们尝试使用动态规划存储中间步骤求得的和时，我们将O(n³) 简化为(n²)。至于O(n)算法，就是在动态规划存储上一步结果的前提下，只对子数组末尾元素进行一层循环。这里面运用到了一个巧妙的思维避开了O(n²)算法的两层循环。

　　四. a.程序架构和思路

　　　　max（）返回两个数的最大值，min（）返回一个数组的最小值。整体的程序在从文件中读取数组后，将数组及长度传给函数sum_max()进行求最大子数组和。sum_max（）函数的思想就是前面提到的解法，即对子数组末尾元素循环，找每一个a[0]..a[i]这样的子数组的最大子数组和并求最大值。

　　　　b.心得与体会

　　　　我在课上第一次接触这个问题时陷入了瓶颈，总觉得有很好的解法，但是迟迟无法落笔。经过上面的思考，我领悟到好的算法不总是一下子灵光一闪得到的，而更多的是在不断的改进中得到的。我不需要一次写出最高效的算法，而更应该先把最直观的解法写下，然后一层一层的运用传统的算法进行优化，最终能优化多少，就是多少。

　　　　c.作业中的时间消耗和开发效率分析

　　　　作业的任务量不大，50行，难点在于寻找高效率的解法。在本作业的过程中我使用约1个小时的时间在思考最优秀算法，使用1小时的时间查阅别人的资料并编程，20分钟的测试和修改，30分钟进行Github学习，并签入程序。最后，使用2小时的时间撰写本篇博文。我按时完成了任务，自认为代码质量和很好（代码很短也谈不上...)。总之虽然编程已经有点生疏、慢，但是态度自己还是满意的。

　　　　d.测试结果及程序运行的截图

　　　　首先是数组输入文件，我们举下面的例子：

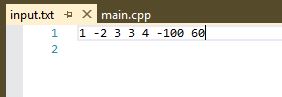
　　　　　其正确解应为60：

　　　　其他的测试数据，可以参考我的Github内容。测试中发现一个问题，无法对全负数数组正确求解，原因是前一个版本的max_former, max_updated初始化为0了，在这里已经修改为是数组的最小元素值。其他并无问题。

　　　　By the way, 受助教老师启发，上面说的max_former, max_updated不用寻找数组最小值也可以得出正确解，而且效率还比较高。我们直接付一个比较小的值就可以，不妨在第一次赋值的时候都赋成a[0]的值，便不对结果产生影响。

　　五. 其他

　　　　我的Github账号： shoneJIN

　　　　我选择的参考书是第二版的《代码大全》