转自:https://yq.aliyun.com/articles/3575
题目
有个长度为2n的数组{a1,a2,a3,…,an,b1,b2,b3,…,bn},希望排序后{a1,b1,a2,b2,….,an,bn},请考虑有无时间复杂度o(n),空间复杂度0(1)的解法。
来源
2013年UC的校招笔试题
思路一
第①步、确定b1的位置,即让b1跟它前面的a2,a3,a4交换:
a1,b1,a2,a3,a4,b2,b3,b4
第②步、接着确定b2的位置,即让b2跟它前面的a3,a4交换:
a1,b1,a2,b2,a3,a4,b3,b4
第③步、b3跟它前面的a4交换位置:
a1,b1,a2,b2,a3,b3,a4,b4
b4已在最后的位置,不需要再交换。如此,经过上述3个步骤后,得到我们最后想要的序列。但此方法的时间复杂度为O(n^2)
代码一
1 /*--------------------------------------------- 2 * 日期:2015-02-13 3 * 作者:SJF0115 4 * 题目: 完美洗牌算法 5 * 来源:2013年UC的校招笔试题 6 * 博客: 7 -----------------------------------------------*/ 8 #include <iostream> 9 using namespace std; 10 11 class Solution { 12 public: 13 void PerfectShuffle(int *A,int n){ 14 if(n <= 1){ 15 return; 16 }//if 17 // 18 int size = 2*n; 19 int index,count; 20 for(int i = n;i < size;++i){ 21 // 交换个数 22 count = n - (i - n) - 1; 23 // 待交换 24 index = i; 25 for(int j = 1;j <= count;++j){ 26 swap(A[index],A[i-j]); 27 index = i - j; 28 }//for 29 }//for 30 } 31 }; 32 33 34 int main() { 35 Solution solution; 36 int A[] = {1,2,3,4,5,6,7,8}; 37 solution.PerfectShuffle(A,4); 38 for(int i = 0;i < 8;++i){ 39 cout<<A[i]<<" "; 40 }//for 41 cout<<endl; 42 }
思路二
我们每次让序列中最中间的元素进行两两交换。还是上面的例子:
a1,a2,a3,a4,b1,b2,b3,b4
第①步:交换最中间的两个元素a4,b1:
a1,a2,a3,b1,a4,b2,b3,b4
第②步:最中间的两对元素各自交换:
a1,a2,b1,a3,b2,a4,b3,b4
第③步:交换最中间的三对元素:
a1,b1,a2,b2,a3,b3,a4,b4
此思路同上述思路一样,时间复杂度依然为O(n^2)。仍然但不到题目要求。
代码二
1 /*--------------------------------------------- 2 * 日期:2015-02-13 3 * 作者:SJF0115 4 * 题目: 完美洗牌算法 5 * 来源:2013年UC的校招笔试题 6 * 博客: 7 -----------------------------------------------*/ 8 #include <iostream> 9 using namespace std; 10 11 class Solution { 12 public: 13 void PerfectShuffle(int *A,int n){ 14 if(n <= 1){ 15 return; 16 }//if 17 // 18 int left = n - 1,right = n; 19 // 交换次数 20 for(int i = 0;i < n-1;++i){ 21 for(int j = left;j < right;j+=2){ 22 swap(A[j],A[j+1]); 23 }//for 24 --left; 25 ++right; 26 }//for 27 } 28 }; 29 30 31 int main() { 32 Solution solution; 33 int A[] = {1,2,3,4,5,6,7,8,9,10}; 34 solution.PerfectShuffle(A,5); 35 for(int i = 0;i < 10;++i){ 36 cout<<A[i]<<" "; 37 }//for 38 cout<<endl; 39 }
思路三(完美洗牌算法)
玩过扑克牌的朋友都知道,在一局完了之后洗牌,洗牌人会习惯性的把整副牌大致分为两半,两手各拿一半对着对着交叉洗牌。
2004年,microsoft的Peiyush Jain在他发表一篇名为:“A Simple In-Place Algorithm for In-Shuffle”的论文中提出了完美洗牌算法。
什么是完美洗牌问题呢?即给定一个数组a1,a2,a3,…an,b1,b2,b3..bn,最终把它置换成b1,a1,b2,a2,…bn,an。这个完美洗牌问题本质上与本题完全一致,只要在完美洗牌问题的基础上对它最后的序列swap两两相邻元素即可。
(1)对原始位置的变化做如下分析:

(2)依次考察每个位置的变化规律:
a1:1 -> 2
a2:2 -> 4
a3:3 -> 6
a4:4 -> 8
b1:5 -> 1
b2:6 -> 3
b3:7 -> 5
b4:8 -> 7
对于原数组位置i的元素,新位置是(2*i)%(2n+1),注意,这里用2n表示原数组的长度。后面依然使用该表述方式。有了该表达式,困难的不是寻找元素在新数组中的位置,而是为该元素“腾位置”。如果使用暂存的办法,空间复杂度必然要达到O(N),因此,需要换个思路。
(3)我们这么思考:a1从位置1移动到位置2,那么,位置2上的元素a2变化到了哪里呢?继续这个线索,我们得到一个“封闭”的环:
1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1
沿着这个环,可以把a1、a2、a4、b4、b3、b1这6个元素依次移动到最终位置;显然,因为每次只移动一个元素,代码实现时,只使用1个临时空间即可完成。(即:a=t;t=b;b=a)
此外,该变化的另外一个环是:
3 -> 6 -> 3
沿着这个环,可以把a3、b2这2个元素依次移动到最终位置。
1 // 走圈算法 2 void CycleLeader(int *a,int start, int n) { 3 int pre = a[start]; 4 // 2 * i % (2 * n + 1) 5 int mod = 2 * n + 1; 6 // 实际位置 7 int next = start * 2 % mod; 8 // 按环移动位置 9 while(next != start){ 10 swap(pre,a[next]); 11 next = 2 * next % mod; 12 }//while 13 a[start] = pre; 14 }
4)上述过程可以通过若干的“环”的方式完整元素的移动,这是巧合吗?事实上,该问题的研究成果已经由Peiyush Jain在10年前公开发表在A Simple In-Place Algorithm for In-Shuffle, Microsoft, 2004中。原始论文直接使用了一个结论,这里不再证明:对于2*n =(3^k-1)这种长度的数组,恰好只有k个环,且每个环的起始位置分别是1,3,9,…3^(k-1)。
对于上面的例子,长度为8,是3^2-1,因此,只有2个环。环的起始位置分别是1和3。
(5)至此,完美洗牌算法的“主体工程”已经完工,只存在一个“小”问题:如果数组长度不是(3^k-1)呢?
若2n!=(3^k-1),则总可以找到最大的整数m,使得m< n,并且2m=(3^k-1)。
对于长度为2m的数组,调用(3)和(4)中的方法整理元素,剩余的2(n-m)长度,递归调用(5)即可。
(6)需要交换一部分数组元素

(下面使用[a,b]表示从a到b的一段子数组,包括端点)
①图中斜线阴影部分的子数组[1,m]应该和[n + 1,n + m]组成一个数组,调用(3)和(4)中的算法;
②数组[m+1,m+n]循环左移n-m次即可。(循环位移是存在空间复杂度为O(1),时间复杂度为O(n)的算法)
(7)原始问题要输出a1,b1,a2,b2……an,bn,而完美洗牌却输出的是b1,a1,b2,a2,……bn,an。解决办法非常简单:忽略原数组中的a1和bn,对于a2,a3,……an,b1,b2,……bn-1调用完美洗牌算法,即为结论。
举个例子: n = 6
a1,a2,a3,a4,a5,a6,b1,b2,b3,b4,b5,b6


循环左移
介绍一下时间复杂度为O(n),空间复杂度为O(1)的循环移位操作。
思路:
假设循环左移m位。把数组分成两段,第一段为前m个元素,第二段为剩余元素。把第一段和第二段先各自翻转一下,再将整体翻转下。
1 // 翻转 start 开始位置 end 结束位置 2 void Reverse(int *a,int start,int end){ 3 while(start < end){ 4 swap(a[start],a[end]); 5 ++start; 6 --end; 7 }//while 8 } 9 // 循环左移m位 n数组长度 下标从1开始 10 void LeftRotate(int *a,int m,int n){ 11 // 翻转前m位 12 Reverse(a,1,m); 13 // 翻转剩余元素 14 Reverse(a,m+1,n); 15 // 整体翻转 16 Reverse(a,1,n); 17 }
代码:
1 /*--------------------------------------------- 2 * 日期:2015-02-13 3 * 作者:SJF0115 4 * 题目: 完美洗牌算法 5 * 来源:2013年UC的校招笔试题 6 * 博客: 7 -----------------------------------------------*/ 8 #include <iostream> 9 using namespace std; 10 11 class Solution { 12 public: 13 // 完美洗牌算法 14 void PerfectShuffle(int *a,int n){ 15 while(n >= 1){ 16 // 计算环的个数 17 int k = 0; 18 // 3^1 19 int r = 3; 20 // 2 * m = 3^k - 1 21 // m <= n -> 2 * m <= 2 * n -> 3^k - 1 <= 2 * n 22 // 寻找最大的k使得3^k - 1 <= 2*n 23 while(r - 1 <= 2*n){ 24 r *= 3; 25 ++k; 26 }//while 27 int m = (r / 3 - 1) / 2; 28 // 循环左移n-m位 29 LeftRotate(a+m,n-m,n); 30 // k个环 环起始位置start: 1,3...3^(k-1) 31 for(int i = 0,start = 1;i < k;++i,start *= 3) { 32 // 走圈 33 CycleLeader(a,start,m); 34 }//for 35 a += 2*m; 36 n -= m; 37 } 38 } 39 private: 40 // 翻转 start 开始位置 end 结束位置 41 void Reverse(int *a,int start,int end){ 42 while(start < end){ 43 swap(a[start],a[end]); 44 ++start; 45 --end; 46 }//while 47 } 48 // 循环右移m位 n数组长度 下标从1开始 49 void LeftRotate(int *a,int m,int n){ 50 // 翻转前m位 51 Reverse(a,1,m); 52 // 翻转剩余元素 53 Reverse(a,m+1,n); 54 // 整体翻转 55 Reverse(a,1,n); 56 } 57 // 走圈算法 58 void CycleLeader(int *a,int start, int n) { 59 int pre = a[start]; 60 // 2 * i % (2 * n + 1) 61 int mod = 2 * n + 1; 62 // 实际位置 63 int next = start * 2 % mod; 64 // 按环移动位置 65 while(next != start){ 66 swap(pre,a[next]); 67 next = 2 * next % mod; 68 }//while 69 a[start] = pre; 70 } 71 }; 72 73 74 int main() { 75 Solution solution; 76 int A[] = {0,1,2,3,4,5,6,7,8,9,10,11,12}; 77 solution.PerfectShuffle(A,6); 78 for(int i = 1;i <= 12;++i){ 79 cout<<A[i]<<" "; 80 }//for 81 cout<<endl; 82 }
拓展一
问题:如果输入是a1,a2,……an, b1,b2,……bn, c1,c2,……cn,要求输出是c1,b1,a1,c2,b2,a2,……cn,bn,an怎么办?
分析: 这个问题本质上其实还是上面的完美洗牌算法一样,我们一样还是分析其规律。
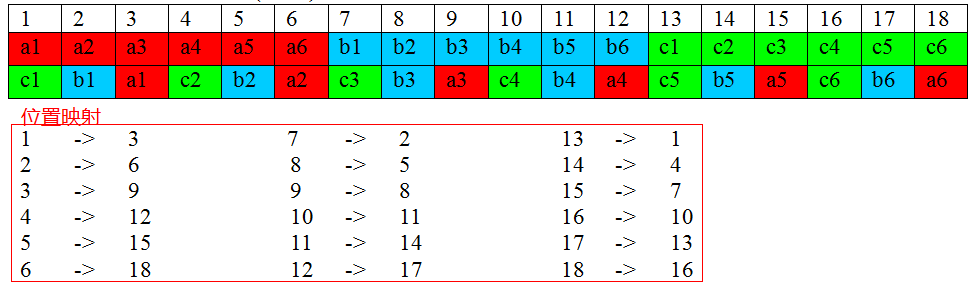
对于原数组位置i的元素,新位置是(3*i)%(3n+1)
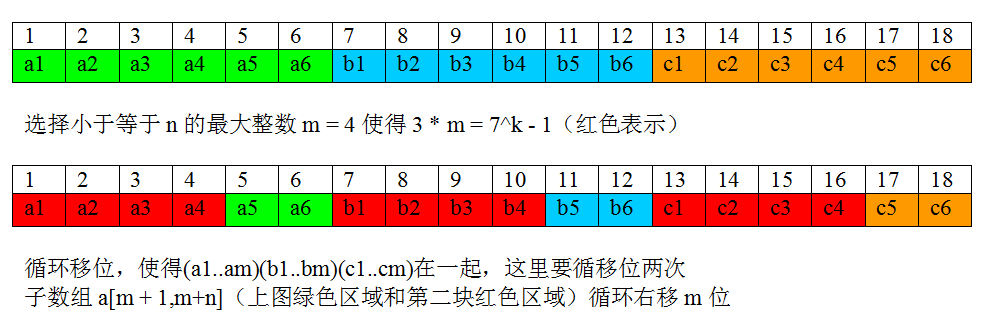

图中所说的步骤三四五和上面的三四五大体一样,只是细节不太一样,看图就明白了。
引用:
http://blog.csdn.net/v_july_v/article/details/10212493
http://ask.julyedu.com/question/33
http://blog.csdn.net/caopengcs/article/details/10521603
http://cs.stackexchange.com/questions/332/in-place-algorithm-for-interleaving-an-array/400#400