
2017年,“比特币”一定是最让人疯狂的名词之一。比特币的价格,从年初的不到1000美元的,一路高歌猛进到最高的5000多美元,并被越来越多市场和机构采纳。
让人瞠目结舌的上涨速度,也带动了越来越多的人投身“挖矿”的热潮之中。摩尔定律甚至也因此失去了作用——显卡等计算机设备不但没有降价,还一路上涨。比特币背后的区块链技术,更被称为下一个可能改变世界的技术。
看到这里你一定很好奇,比特币是什么,接下来将带您领略比特币的魅力~
|实验楼推出《比特币基础概念入门》,从比特币的密码学原理、交易原理等层面,将一步步地为你揭开区块链技术的面纱……
课程介绍
本课程从比特币的密码学原理,交易原理等等方面展开,一层一层地揭开区块链技术的面纱,带领同学们领略来自未来的技术。
-
实验列表:

-
实验环境
·Python
二、加密算法和数字签名
1 .实验知识点
·比特币简介
·加密算法
·交易与数字签名
-
比特币简介
比特币是什么呢? 确切地说,比特币有多种含义,很多人在谈论比特币时存在概念上的混淆,下面我们分别阐述比特币的不同含义:
从技术层面来看,比特币是最早和最成功的区块链应用,它可以被看作一个由加密算法,共识机制,p2p网络等技术组合而成的系统。由于这个系统在不停地分发货币,所以它也可以被看成是一个世界银行,但是与普通银行不同的是,它的运行者不是特定的中心权威而是网络上的节点。另外这个系统分发的货币也被称作比特币,如果要避免混淆我们也可以用BTC来指代这种货币。
比特币的价值在于,比特币与其他虚拟货币不同,它的其总数量非常有限,具有极强的稀缺性。 -
加密算法
比特币是什么呢? 确切地说,比特币有多种含义,很多人在谈论比特币时存在概念上的混淆,下面我们分别阐述比特币的不同含义:
3.1 私钥、公钥与比特币地址
在现代社会中,一种大量流通的货币一般都有非常高级的加密技术,例如人民币上就有水印、荧光光圈等一系列技术来提高伪造的难度。数字货币在本质上是网络上的数据,非常容易受到攻击,所以需要一套完善的加密体系。
就像我们在银行有账户密码一样,在比特币中我们也有一些相似的东西来决定一个账户的所有权。具体来说有三个与账户相关的概念:私钥、公钥和比特币地址。
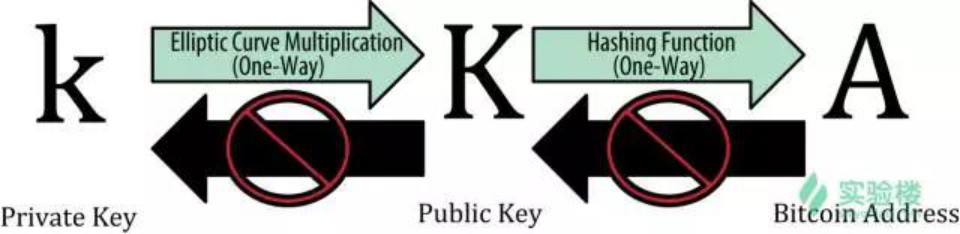
他们之间的关系如上图所示,私钥可以通过椭圆加密算法生成公钥,公钥可以通过哈希函数生成比特币地址。反过来看,有了比特币地址是无法生成公钥的,有了公钥也无法生成私钥,这是由后面要介绍的加密算法所实现的。
值得一提的是,掌握私钥就能生成相应的公钥和比特币地址,相当于掌握了整个账户,所以我们一定要保管好自己的私钥。
下面我们简单介绍一下椭圆加密算法和哈希函数:
3.2 椭圆加密算法
从私钥到公钥所用的是椭圆加密算法,它有一个简单的数学形式,即
K = k * G
其中K代表公钥,k代表私钥,而G代表椭圆曲线上面的一点,这个乘法不是自然数的乘法,而是椭圆乘法 。 关于椭圆曲线及其乘法比较完整的数学定义可以参考Mathworld: Elliptic Curve 和椭圆曲线密码学简介。
下面是这个算法的一些要点:
1 . 椭圆曲线的一般形式:
y2 = x3 + ax +b
所构成的点的集合
2.椭圆曲线的加法的计算方法 (x1,y1) + (x2,y2) = (x3,y3)

3.通过计算 G+G 算出 2G , 继而算出 4G,最终通过大约 log2(k) 次算出 k * G , 由于每次的计算量不大,所以总体计算量也不大。
4.要根据 K 和 G 得到 k 的问题叫做离散对数问题 ,计算复杂度为根号 p, 其中 p 为整个群的大小,(如果 n 位二进制那么复杂度就是 2n/2)这个复杂度是非常可怕的,几乎没有可能求解出来,换句话说,根据公钥反向计算私钥基本上是不可能的。
3.3 哈希函数
从公钥生成比特币地址的过程所用的是哈希函数,它在比特币系统的多个地方都有应用。
哈希函数有很多种,一般有如下定义:
输入是任意长度的字符串
输出是固定长度的数字(例如比特币一般用 256 位)
计算非常简单
从安全角度来看,它有下面的特征:
没有碰撞:对于 x 和 y , 如果 x 不等于 y , 那么我们可以保证 H(x) 不等于 H(y)。这条性质是概率上的保证,因为我们的输入集合是一个无限的集合,而输出是一个只有2的256次方的集合,根据抽屉原理必然存在x1与x2不相等但是H(x1)等于H(x2)的情况 ,但是Hash函数的设计会让这个概率非常非常小,小到几乎不可能发生。
隐藏性质:从x可以生成H(x) , 但是几乎无法从H(x)生成x , 这条性质保证我们无法由比特币地址得到公钥。
3.4 代码
下面是生成私钥、公钥、比特币地址的一段示例代码 。 椭圆加密算法使用的是 python 的 ecdsa 库,哈希算法使用的是 hashlib 。 另外没讲到的部分是 base58Checkencode , 这是在表示比特币地址时所用的方法,可以把地址压缩得更短 ,使得表示更为清晰。
读者可以看一看这段代码,实际操作一下来理解比特币的加密原理。
import ecdsa
import ecdsa.der
import ecdsa.util
import hashlib
import os
import re
import struct
b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz' def base58encode(n):
result = '' while n > 0:
result = b58[n%58] + result
n /= 58 return result
def base256decode(s):
result = 0 for c in s:
result = result * 256 + ord(c)
return result
def countLeadingChars(s, ch):
count = 0 for c in s:
if c == ch:
count += 1 else:
break return count
https://en.bitcoin.it/wiki/Base58Check_encoding def base58CheckEncode(version, payload):
s = chr(version) + payload
checksum = hashlib.sha256(hashlib.sha256(s).digest()).digest()[0:4]
result = s + checksum
leadingZeros = countLeadingChars(result, '�')
return '1' * leadingZeros + base58encode(base256decode(result))
def privateKeyToWif(key_hex): return base58CheckEncode(0x80, key_hex.decode('hex'))
def privateKeyToPublicKey(s):
sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1)
vk = sk.verifying_key
return ('�4' + sk.verifying_key.to_string()).encode('hex')
def pubKeyToAddr(s):
ripemd160 = hashlib.new('ripemd160')
ripemd160.update(hashlib.sha256(s.decode('hex')).digest())
return base58CheckEncode(0, ripemd160.digest())
def keyToAddr(s): return pubKeyToAddr(privateKeyToPublicKey(s))
Generate a random private key
private_key = os.urandom(32).encode('hex')
You can verify the values on http://brainwallet.org/ print "Secret Exponent (Uncompressed) : %s " % private_key
print "Public Key : %s" % privateKeyToPublicKey(private_key)
print "Private Key : %s " % privateKeyToWif(private_key)
print "Address : %s " % keyToAddr(private_key)
打开实验楼在线环境,首先需要通过终端安装 ecdsa 包:
sudo pip install ecdsa
安装完成之后,推荐通过在线环境桌面上就能看到的 gedit 编辑器书写代码。最终保存并运行结果如下:

四、交易与数字签名
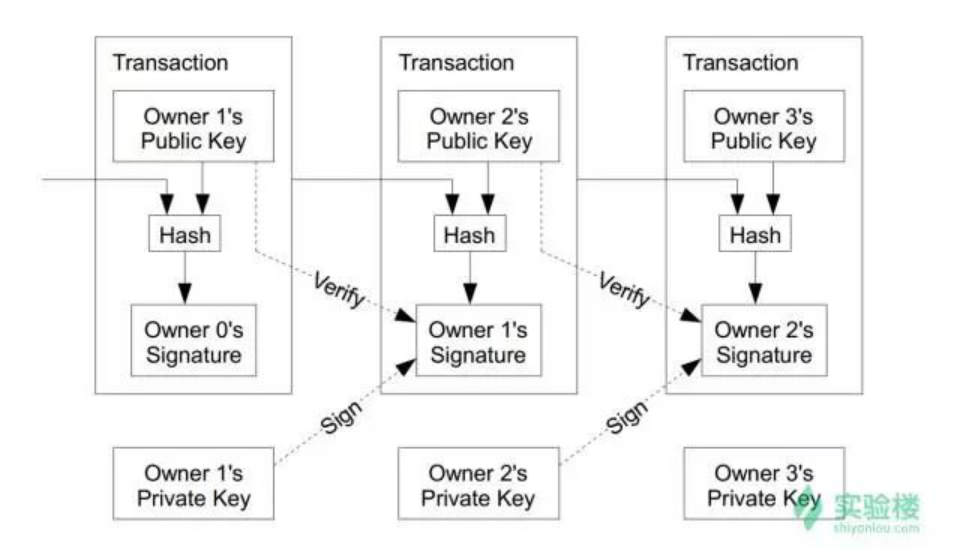
在了解到私钥和公钥的概念后,我们来看一看比特币内部的交易是怎么做的。 从上面这幅图可以看到,一个方框代表一笔交易,例如中间的方块代表的是由 owner1 支付给 owner2 的一次交易,我们可以看到在方框下方有一个签名,正是这个签名让这次交易有效。
这个签名签署用到的是 owner1的私钥 和与这次交易的相关信息(包括前一次交易,owner2公钥,金额,时间戳等信息),用 api 的形式进行表达就是:
sig := sign(sk, message)
其中sig代表签名,sign是签名函数,sk代表私钥,message代表交易相关信息
而签名完成后,其他人要有办法验证这笔交易是否有效,所以它们要用 owner1的公钥,交易相关信息以及签名完成验证,用 api 的形式来表达就是
isValid := verify(pk, message, sig)
这里的pk代表公钥,isValid是一个布尔变量,其值为真或假。
从上面的两个 api 我们可以看到数字签名有一系列好的性质,一个性质是我们在签名的时候用到私钥,但是验证时只用公钥,这保证了私钥的安全性。第二个是签名与每次交易对应,我们不能把签名迁移到另一次交易上,只要私钥不泄露别人就无法伪造签名。
五、总结
在本节中我们介绍了私钥、公钥和比特币地址以及它们之间转换时所使用的加密算法。另外我们还对比特币系统内的交易原理进行了介绍,这些内容是比特币系统中非常基础的内容。
在下一节中,我们会对存储这些交易记录的数据结构进行介绍,也就是传说中的“区块链” 。
做到这里,课程只进行了3分之1,后续步骤及详细代码请点击《比特币基础概念入门》观看。学编程,动手敲代码是最有用的方式,请大家到实验楼动手学习这个项目。
更多经典的编程练手项目:全部课程
微信关注公众号[实验楼],手机查看海量项目教程。