用二进制来表示一个问题的子问题是否使用过,例如,101表示1、3已经使用,2没有使用过。由于使用指数级别的数据所以一般使用状压DP的数据范围不会很大,不超过30,一般使用在解决NP问题的小规模求解中。
一些操作:
x>>n x<<n
x&y x|y x^y(异或)
1<<i 左移i位
x|(1<<i-1) 把x的第i位变为1 ,if(x&(1<<i-1)) 判断x的第i位是不是1
x=x&(x-1) 把x的最后一个1去掉
for(int i=x;i;i=(i-1)&x) 枚举x的子集
x&(-x) 返回x最后一个1的位置
1、[SCOI2009]围豆豆
题目背景
四川NOI2009省选
题目描述
是不是平时在手机里玩吃豆豆游戏玩腻了呢?最近MOKIA手机上推出了一种新的围豆豆游戏,大家一起来试一试吧。
游戏的规则非常简单,在一个N×M的矩阵方格内分布着D颗豆子,每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格,每次移动可以随意的走到相邻的四个格子,直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物,任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0,即什么都不做。
注意路径包围的概念,即某一颗豆在路径所形成的多边形(可能是含自交的复杂多边形)的内部。下面有两个例子:
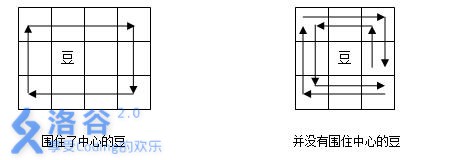
第一个例子中,豆在路径围成的矩形内部,所以豆被围住了。第二个例子中,虽然路径经过了豆的周围的8个格子,但是路径形成的多边形内部并不包含豆,所以没有围住豆子。
布布最近迷上了这款游戏,但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。
输入格式
第一行两个整数N和M,为矩阵的边长。
第二行一个整数D,为豆子的总个数。
第三行包含D个整数V1到VD,分别为每颗豆子的分值。
接着N行有一个N×M的字符矩阵来描述游戏矩阵状态,0表示空格,#表示障碍物。而数字1到9分别表示对应编号的豆子。
输出格式
仅包含一个整数,为最高可能获得的分值。
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3fffffff;
//状态压缩+SPFA
//!!!!!射线法:判断点是不是在多边形内
//题目:https://www.luogu.com.cn/problem/P2566
//题解:https://blog.csdn.net/zhouyuyang233/article/details/70215607
int dis[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
struct point{
int x,y;
}b[15];
struct node{
int i,j,s; //i,j是坐标,s是状态
};
queue<node> q;
char mp[12][12]; //地图
int dp[12][12][520]; //分别是坐标、状态、代表的是需要走的最少步数
int w[12]; //豆子的价值
int n,m,d,ans;
int cross(int x,int y,int nx,int ny,int s){
for(int i=1;i<=d;i++){ //枚举每一个豆子
if(((x<b[i].x&&nx>=b[i].x)||(x>=b[i].x&&nx<b[i].x))&&y>b[i].y) //得到奇数个交点,被包围了
s^=1<<(i-1); //更新包围的豆子状态
}
return s;
}
void spfa(int sx,int sy){
q.push((node){sx,sy,0});
memset(dp,0x3f,sizeof(dp)); //把dp赋值为一个很大的数,因为要求最小
dp[sx][sy][0]=0;
while(!q.empty()){
node x=q.front();
q.pop();
for(int i=0;i<4;i++){
int xx=x.i+dis[i][0];
int yy=x.j+dis[i][1];
if(xx<1||xx>n||yy<1||yy>m||mp[xx][yy]!='0') continue;
int s=cross(x.i,x.j,xx,yy,x.s); //这次转移的两次坐标
if(dp[xx][yy][s]>dp[x.i][x.j][x.s]+1){
dp[xx][yy][s]=dp[x.i][x.j][x.s]+1; //减小步数
//更新后的
q.push((node){xx,yy,s});
}
}
}
for(int i=0;i<1<<d;i++){
int res=-dp[sx][sy][i]; //每个状态需要走过的步数
for(int j=1;j<=d;j++){ //然后枚举每个步数
if(i&(1<<(j-1))) res+=w[j]; //这个被包括了
}
ans=max(ans,res);
}
}
int main(){
scanf("%d %d %d",&n,&m,&d);
for(int i=1;i<=d;i++) scanf("%d",&w[i]);
//string s;
for(int i=1;i<=n;i++){
scanf("%s",mp[i]+1);
for(int j=1;j<=m;j++){
if(mp[i][j]>='1'&&mp[i][j]<='9') {
int x=mp[i][j]-'0';
point xx;
xx.x=i;xx.y=j;
b[x]=xx;
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(mp[i][j]=='0') spfa(i,j); //对每一个空格进行枚举
}
}
printf("%d
",ans);
return 0;
}
2、最短Hamilton路径,每个点只经过一次
伪代码:
//dp[k][i|1<<(k-1)]=min(dp[k][i|1<<(k-1)],dp[j][i]+a[j][k]) //从j到k
memset(dp,0x3f,sizeof(dp));
dp[1][1]=0;
for(int i=1;i<(1<<n);i++){
for(int j=1;j<=n;j++){
if(i&(1<<j-1)){ //第j位为1,已经去过了
for(int k=1;k<=n;k++){
if(!(i&(1<<k-1))){ //第k位没去过
dp[k][i|1<<(k-1)]=min(dp[k][i|1<<(k-1)],dp[j][i]+a[j][k]);
}
}
}
}
}
cout<<dp[n][(1<<n)-1];
3、哈密尔顿回路(插头动态规划)
讲解
https://www.luogu.com.cn/problemnew/solution/P5056
https://blog.csdn.net/litble/article/details/79369147
4、玉米田
农场主John新买了一块长方形的新牧场,这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12),每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是John不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int mod = 100000000;
int n, m;
int a[13][13];
int F[13];
//第[i]行的土地状态
int f[13][1 << 12 + 5];
//f[i][j]前[i]行的状态为j时的合法方案数 注意是前i行不是第i行
bool g[1 << 12 + 5];
int main() {
scanf("%d %d", &m, &n);
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &a[i][j]);
F[i] = (F[i] << 1) + a[i][j];
}
}
for (int i = 0; i < (1 << n); i++)
g[i] = (!(i & (i << 1))) && (!(i & (i >> 1)));
f[0][0] = 1;
for (int i = 1; i <= m; i++) {
//枚举每行
for (int j = 0; j < (1 << n); j++) {
//枚举这行每个可能的状态
if (g[j] && ((j & F[i]) == j)) {
for (int k = 0; k < (1 << n); k++) {
//枚举上一行的状态
if ((k & j) == 0) {
//与该行状态取&为0说明上一行与这一行不存在任意一块草地有公共边
f[i][j] = (f[i][j] + f[i - 1][k]) % mod;
}
}
}
}
}
int ans = 0;
for (int i = 0; i < (1 << n); i++) {
ans = (ans + f[m][i]) % mod;
//最后将前m行所有满足条件的方案数累加
}
printf("%d
", ans);
return 0;
}
5、关灯问题
现有n盏灯,以及m个按钮。每个按钮可以同时控制这n盏灯——按下了第i个按钮,对于所有的灯都有一个效果。按下i按钮对于第j盏灯,是下面3中效果之一:如果a[i][j]为1,那么当这盏灯开了的时候,把它关上,否则不管;如果为-1的话,如果这盏灯是关的,那么把它打开,否则也不管;如果是0,无论这灯是否开,都不管。
现在这些灯都是开的,给出所有开关对所有灯的控制效果,求问最少要按几下按钮才能全部关掉。
int a[110][1010]; //记录按钮对应的灯情况
bool vis[1000010];// 判断这个状态有没有经历过
struct node{
int sta;
int step;
}; //这个时记录状态的,到达这个状态需要的次数
int n,m;
//由于初始状态是1<<n-1,结尾是0,所以可以从1<<n-1为起点,以0为终点,开始BFS,记录最短步数
//也就是SPFA算法
queue<node> q;
int spfa(){
q.push((node){(1<<n)-1,0}); //入队
vis[(1<<n)-1]=1;
while(!q.empty()){
node temp=q.front();
q.pop();
int ss=temp.sta;
if(ss==0){
return temp.step; //如果到了就返回
}
for(int i=1;i<=m;i++){
ss=temp.sta;
for(int j=1;j<=n;j++){
if(a[i][j]==1&&(ss&(1<<j-1))) ss^=(1<<j-1); //异或,如果本身是1开着的,那么就会关掉
else if(a[i][j]==-1&&!(ss&(1<<j-1))) ss|=(1<<j-1); //如果本身是关着的,那么就会开上
}
if(!vis[ss]){
q.push((node){ss,temp.step+1});
vis[ss]=1;
}
}
}
return -1;
}
int main(){
scanf("%d %d",&n,&m); //灯、按钮
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);
printf("%d
",spfa());
return 0;
}
6、铺砖块
给定一个N*M(N<=5,M<=1000)的棋盘,可以用2*1,1*2的砖块取填充,问有多少中方案
dp[i][state]表示填充第i列,第i-1列带给他的影响是state时的方案数,N小,所以可以搜索全部可能的放置方式,记录对下一列的影响,之后更新状态
int N, M;
long long dp[1005][34];
void dfs(int i,int j,int state,int nex)
{
if (j==N)
{
dp[i+1][nex]+=dp[i][state];
return;
}
//如果这个位置已经被上一列所占用,直接跳过
if (((1<<j)&state)>0)
dfs(i,j+1,state,nex);
//如果这个位置是空的,尝试放一个1*2的
if (((1<<j)&state)==0)
dfs(i,j+1,state,nex|(1<<j));
//如果这个位置以及下一个位置都是空的,尝试放一个2*1的
if (j+1<N && ((1<<j)&state)==0 && ((1<<(j+1))&state)==0)
dfs(i,j+2,state,nex);
return;
}
int main()
{
while (cin>>N>>M)
{
memset(dp,0,sizeof(dp));
if (N==0 && M==0) break;
dp[1][0]=1;
for (int i=1;i<=M;i++)
{
for (int j=0;j<(1<<N);j++)
if (dp[i][j])
{
dfs(i,0,j,0);
}
}
cout<<dp[M+1][0]<<endl;
}
}
一本通的题
1592:【例 1】国王
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入:n,k
f[i][j][k]代表的是前i行并且第i行的状态是j&&安排的骑士个数是k时的合法方案
j原本是一维的有n个元素的数组,代表的是第i行的状态,但是对于状态只有01两种选择,放与不放
所以可以将01串看作二进制数,则每一个状态对应一个唯一的十进制数,这就是这一题的核心思想状压
f[i][now][tot]+=f[i-1][pre][tot-num[now]]; //重点
for(int i=1;i<=ans;i++){
op+=f[n][i][k];
}
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int summ=1024; //2^10
const int INF=0x3fffffff;
typedef long long LL;
int n,k;
LL ans,cnt;
LL f[11][150][maxn];
//f[i][j][k]代表的是前i行并且第i行的状态是j&&安排的骑士个数是k时的合法方案
//j原本是一维的有n个元素的数组,代表的是第i行的状态,但是对于状态只有01两种选择,放与不放
//所以可以将01串看作二进制数,则每一个状态对应一个唯一的十进制数,这就是这一题的核心思想状压
LL s[maxn],num[maxn];
//s存储的是合理方案,num是这个方案有的国王数量
void pre(){
for(LL i=0;i<(1<<n);i++){
if(i&(i<<1)) continue; //两个1连在一起
cnt=0;
for(int j=0;j<n;j++){
if(i&(1<<j)) cnt++;
}
s[++ans]=i; //方案
num[ans]=cnt; //国王数量
}
}
LL op=0;
void solve(){
f[0][1][0]=1; //代表的是第0行不放时有1种选择,为什么第二个下标是1呢,因为s[1]为一个长度为n的只包含0的字符串
for(int i=1;i<=n;i++){
for(LL now=1;now<=ans;now++){
for(LL pre=1;pre<=ans;pre++){
if(!(s[now]&s[pre])){//如果上下两行之间没有列号为x的都是1的情况,继续
for(int tot=num[now];tot<=k;tot++){ //个数
if((!(s[now]&(s[pre]<<1)))&&(!(s[now]&(s[pre]>>1)))){//判断对角线是否满足要求
f[i][now][tot]+=f[i-1][pre][tot-num[now]];
}
}
}
}
}
}
for(int i=1;i<=ans;i++){
op+=f[n][i][k];
}
printf("%lld
",op);
}
int main(){
scanf("%d %d",&n,&k);
pre();
solve();
return 0;
}
1593:【例 2】牧场的安排
和前面的玉米田是同一道题
同样,理解这个状态转移,上面和这道题都有一个矩阵的形式,所以可以考虑上下行之间的约束关系,由上一行的合法状态转移到现在这一行的合法状态
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int MOD=1e8;
const int INF=0x3fffffff;
typedef long long LL;
int dp[13][1<<12+10];
bool vis[1<<12+10];
int n,m;
int a[13][13]; //土地状态
int f[13]; //第i行的土地状态
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
f[i]=(f[i]<<1)+a[i][j];
}
}
for(int i=0;i<(1<<m);i++){
vis[i]= (!(i & (i << 1))) && (!(i & (i >> 1)));
}
dp[0][0]=1;
for(int i=1;i<=n;i++){
//每一行
for(int j=0;j<(1<<m);j++){ //这一行的每个可能状态
if(vis[j]&&(j&f[i]==j)){ //真正理解这个j&f[i]==j的含义
for(int k=0;k<(1<<m);k++){ //上一行状态为k
if((j&k)==0){
dp[i][j]=(dp[i][j]+dp[i-1][k])%MOD;
}
}
}
}
}
int ans=0;
for(int i=0;i<(1<<m);i++){
ans=(ans+dp[n][i])%MOD; //可能的所有状态
}
printf("%d
",ans);
return 0;
}
1594:涂抹果酱

看到了没有,三种果酱,所以是三进制DP,同时注意已经涂了KK行,所以KK行具体是第几行有影响的
有两个函数check(int x) 用来x状态可不可以
函数judge(int x,int y) 用来判断上下两行相邻区域有没有使用相同的果酱,都是利用三进制的特点
同样也是利用上下两行的状态转移(合法)来累计
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=10100;
const int MOD=1e6;
const int INF=0x3fffffff;
typedef long long LL;
//因为有三种果酱,三种状态,所有要用三进制
LL n,m,k,ans,tot,stat;
LL sta[1010];
LL f[maxn][1010];
bool check(LL x){ //检查x状态可不可以
int temp=63;
for(int i=1;i<=m;i++){
if(temp==x%3) return false; //检查左右移
temp=x%3;//这一位与下一位相同
x/=3;//%3表示取那一位的状态 x/3表示下一位
}
return true;
}
bool judge(LL a,LL b){
for(int i=1;i<=m;i++){
if(a%3==b%3) return false;
a/=3;
b/=3;
}
return true;
}
int main(){
cin>>n>>m>>k;
stat=1;
for(int i=1;i<=m;i++) stat*=3; //三进制不能用 1<<i ,每一位是3个组合态,所以是3^i次方
for(LL i=0;i<stat;i++){ //0-stat之间的每一个i表示一个3进制m位的组合态
if(check(i)) sta[++ans]=i; //符合要求的可能组合状态
}
LL ban=0; //已经确定了的那一行的状态
for(int i=1;i<=m;i++){
int t;
cin>>t;
ban=ban*3+t-1; //秦九韶公式???
}
int pos=0;
for(LL i=1;i<=ans;i++){
if(sta[i]==ban){
pos=i;break;
}
}
//cout<<ans<<" "<<ban<<" "<<pos<<endl;
if(pos==0){ //本身就不是合法的状态
cout<<"0";return 0;
}
//下面就是状态转移了,根据上一行和下一行的关系递推
for(int i=1;i<=n;i++){
if(i==k){ //遇到了确定的那一行
if(i==1) f[i][pos]=1; //如果是第一行
else{
for(LL k=1;k<=ans;k++){ //上一行状态
if(judge(sta[pos],sta[k]))
//(f[i][pos]+=f[i-1][k])%=MOD;
f[i][pos]=(f[i][pos]+f[i-1][k]%MOD)%MOD;
}
}
}
else
for(LL j=1;j<=ans;j++){ //这一行的状态 因为没有涂过,所以全部的状态(合法)都可以
if(i==1) f[i][j]=1; //第一行
else
for(LL k=1;k<=ans;k++) //上一行
if(judge(sta[j],sta[k]))
// (f[i][j]+=f[i-1][k])%MOD;
f[i][j]=(f[i][j]+f[i-1][k]%MOD)%MOD;
}
}
for(LL i=1;i<=ans;i++){
(tot+=f[n][i])%MOD;
}
cout<<tot;
return 0;
}
//。。。。。。。。。。明明一样的。。。我的超时
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
#define ll long long
#define mod 1000000
#define N 10005
using namespace std;
int n,m,K,ban,ans=0,sta[1005],tot=0,stat,f[N][1005],bit[6],pos;
bool check(int x){
int tmp=63;
for(int i=1;i<=m;++i){//检查左右移
if(tmp == (x % 3)) return false;//这一位与下一位相同
tmp =x % 3,x/=3; //%3表示取那一位的状态 x/3表示下一位
}
return true;
}
bool judge(int a,int b){ //用来判断上下两行是否合法
for(int i=1;i<=m;++i){
if(a % 3 == b % 3)return false;
a/=3,b/=3;
}
return true;
}
int main(){
cin>>n>>m>>K;//n行,m列,第K行已经涂色
stat=1;
for(int i=1;i<=m;++i) stat*=3; //三进制不能用 1<<i ,每一位是3个组合态,所以是3^i次方
for(int i=0;i < stat;++i) //0-stat之间的每一个i表示一个3进制m位的组合态
if(check(i)) sta[++tot]=i; //符合要求的可能组合状态
for(int i=1;i<=m;++i){
int t;cin>>t;//输入已经确定的第k行的状态
ban=ban*3 + t -1;//秦九韶公式
}
for(int i=1;i<=tot;++i) if(ban==sta[i]){pos=i;break;} //看看是否存在一种可能状态,与之吻合
if(!pos){puts("0");return 0;} //这种状态的本身,就不符合要求
for(int i=1;i<=n;++i)
{
if(i==K){
if(i==1) f[i][pos]=1;
else
for(int j=1;j<=tot;++j)
if(judge(sta[pos],sta[j])) (f[i][pos]+=f[i-1][j])%=mod;
}else
for(int j=1;j<=tot;++j)
{
if(i==1) f[i][j]=1;
else
for(int k=1;k<=tot;++k)
if(judge(sta[j],sta[k])) (f[i][j]+=f[i-1][k])%=mod;
}
}
for(int i=1;i<=tot;++i) (ans+=f[n][i])%=mod;
cout<<ans;
return 0;
}
另一道三进制DP hdu 3001 travelling
另一种简化的TSP,n<=10,可以从每个城市出发,每个城市不经过两次以上,求最少的路径和
int tri[60000][11]; //表示第i个路径,第j位的状态为
int dp[11][60000]; //当前所在城市位i,dp[i][j]表示从i出发访问剩余的所有城市之后回到起点的路径费用的综合最小值
还是不是很懂
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=1010;
const int INF=0x3f3f3f3f;
typedef long long LL;
//又是一道三进制压缩dp
int n,m;
int bit[12]={0,1,3,9,27,81,243,729,2187,6561,19683,59049};
int tri[60000][11]; //表示第i个路径,第j位的状态为
int dp[11][60000]; //当前所在城市位i,dp[i][j]表示从i出发访问剩余的所有城市之后回到起点的路径费用的综合最小值
int graph[11][11];
//dp[j][i]=min(dp[j][i],dp[k][l]+graph[k][j])
void make_trb(){ //初始化
for(int i=0;i<59050;i++){
int t=i;
for(int j=1;j<=10;j++) {
tri[i][j]=t%3;t/=3;
}
}
}
int dpp(){
int ans=INF;
memset(dp,INF,sizeof(dp));
for(int i=0;i<=n;i++) dp[i][bit[i]]=0; //从bit[i]是第i个城市,起点任意
for(int i=0;i<bit[n+1];i++){
int flag=1;
for(int j=1;j<=n;j++){
if(tri[i][j]==0){
flag=0;
continue;
}
if(i==j) continue;
//去过j
for(int k=1;k<=n;k++){
int l=i-bit[j]; //第j位置0
if(tri[i][k]==0) continue; //第k位没去过,但是需要第k位去过
dp[j][i]=min(dp[j][i],dp[k][l]+graph[k][j]);
}
}
if(flag){
for(int j=1;j<=n;j++) ans=min(ans,dp[j][i]);
}
}
return ans;
}
int main(){
make_trb();
while(cin>>n>>m){
memset(graph,INF,sizeof(graph));
while(m--){
int a,b,c;
cin>>a>>b>>c;
if(c<graph[a][b]) graph[a][b]=graph[b][a]=c;
}
int ans=dpp();
if(ans==INF) cout<<"-1"<<endl;
else cout<<ans<<endl;
}
return 0;
}
1595:炮兵阵地

受影响的范围扩大了
DP[raw][i][j] : 在第 raw 行状态为 i, 第 raw - 1 行状态为 j 的情况
注意:观察到这道题和例一国王一样其实求得都是最多摆放个数,所以都求了两个数组,分别是sta[],num[],用来存储合法情况,这种合法情况含有的数量
所以最后都需要利用这两个数组
由于这道题的影响范围扩大,所以在最后循环的时候,有四重,第一重就是 i=1~n为层数
第二重是 j=0~ans 这一行的状态,第三重 z=0~ans 上一行的状态 第四重 l=0~ans 上上行的状态
如果状态转移是合法的:dp[i][j][z]=max(dp[i][j][z],dp[i-1][z][l]+num[j])
最后答案总结也是两重 i=0~ans , j=0~ans枚举DP[raw][i][j]中的i,j
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=110;
const int INF=0x3fffffff;
typedef long long LL;
int dp[maxn][maxn][maxn];
//DP[raw][i][j] : 在第 raw 行状态为 i, 第 raw - 1 行状态为 j 的情况
int gra[maxn];
int n,m,ans;
int sta[maxn]; //合法状态
int num[maxn]; //这个合法状态里面的炮兵数量
bool check(int x){
// 推断该状态左右相邻两个单位是否有炮兵冲突
if(x&(x<<1)) return 0;
if(x&(x<<2)) return 0;
return 1;
}
// 计算比特位里的 1 的个数
int js(int x){
int cn=0;
while(x){
if(x&1) cn++;
x>>=1;
}
return cn;
}
/* 另一种得到个数的写法
int getsum(int x){
int sum=0;
while(x){
sum++;
x&=(x-1);
}
return sum;
}
*/
// 预处理,统计下全部“行”摆放炮兵的合法状态
void pre(){
memset(dp,-1,sizeof(dp));
memset(gra,0,sizeof(gra));
int stat=(1<<m);
for(int i=0;i<stat;i++){
if(check(i)){
sta[ans]=i;
num[ans]=js(i);
ans++;
}
}
}
int main(){
cin>>n>>m;
pre();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
char c;
cin>>c;
if(c=='H') gra[i]|=(1<<j); //保留这一行的状态
}
}
for(int i=0;i<ans;i++){
if(!(sta[i]&gra[0])) dp[0][i][0]=num[i]; //第一行状态为i时,可以有的数量
} //初始化第一行的状态
for(int i=1;i<n;i++){
for(int j=0;j<ans;j++){ //这一行
if(sta[j]&gra[i]) continue; //有重叠,第j个状态 和原本的图
for(int z=0;z<ans;z++){ //上一行
if(sta[j]&sta[z]) continue; //还是有重叠
for(int l=0;l<ans;l++){ //上上一行
if(sta[z]&sta[l]) continue; //重叠
if(sta[l]&sta[j]) continue;
dp[i][j][z]=max(dp[i][j][z],dp[i-1][z][l]+num[j]); //
//在两种情况里面取最大的
//要么在这里不弄,要么在这里弄,就加上值
}
}
}
}
int tot=0;
for(int i=0;i<ans;i++) {
for(int j=0;j<ans;j++){
tot=max(tot,dp[n-1][i][j]);
}
}
cout<<tot<<endl;
return 0;
}
1596:动物园
好难哦,读读原题吧:http://ybt.ssoier.cn:8088/problem_show.php?pid=1596
dp[i][s]表示从第i个位置往后数五个位置的状态是s时最多能有几个小朋友开心(0表示移走,1表示保留)
之后我们处理处每一个人的喜欢和害怕的状态,往下转移就好了
还有这是一个环,感觉非常不好处理的样子
我们可以枚举第一个位置之后的状态是什么,最后的位置必须和第一个位置吻合就好了
复杂度O(45n)
还是不太懂
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<queue>
#include<map>
#include<vector>
#include<set>
using namespace std;
const int maxn=50010;
const int INF=0x3fffffff;
typedef long long LL;
/*
好难啊
dp[i][s]表示从第i个位置往后数五个位置的状态是s时最多能有几个小朋友开心(0表示移走,1表示保留)
之后我们处理处每一个人的喜欢和害怕的状态,往下转移就好了
还有这是一个环,感觉非常不好处理的样子
我们可以枚举第一个位置之后的状态是什么,最后的位置必须和第一个位置吻合就好了
复杂度O(45n)
*/
int dp[10050][40];
int S[maxn]; //位置
int F[maxn]; //记录不喜欢的
int L[maxn]; //记录喜欢的
int n,c,e,f,l;
int ans=-1;
int main(){
int x;
scanf("%d %d",&n,&c);
for(int i=1;i<=c;i++){
scanf("%d",&S[i]);
scanf("%d %d",&f,&l);
F[i]=31; //因为时需要存储讨厌的动物的合理方案,所以先赋值为全1
for(int j=1;j<=f;j++){
scanf("%d",&x);
x-=S[i];
if(x<0) x+=n;
F[i]^=(1<<x); //讨厌的
}
for(int j=1;j<=l;j++){
scanf("%d",&x);
x-=S[i];
if(x<0) x+=n;
L[i]|=(1<<x); //喜欢的
}
}
for(int s=0;s<32;s++){ //对所有的合理的方案
memset(dp,-1,sizeof(dp));
int now=1;
for(int i=0;i<32;i++) dp[1][i]=-INF;
dp[1][s]=0;
while(S[now]==1){ //初始化开头??
if((L[now]&s)||((F[now]|s)!=31)) dp[1][s]++; //多了一个快乐的人
now++;
}
for(int i=1;i<n;i++){
for(int j=0;j<32;j++){
//从上一个门转移过来
dp[i+1][(j>>1)|(1<<4)]=max(dp[i][j],dp[i+1][(j>>1)|(1<<4)]) ;//留着
dp[i+1][j>>1]=max(dp[i][j],dp[i+1][j>>1]); //不管,不留下
}
while(S[now]==i+1){
for(int j=0;j<32;j++){
if((L[now]&j)||((F[now]|j)!=31)) dp[i+1][j]++; //如果这个状态能够让人满意
}
now++;
}
}
int t=s;
t^=(1<<4);
if(t>s) t-=(1<<4);
for(int i=0;i<32;i++) if((i>>1)==t) ans=max(ans,dp[n][i]);
}
printf("%d
",ans);
return 0;
}