C#数据结构_树

树的定义是递归的，用树来定义树。因此，树（以及二叉 树）的许多算法都使用了递归。

结点(Node)：表示树中的数据元素。

结点的度(Degree of Node)：结点所拥有的子树的个数。

树的度(Degree of Tree)：树中各结点度的最大值。

叶子结点(Leaf  Node)：度为 0 的结点，也叫终端结点。

结点的层次(Level of Node)：从根结点到树中某结点所经路径上的分支 数称为该结点的层次。根结点的层次规定为 1，其余结点的层次等于其双亲结点 的层次加 1。

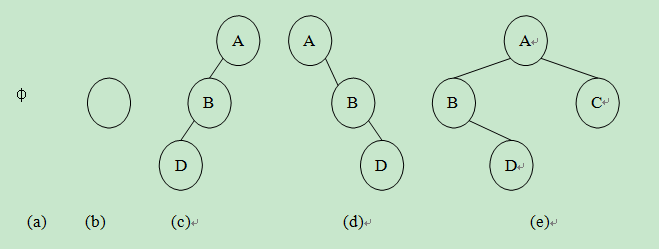
二叉树的形态共有 5 种：空二叉树、只有根结点的二叉树、右子树为空的二 叉树、左子树为空的二叉树和左、右子树非空的二叉树。

满二叉树(Full Binary Tree)：如果一棵二叉树只有度为 0 的结点和度为 2 的结点，并且度为 0 的结点在同一层上。

完全二叉树(Complete Binary Tree)：深度为 k，有 n 个结点的二叉树当且仅当其每一个结点都与深度为 k，有 n 个结点的满二叉树中编号从1到n 的结点一一对应时

 

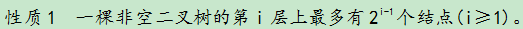
二叉树的二叉链表存储结构：一个数据域和两个引用域。

不带头结点的 二叉树的二叉链表的类 BiTree<T>类的实现：

    public class BiTree<T>
    {
        private Node<T> head;    //头引用

        //头引用属性
        public Node<T> Head
        {
            get{return head;}
            set{head=value;}
        }
        //构造器
        public BiTree()
        {
            head = null;
        }
        //构造器
        public BiTree(T val)
        {
            Node<T> p = new Node<T>(val);
            head = p;
        }
        //构造器
        public BiTree(T val, Node<T> lp, Node<T> rp)
        {
            Node<T> p = new Node<T>(val,lp,rp);
            head = p;
        }
        //判断是否是空二叉树
        public bool IsEmpty()
        {
            if (head == null)
            {
                return true;
            }
            else
            {
                return false;
            }
        }
        //获取根结点
        public Node<T> Root()
        {
            return head;
        }
        //获取结点的左孩子结点
        public Node<T> GetLChild(Node<T> p)
        {
            return p.LChild;
        }
        //获取结点的右孩子结点
        public Node<T> GetRChild(Node<T> p)
        {
            return p.RChild;
        }
        //将结点p的左子树插入值为val的新结点，原来的左子树成为新结点的左子树
        public void InsertL(T val, Node<T> p)
        {
            Node<T> tmp = new Node<T>(val);
            tmp.LChild = p.LChild;
            p.LChild = tmp;
        }
        //将结点p的右子树插入值为val的新结点，原来的右子树成为新结点的右子树
        public void InsertR(T val, Node<T> p)
        {
            Node<T> tmp = new Node<T>(val);
            tmp.RChild = p.RChild;
            p.RChild = tmp;
        }
        //若p非空，删除p的左子树
        public Node<T> DeleteL(Node<T> p)
        {
            if ((p == null) || (p.LChild == null))
            {
                return null;
            }
            Node<T> tmp = p.LChild;
            p.LChild = null;
            return tmp;
        }
        //若p非空，删除p的右子树
        public Node<T> DeleteR(Node<T> p)
        {
            if ((p == null) || (p.RChild == null))
            {
                return null;
            }
            Node<T> tmp = p.RChild;
            p.RChild = null;
            return tmp;
        }
        //判断是否是叶子结点
        public bool IsLeaf(Node<T> p)
        {
            if ((p != null) && (p.LChild == null) && (p.RChild == null))
            {
                return true;
            }
            else
            {
                return false;
            }
        }
    

二叉树的遍历：DLR（先序遍历）、LDR（中序遍历）和 LRD（后序遍历），层序遍历(Level Order)。

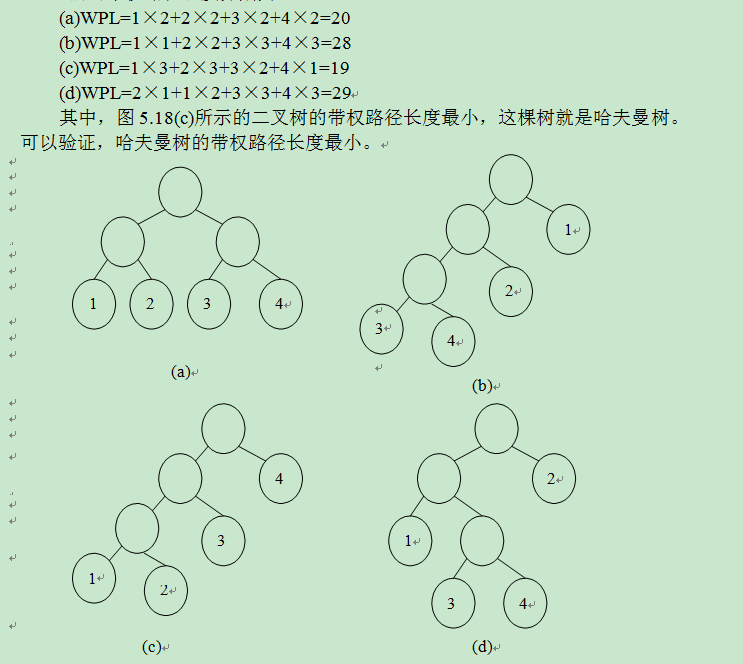
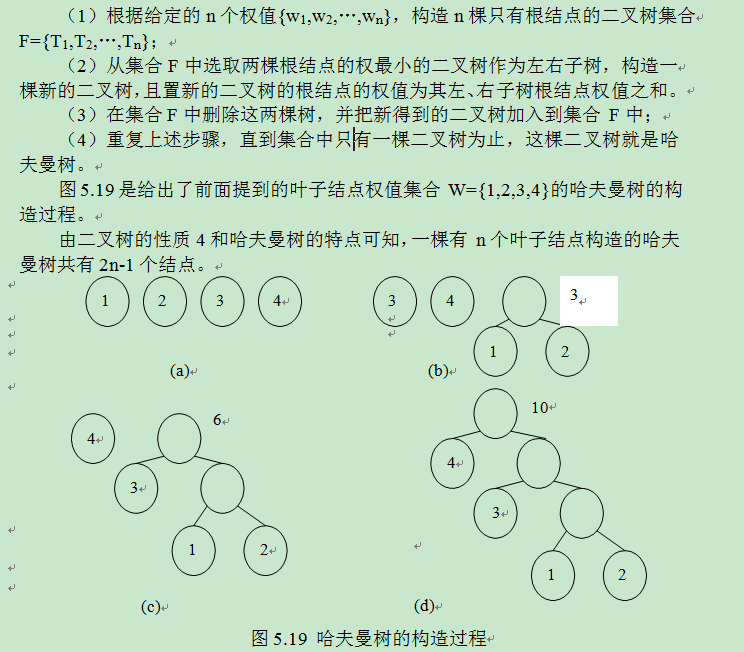
哈夫曼树(Huffman  Tree)，又叫最优二叉树，指的是对于一组具有确定权值 的叶子结点的具有最小带权路径长度的二叉树。