Arpa is researching the Mexican wave.
There are n spectators in the stadium, labeled from 1 to n. They start the Mexican wave at time 0.
- At time 1, the first spectator stands.
- At time 2, the second spectator stands.
- ...
- At time k, the k-th spectator stands.
- At time k + 1, the (k + 1)-th spectator stands and the first spectator sits.
- At time k + 2, the (k + 2)-th spectator stands and the second spectator sits.
- ...
- At time n, the n-th spectator stands and the (n - k)-th spectator sits.
- At time n + 1, the (n + 1 - k)-th spectator sits.
- ...
- At time n + k, the n-th spectator sits.
Arpa wants to know how many spectators are standing at time t.
The first line contains three integers n, k, t (1 ≤ n ≤ 109, 1 ≤ k ≤ n, 1 ≤ t < n + k).
Print single integer: how many spectators are standing at time t.
10 5 3
3
10 5 7
5
10 5 12
3
In the following a sitting spectator is represented as -, a standing spectator is represented as ^.
- At t = 0 ----------
 number of standing spectators = 0.
number of standing spectators = 0. - At t = 1 ^---------
 number of standing spectators = 1.
number of standing spectators = 1. - At t = 2 ^^--------
 number of standing spectators = 2.
number of standing spectators = 2. - At t = 3 ^^^-------
 number of standing spectators = 3.
number of standing spectators = 3. - At t = 4 ^^^^------
 number of standing spectators = 4.
number of standing spectators = 4. - At t = 5 ^^^^^-----
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 6 -^^^^^----
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 7 --^^^^^---
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 8 ---^^^^^--
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 9 ----^^^^^-
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 10 -----^^^^^
 number of standing spectators = 5.
number of standing spectators = 5. - At t = 11 ------^^^^
 number of standing spectators = 4.
number of standing spectators = 4. - At t = 12 -------^^^
 number of standing spectators = 3.
number of standing spectators = 3. - At t = 13 --------^^
 number of standing spectators = 2.
number of standing spectators = 2. - At t = 14 ---------^
 number of standing spectators = 1.
number of standing spectators = 1. - At t = 15 ----------
 number of standing spectators = 0.
number of standing spectators = 0.
分情况讨论
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #define lowbit(x) (x&(-x)) #define max(x,y) (x>y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.141592653589793238462 #define ios() ios::sync_with_stdio(false) #define INF 1044266558 #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; int n,m,k; int main() { scanf("%d%d%d",&n,&m,&k); if(k>=0 && k<=m) printf("%d ",k); else if(k>m && k<=n) printf("%d ",m); else if(k>n && k<=n+m) printf("%d ",m-k+n); else printf("0 "); return 0; }
Arpa is taking a geometry exam. Here is the last problem of the exam.
You are given three points a, b, c.
Find a point and an angle such that if we rotate the page around the point by the angle, the new position of a is the same as the old position of b, and the new position of b is the same as the old position of c.
Arpa is doubting if the problem has a solution or not (i.e. if there exists a point and an angle satisfying the condition). Help Arpa determine if the question has a solution or not.
The only line contains six integers ax, ay, bx, by, cx, cy (|ax|, |ay|, |bx|, |by|, |cx|, |cy| ≤ 109). It's guaranteed that the points are distinct.
Print "Yes" if the problem has a solution, "No" otherwise.
You can print each letter in any case (upper or lower).
三点共线一定不存在,除此之外,若a到b的距离等于b到c的距离存在。
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #define lowbit(x) (x&(-x)) #define max(x,y) (x>y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.141592653589793238462 #define ios() ios::sync_with_stdio(false) #define INF 1044266558 #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; struct point { ll x; ll y; }node[4]; ll dist(point a,point b) { return ((a.y-b.y)*(a.y-b.y))+((a.x-b.x)*(a.x-b.x)); } bool check() { int ans=0; if(dist(node[1],node[0])==dist(node[1],node[2])) ans=1; if(ans) return true; else return false; } bool solve() { double a=((node[1].y-node[0].y)*1.0)/((node[1].x-node[0].x)*1.0); double b=((node[2].y-node[0].y)*1.0)/((node[2].x-node[0].x)*1.0); if(a==b) return true; return false; } int main() { for(int i=0;i<3;i++) { scanf("%lld%lld",&node[i].x,&node[i].y); } if(solve()) puts("No"); else if(check()) puts("Yes"); else puts("No"); return 0; }
You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.
We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 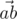 and
and 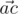 is acute (i.e. strictly less than
is acute (i.e. strictly less than 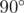 ). Otherwise, the point is called good.
). Otherwise, the point is called good.
The angle between vectors 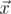 and
and 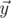 in 5-dimensional space is defined as
in 5-dimensional space is defined as 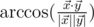 , where
, where 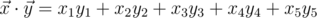 is the scalar product and
is the scalar product and 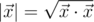 is length of
is length of 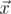 .
.
Given the list of points, print the indices of the good points in ascending order.
The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.
The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — the coordinates of the i-th point. All points are distinct.
First, print a single integer k — the number of good points.
Then, print k integers, each on their own line — the indices of the good points in ascending order.
6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1
1
3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0
0
In the first sample, the first point forms exactly a 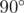 angle with all other pairs of points, so it is good.
angle with all other pairs of points, so it is good.
In the second sample, along the cd plane, we can see the points look as follows:
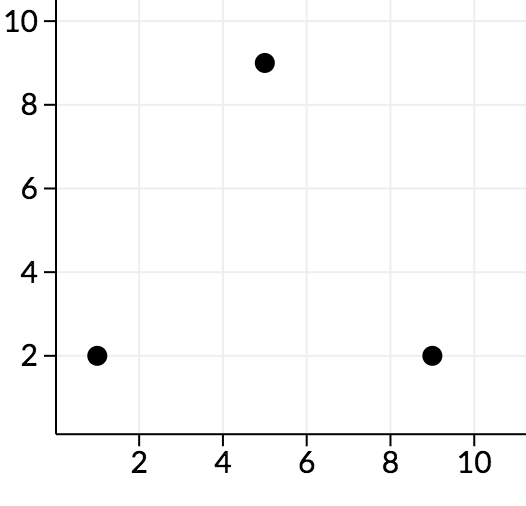
We can see that all angles here are acute, so no points are good.
暴力枚举
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #define lowbit(x) (x&(-x)) #define max(x,y) (x>y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.141592653589793238462 #define ios() ios::sync_with_stdio(false) #define INF 1044266558 #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; ll a[1006][6]; int n,vis[1003]; set<ll>s; bool check(int x,int y,int z) { ll pos=0; for(int i=0;i<5;i++) pos+=(a[y][i]-a[x][i])*(a[z][i]-a[x][i]); if(pos>0) return false; return true; } int main() { scanf("%d",&n); for(int i=0;i<n;i++) { s.insert(i+1); for(int j=0;j<5;j++) scanf("%lld",&a[i][j]); } int l=n; for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { for(int k=j+1;k<n;k++) { if(i!=j && i!=k) { if(!check(i,j,k)) { l--; s.erase(i+1); goto eg; } } } } eg:; } printf("%d ",l); if(s.size()) { for(set<ll>::iterator it=s.begin();it!=s.end();it++) { printf("%lld ",*it); } } return 0; }