高斯函数与高斯滤波
一维高斯函数我们都熟悉,形式如下:
计算机视觉中,高斯滤波使用的高斯核为(x)和(y)两个一维高斯的乘积,两个维度上的标准差(sigma)通常相同,形式如下:
高斯滤波(平滑),即用某一尺寸的二维高斯核与图像进行卷积。高斯核是对连续高斯函数的离散近似,通常对高斯曲面进行离散采样和归一化得出,这里,归一化指的是卷积核所有元素之和为1,下图为标准高斯和(sigma=1.4)大小为(5 imes5)的高斯核。
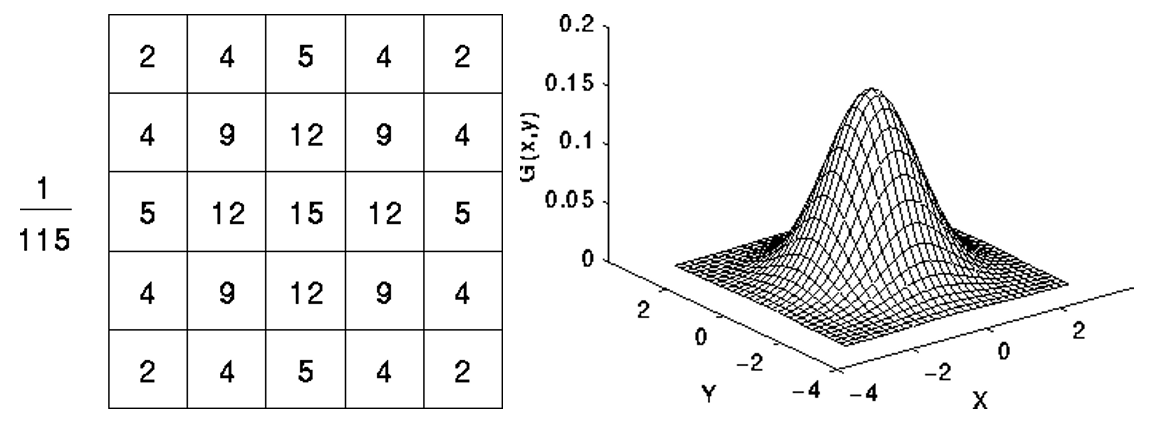
标准差
当(mu=0)时,唯一需要控制的参数就是标准差(sigma),多少合适呢?(sigma)的确定十分依赖于问题背景,需要具体问题具体分析。但理解(sigma)的作用,可以指导调整的方向。
高斯核可以看成是与中心距离负相关的权重。平滑时,调整(sigma)实际是在调整周围像素对当前像素的影响程度,调大(sigma)即提高了远处像素对中心像素的影响程度,滤波结果也就越平滑。高斯曲线随(sigma)变化的曲线如下:
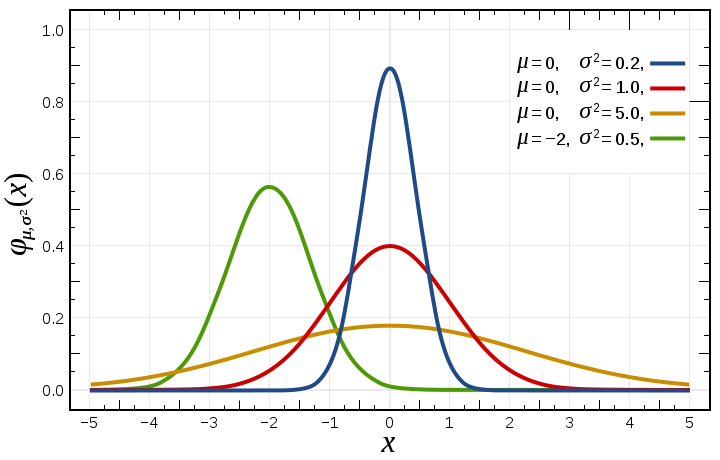
从频域角度看,高斯函数的傅立叶变换仍是高斯,两者标准差间的关系如下:
其中,(sigma_x)为空域高斯的标准差,(sigma_w)为对应频域高斯的标准差,在空域进行高斯平滑相当于频域低通滤波,(sigma_x)越大,(sigma_w)越小,频域高斯越集中,高频成分削弱得越多,图像越平滑。
从低通滤波角度考虑,可以对图像做傅立叶变换进行频谱分析,叠加上频域高斯并调整查看效果,找到适合的(sigma_w),再推算出空域高斯所需的(sigma_x)。
窗口大小
标准差(sigma)确定后,接下来需要确定窗口大小。上面讲了高斯核是对连续高斯的离散近似,窗口越大自然近似越好,但高斯函数是钟形曲线,距离中心越远数值越小,足够远处可以忽略不计,但多远算远呢?
钟型曲线在区间((mu - sigma, mu +sigma))范围内的面积占曲线下总面积的(68\%),((mu - 2sigma, mu +2sigma))范围占(95\%),((mu - 3sigma, mu +3sigma))范围占(99.7\%),一般(3sigma)外的数值已接近于0,可忽略,半径为(3sigma)即窗口大小为(6sigma imes 6sigma)即可,通常取最近的奇数。上述3个范围在一维和二维高斯中示意如下:
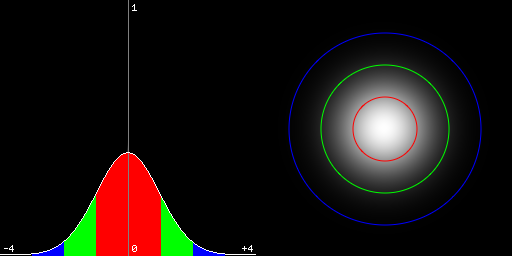
OpenCV中标准差与窗口大小的换算
在OpenCV函数createGaussianFilter中,若未指定窗口大小,通过(sigma)推算窗口大小方式如下,半径为(sigma)的3或4倍:

若指定了窗口大小,但未指定(sigma)大小,则通过窗口大小推算(sigma)的方式如下:
具体地,在函数getGaussianKernel中,当ksize不大于7时,直接从内部的small_gaussian_tab取对应大小的高斯核,若大于7,则使用上式计算出(sigma)然后套用高斯公式,最后再归一化。
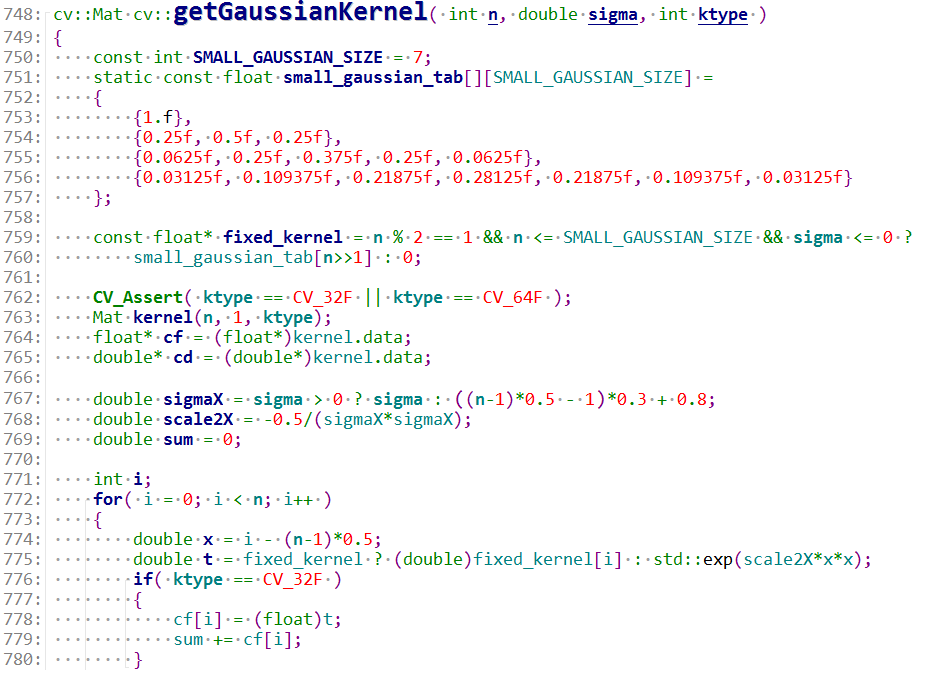
在实际使用时,为了高效,卷积核通常取([0, 255])范围内的整数(1个Byte),因此高斯核中心最大取值为255时,窗口尺寸的选取只需让高斯核边界值刚好大于0即可。令高斯核尺寸为(n),半径为(r),(r = frac{n-1}{2}),高斯核(x)轴上边界((r, 0))处与中心((0, 0))处数值之比如下:
当(r)足够大,其极限为(exp(-frac{1}{2 imes0.3^2})=0.00386592),若中心值为255,则边界值为(255*0.00386592=0.9858096 approx 1),是合适的。但公式是如何设计出来的还不清楚,这里只是校验了其性质,sigh。
参考
- getGaussianKernel
- Calculate the Gaussian filter's sigma using the kernel's size
- Gaussian blur
- Gaussian Blur - Standard Deviation, Radius and Kernel Size
- How to determine the window size of a Gaussian filter
- Optimal Gaussian filter radius
- Fast Almost-Gaussian Filtering
- Gaussian Smoothing
本文出自本人博客:如何确定高斯滤波的标准差和窗口大小