1 import numpy as np 2 import pandas as pd 3 import seaborn as sns 4 import matplotlib.pyplot as plt 5 %matplotlib inline 6 7 plt.rcParams['font.sans-serif']=['Simhei'] 8 plt.rcParams['axes.unicode_minus']=False
1 np.__version__
'1.19.1'
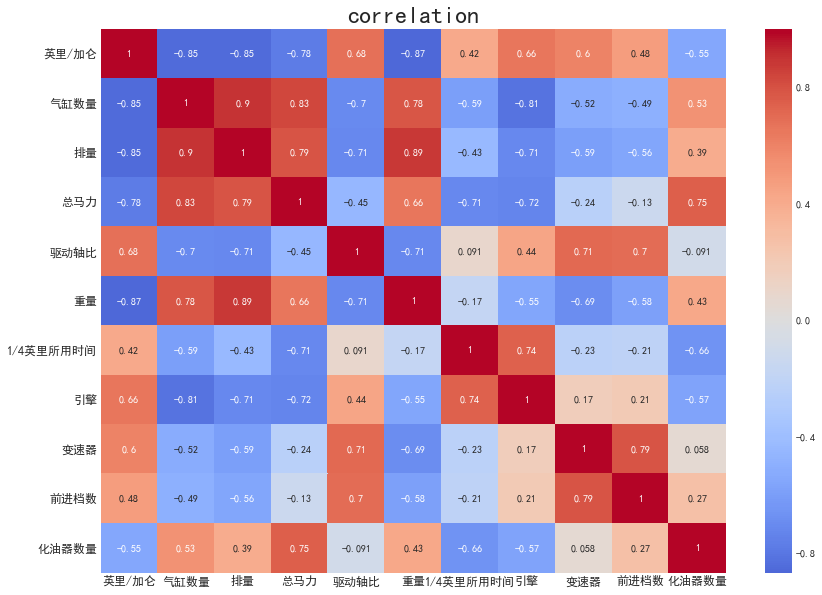
2.相关矩阵图
相关矩阵图的目的是探索两个事物之间的关系。实际应用中,我们常常需要探索多个变量的两两之间的相关性。
相关系数:绝对值越接近1,相关性越强,1指的是完全正相关,-1指的是完全负相关,0表示完全无关
1 plt.style.use('seaborn-whitegrid') 2 sns.set_style('white') 3 xg_data = pd.read_excel('可视化图表案例数据.xlsx',sheet_name='相关矩阵图') 4 xg_data.head(3)
| Unnamed: 0 | 英里/加仑 | 气缸数量 | 排量 | 总马力 | 驱动轴比 | 重量 | 1/4英里所用时间 | 引擎 | 变速器 | 前进档数 | 化油器数量 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Mazda RX4 | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 |
| 1 | Mazda RX4 Wag | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 |
| 2 | Datsun 710 | 22.8 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 |
实现相关性矩阵
1 chuli_data = xg_data.corr() 2 chuli_data.shape
(11, 11)
1 np.zeros((11,11))
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
1 plt.rcParams['font.sans-serif']=['Simhei'] 2 plt.rcParams['axes.unicode_minus']=False 3 4 plt.figure(figsize=(14,10)) 5 6 sns.heatmap(chuli_data, #相关性矩阵所需要的数据 7 #xticklabels=chuli_data.columns, #横坐标标签 8 #yticklabels=chuli_data.columns, #纵坐标标签 9 cmap='coolwarm', #使用的光谱 10 center = 0, #cneter:数据的中值,越靠近两端的值,颜色越接近于对应设定值 11 annot=True) 12 13 plt.title('correlation',fontsize=24) 14 15 plt.xticks(fontsize=12) 16 plt.yticks(fontsize=12) 17 18 plt.show()