机器学习

线性回归建模

数据集

结构

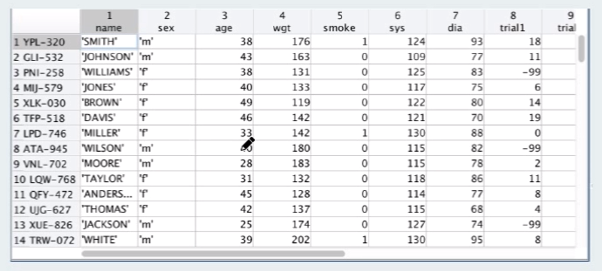
简述 

存在

　　name - 姓名

　　sex - 性别

　　wgt - 体重

　　smoke - 是否吸烟

预测

　　sys - 收缩压

建模

训练, 预测

 表示一个训练样本, x 表示输入, y 表示输出, 训练数据的 x , y 都是给定的现有数据

 则表示训练样本集, 1....N 表示有 N 个样本

当然每个样本可能存在多个特征对结果 y 的影响因素

因此将其简化为 粗体的 X , X 以向量的形式展示, 内部存放多维度的特征值 

于此得到的模型为 输入一个 X^# , X^#内部存在多个特征值, 然后期望获得一个 y^# 的预测结果

线性模型

将模型转化成线性模型的方式, 线性模型作为最经典最简单的模型也是最适用的模型

日后当然也可以使用更复杂的模型, 这里线性模型基本上就可以满足我们的要求实现我们的目的

标量的情况, 拟定的线性方程, 使得每一个原始数据 X⁽ⁱ⁾ 的输出 y⁽ⁱ⁾ 的输出近似于真实的 y⁽ⁱ⁾ 

      ω 是系数, 而 b 为偏置 

向量的情况则是这样,  拟定的线性方程, 则是输入的向量进行转置后乘以一个向量 , 既内积

      w^T 是系数, 而 b 为偏置 

最终的结果也是一个标量 , 于此, 这里的问题就是怎么找出这个 ω / w^T 以及 b 

简单总结

简化为标量线性模型, 转化为向量线性模型, 缺失参数和偏置,

需要怎么样的学习方式才可以得出这个正确的 参数和偏置项, 就是我们要解决的问题

无约束优化分析法

接着上面的建模遇到的问题继续走

本质上这就是个无约束优化问题

所谓的无约束优化问题即是

无约束优化问题

本质上就是一个求极值点的问题

对于代数问题的话即使简单的代入算出即可, 但是对于向量的多维则较为复杂

可以使用 Countour 的方法来处理, 如图就是 输入 x, y 得出 z 的图示, 

按照每个 z 进行切平面. 下面的环形投影的分析就较为方便

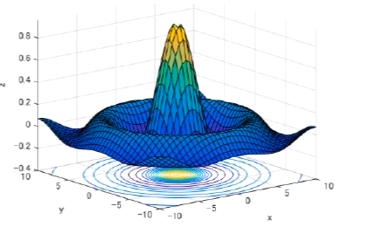
但是超多维度的时候的处理会更为复杂, 因此只能在代数上解决此类问题, 而可视化是很难的体现

极值点的情况当然也很多, 可以局部可以全局, 因此延续上面的问题转变成了求极值问题

梯度和Hessian 矩阵

既然是求某一个形状的方程式, 那就需要计算的它的扭曲方式或者射出方位,

这需要用到导数, 导数本质上就是求切线, 速度等定义, 这样就可以计算出他的形状

因此引入梯度的概念

一阶导数和梯度的一个简单的举例,

  输入的是两维的, 输出的也是两维的向量

大部分情况 用来表示梯度,. 为了简单更喜欢用 g(x) 来表示梯度

二阶导数既在一阶求导后再求导,

例如 x² -> 2x -> 2 

如果是向量的话, 二阶导数就会成为 海森矩阵 

本质上 海森矩阵是个对称矩阵 

基于上面的 z = x² + y² 的例子

一阶导数的结果是

  

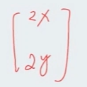
再进行二次求导的结果就是 

 海森矩阵一般写成 H(x) 的形式

二次型

仅仅这些还不够要用到二次型

二次型的例子: 

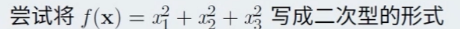
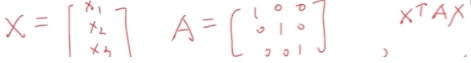
这里根据定义即可发现, 对于所有的对称矩阵都可以判定正(定矩阵)负(定矩阵) 

而且正负矩阵也对特征进行了明确

因此前面说的 海森矩阵本身作为对称矩阵既可以进行正负的判定

具体计算

在有了上面的前提下才可以进行计算

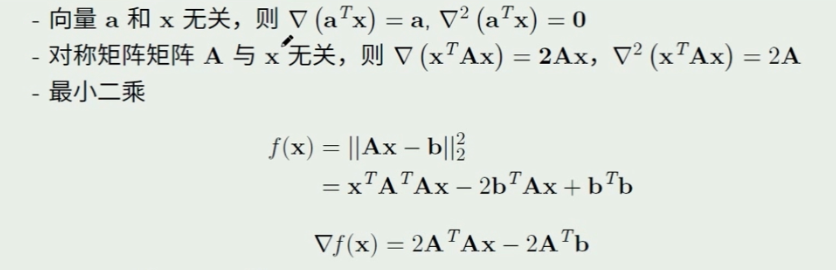
具体的计算

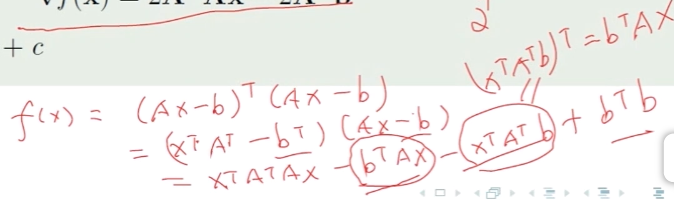
最终的梯度结果即是个二次型

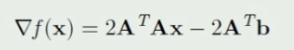
泰勒级数

得到了梯度后, 进行函数的分析,这时候需要用到泰勒展开

既可以看出 , 一阶导数就是梯度, 二阶导数就是 海森矩阵的那那个二次型

当然还有三阶导数四阶导数等等, 但是对于这里的使用已经足够了. 二阶足以

标量情况的计算

 

根据泰勒展开的算法 得到的公式 

 + δ 可正可负, 表示左右移动,

而所谓严格局部最小点即是左右的点都要被这个点大

既然要求别的位置都要大于极小点, 那么结合式子来看 

姑且忽略后面的二阶项, 那么一阶项  就必须要作为一个正数才可以保证  比  大

于是这样让一阶项  = 0 的点就叫做平稳点 (候选点) 此时的情况分为三种 : 极大, 极小, 鞍店

至此还是无法确定最小点, 所以这里使用到二阶项

根据上面的分析, 一阶项等于0了. 要满足   比  大 , 因此二阶项 就要大于0  

这里  δ² 必然大于0 了, 所以推出   一定大于 0 

最终结论

如果一个函数存在严格的局部极小点

那么在这个点上 一阶项一定为 0 , 二阶项一定大于 0

因此计算方式具体为

　　- 先用 一阶导 = 0 来筛选出候选点

　　- 再用 二阶导 > 0 判定极小点

ps :

　　如果 二阶导数也 0 那就只能再用三阶导数来继续判断

　　比方来说 x³ 的一阶 = 0 的时候, 二阶就也是 = 0 

　　还是那句话, 大部分的情况下, 二阶导数完全足够了

向量情况的计算

了解了标量的情况下在理解变量就较为容易

梯度 g(x) = 0  的情况下就是平稳点

海森矩阵 H(x)  正定 的话就是严格局部极小点

梯度为0求解的局限性

前面的一切的最终结果就是转化成代数问题求解方程

对于函数的性质很友好的时候求导是很容易的, 不如 f(x) = x² 这样的函数求导容易而且一下子就求出了全局极小点

但是对于复杂函数求导数在很多时候是很蛋疼的一件事

比如下面的例子

如果是多元的将会更加复杂难解, 甚至不可解. 因此可见有约束迭代法还是有所局限

因此这类问题我们需要用到无约束迭代法

无约束迭代法

优化迭代法基本结构

  

d_k 方向的不同是不同迭代方法的主要区分, 而  d_k  的不同也会严重的影响到迭代次数 k , d_k 的方向选择很重要, 将会直接影响到下降速度

步长 α_k 也经常被叫做 学习率 , 每一次的顺着方向的下降对模型进行更新

更新不可能无止境的继续下去, 需要一个停止准则, 作为局部极小点的判断依据

方向

梯度下降法

推导

深度, 梯度下降法是最常见的一种 方向选择的公式为 

这里的公式的推导姑且忽略掉 α_k 的影响, 以及二次项  得到的公式为 

为了满足下降的程度  最快, 因此需要   为一个负数. 而且越大( 绝对值越大 )的负数越好 

按照两个向量的内积公式, 两个向量的内积就是两个向量的 || ||₂ 的乘机乘以他们的向量角度

而 cosΘ 的取值是  -1 <= cosΘ  <=1 ,  || ||₂ 肯定是个正数 , 因此这样  cosΘ 就要等于 -1 即 180° 的反方向

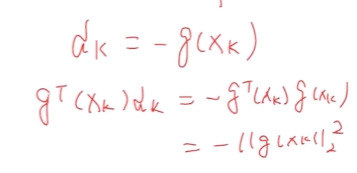
这样就得出了   的目标函数

弊端

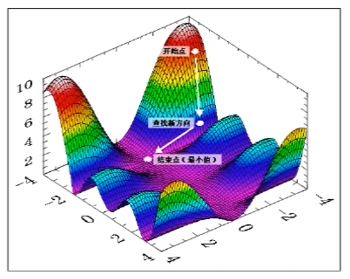
对于这样的测试方式也存在初始点选取不当的时候无法下降到真正的极值点的情况比如下图这样复杂函数

因此需要多个初始点进行比对选取

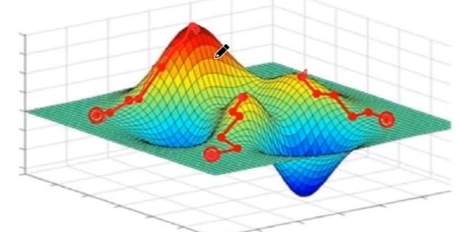
梯度下降法是基于一阶导的方向作为依据进行的, 在保留了一阶项的情况下梯度下降法是最优方法

但是考虑二阶三阶项等的时候则不必然

牛顿法

 对比梯度下降法的省略掉二阶项, 牛顿法加上了二阶项, 会有更好的精度

推导

 

对于这个目标程式, 唯一不知道的 项就是 d_k , 这里将 ≈ 近似处理成 = 了, 为了满足 = , 于是 d_k 的取值需要计算出来

对  d_k 求导, 从而先解出来  d_{k  -----} 

 和 d_k 没关系求导 = 0,  根据  ,   的求导就是  ,  的求导则是 

得到 ,   在要求海森矩阵正定的情况下解出  

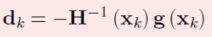
弊端

矩阵的求逆是更复杂的操作, 以及求逆是很不稳定的, 工程中应尽量避免

而且牛顿法的方法只适用于海森矩阵正定的情况, 如果是不定矩阵或者浮动则需要进行修正才可以. 或者使用拟牛顿法来解决

拟牛顿法

梯度下降和牛顿法的之间是否可以找到一个比梯度下降更快,但是又能弥补牛顿法的弊端的算法?

那么将两种进行统合一下成这个式子    

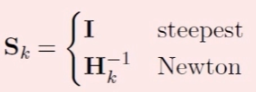
其中  对应的是梯度下降,  对应的是牛顿法

为了避免牛顿的求矩阵的逆这样不稳定的结果, 所以我们尝试用一正定矩阵去逼近从而求解出一个近似的逆

那么要找那个正定矩阵从而让求的值最近似与期望的逆就是个问题,  同时需要满足条件

  , 

有两种方法可以进行计算 DFP , BFGS

 DFP

 

这里的算法较为复杂, 其实化解来看就是在满足前面的那个前提条件下的解方程 

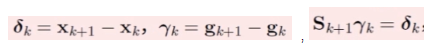
在此前提下, 我们设定 

未知变量调整为 1 和 -1 从而化简成为  

最后求解, 具体过程不需要太追究, 日常使用还是掉包即可, 重点在于理解思想 

BFGS

 当然可以设定为其他的形式, 由此可以得出 BFGS 算法, 详细的推导依旧不重要

BFGS 和 DFP 的本质上性能其实差别不大, 实际中更喜欢用 BFGS 算法, 在数值上可能相对更稳定一些

步长求取

线性回归求解