NOI2011 在吉林大学开始啦!为了迎接来自全国各地最优秀的信息学选手, 吉林大学决定举办两场盛大的 NOI 嘉年华活动,分在两个不同的地点举办。每 个嘉年华可能包含很多个活动,而每个活动只能在一个嘉年华中举办。 现在嘉年华活动的组织者小安一共收到了 n 个活动的举办申请,其中第 i 个 活动的起始时间为 Si,活动的持续时间为 Ti。这些活动都可以安排到任意一个嘉 年华的会场,也可以不安排。 小安通过广泛的调查发现,如果某个时刻,两个嘉年华会场同时有活动在进 行(不包括活动的开始瞬间和结束瞬间),那么有的选手就会纠结于到底去哪个 会场,从而变得不开心。所以,为了避免这样不开心的事情发生,小安要求不能 有两个活动在两个会场同时进行(同一会场内的活动可以任意进行)。 另外,可以想象,如果某一个嘉年华会场的活动太少,那么这个嘉年华的吸 引力就会不足,容易导致场面冷清。所以小安希望通过合理的安排,使得活动相 对较少的嘉年华的活动数量最大。 此外,有一些活动非常有意义,小安希望能举办,他希望知道,如果第 i 个 活动必须举办(可以安排在两场嘉年华中的任何一个),活动相对较少的嘉年华 的活动数量的最大值。
输入的第一行包含一个整数 n,表示申请的活动个数。 接下来 n 行描述所有活动,其中第 i 行包含两个整数 Si、Ti,表示第 i 个活 动从时刻 Si开始,持续 Ti的时间。
输出的第一行包含一个整数,表示在没有任何限制的情况下,活动较少的嘉 年华的活动数的最大值。 接下来 n 行每行一个整数,其中第 i 行的整数表示在必须选择第 i 个活动的 前提下,活动较少的嘉年华的活动数的最大值。
5
8 2
1 5
5 3
3 2
5 3
2
2
1
2
2
2
【样例说明】
在没有任何限制的情况下,最优安排可以在一个嘉年华安排活动 1, 4,而在 另一个嘉年华安排活动 3, 5,活动 2 不安排。
【数据规模与约定】
1≤n≤200
0≤Si≤109
1≤Ti≤ 109
先看这个大神的详细题解,这个写得真的很清晰很好懂啊!

然后说说那个什么递增单凸的。
首先,显然pre[][x]和suf[][y]都是递减的。
对于x确定,y在变,f[x][y]=min(x+y,pre[i][x]+num[i][j]+suf[j][y]),显然x+y随y递增而增,pre[i][x]+num[i][j]+suf[j][y]随y递增而减。
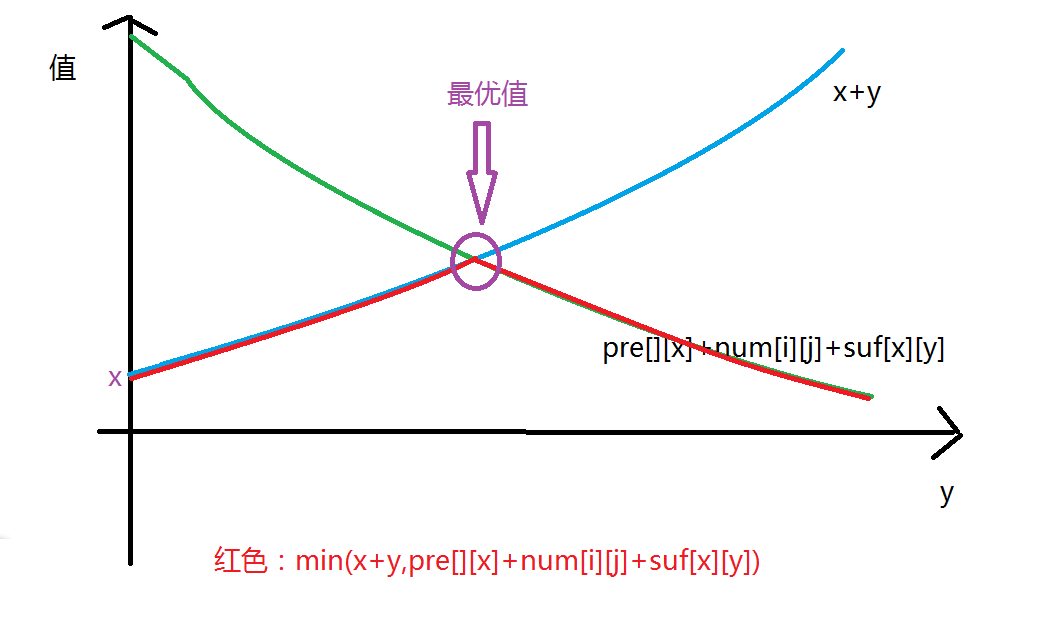
就是这样的,下面标红的函数就是真正的函数,显然是上凸的了。
所以程序里面y按顺序,找到一个now<当前最优值 就可以break了。
然后说明一个就是随着x的增加,取最优值的y单调递减。这个画个图也可以看出来了。

所以就是这样做了,y这里均摊的话,就是O(n^3) --引自Konjakmoyu
#include<cstdio> #include<algorithm> #include<iostream> using namespace std; const int N=401; const int inf=1e9; int n,p,ans,s[N],t[N]; struct node{int x,y;}a[N]; int num[N][N],pre[N][N],suf[N][N]; int g[N][N]; bool cmp(const node &a,const node &b){ return a.x<b.x; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d%d",&s[i],&t[i]);t[i]+=s[i]; a[i<<1].x=s[i];a[i<<1].y=i; a[i<<1|1].x=t[i];a[i<<1|1].y=-i; } sort(a+2,a+n*2+2,cmp); for(int i=2;i<=2*n+1;i++){ if(i==2||a[i].x!=a[i-1].x) p++; if(a[i].y>0) s[a[i].y]=p; else t[-a[i].y]=p; } for(int i=1;i<=p;i++){ for(int j=i;j<=p;j++){ for(int k=1;k<=n;k++){ if(s[k]>=i&&t[k]<=j){ num[i][j]++; } } } } for(int i=1;i<=p;i++){ for(int j=0;j<=n;j++){ if(j>num[1][i]){pre[i][j]=-inf;continue;} for(int k=0;k<=i;k++){ pre[i][j]=max(pre[i][j],pre[k][j]+num[k][i]); if(j-num[k][i]>=0) pre[i][j]=max(pre[i][j],pre[k][j-num[k][i]]); } } } for(int i=p;i>=1;i--){ for(int j=0;j<=n;j++){ if(j>num[i][p]){suf[i][j]=-inf;continue;} for(int k=i;k<=p;k++){ suf[i][j]=max(suf[i][j],suf[k][j]+num[i][k]); if(j-num[i][k]>=0) suf[i][j]=max(suf[i][j],suf[k][j-num[i][k]]); } } } for(int i=1,now,id;i<=p;i++){ for(int j=i;j<=p;j++){ int y=num[j][p]; for(int x=0;x<=num[1][i];x++){ for(;y>=0;y--){ now=min(x+y,pre[i][x]+num[i][j]+suf[j][y]); if(g[i][j]<=now){ g[i][j]=now; id=y; } else break; } y=id; } ans=max(ans,g[i][j]); } } for(int i=1;i<=p;i++){ for(int j=p;j>=i;j--){ g[i][j]=max(g[i][j],g[i][j+1]); } } for(int i=1;i<=p;i++){ for(int j=i;j<=p;j++){ g[i][j]=max(g[i][j],g[i-1][j]); } } printf("%d ",ans); for(int i=1;i<=n;i++) printf("%d ",g[s[i]][t[i]]); return 0; }