HDU 5306 Gorgeous Sequence[线段树区间最值操作]

Gorgeous Sequence

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 2150    Accepted Submission(s): 594

Problem Description

There is a sequence a of length n. We use ai to denote the i-th element in this sequence. You should do the following three types of operations to this sequence.

0 x y t: For every x≤i≤y, we use min(ai,t) to replace the original ai's value.
1 x y: Print the maximum value of ai that x≤i≤y.
2 x y: Print the sum of ai that x≤i≤y.

 

Input

The first line of the input is a single integer T, indicating the number of testcases. 

The first line contains two integers n and m denoting the length of the sequence and the number of operations.

The second line contains n separated integers a1,…,an (∀1≤i≤n,0≤ai<231).

Each of the following m lines represents one operation (1≤x≤y≤n,0≤t<231).

It is guaranteed that T=100, ∑n≤1000000, ∑m≤1000000.

 

Output

For every operation of type 1 or 2, print one line containing the answer to the corresponding query.

 

Sample Input

1 5 5 1 2 3 4 5 1 1 5 2 1 5 0 3 5 3 1 1 5 2 1 5

 

Sample Output

5 15 3 12

Hint

Please use efficient IO method

 

Author

XJZX

 

Source

2015 Multi-University Training Contest 2

 

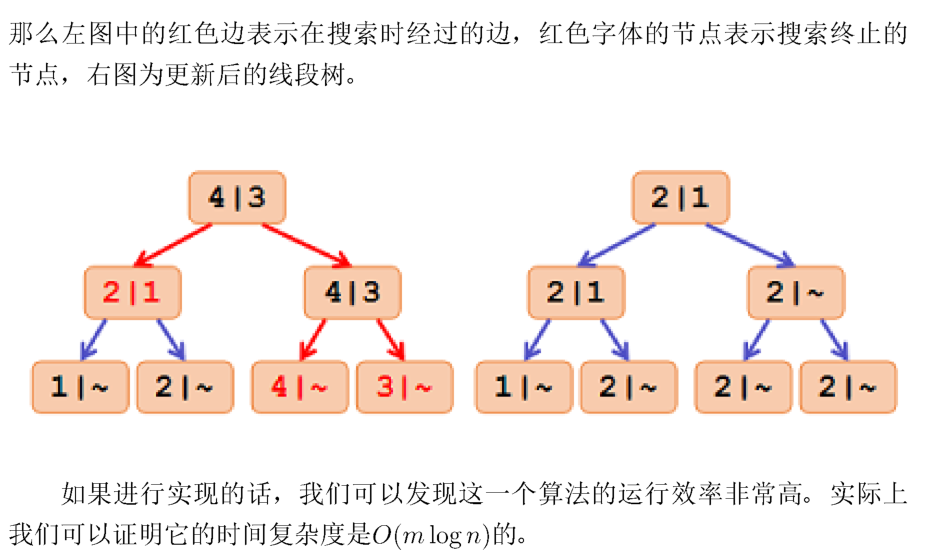
一份代码交了13遍。从TLE->WA->TLE->……QAQ

#include<cstdio>
#include<iostream>
#define lc k<<1
#define rc k<<1|1
#define EF if(ch==EOF) return x;
using namespace std;
typedef long long ll;
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;EF;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int N=1e6+5;
const int M=N<<2;
int n,m,a[N];
ll sum[M];int mx[M],se[M],mc[M];
inline void updata(int k){
    sum[k]=sum[lc]+sum[rc];
    mx[k]=max(mx[lc],mx[rc]);
    se[k]=max(se[lc],se[rc]);mc[k]=0;
    if(mx[lc]!=mx[rc]) se[k]=max(se[k],min(mx[lc],mx[rc]));
    if(mx[k]==mx[lc]) mc[k]+=mc[lc];
    if(mx[k]==mx[rc]) mc[k]+=mc[rc];
}
inline void dec_tag(int k,int v){
    if(v>=mx[k]) return ;
    sum[k]+=1LL*(v-mx[k])*mc[k];mx[k]=v;
}
inline void pushdown(int k){
    dec_tag(lc,mx[k]);
    dec_tag(rc,mx[k]);
}
void build(int k,int l,int r){
    if(l==r){
        sum[k]=mx[k]=a[l];mc[k]=1;se[k]=-1;
        return ;
    }
    int mid=l+r>>1;
    build(lc,l,mid);
    build(rc,mid+1,r);
    updata(k);
}
void change(int k,int l,int r,int x,int y,int v){
    if(v>=mx[k]) return ;
    if(l==x&&r==y&&v>se[k]){
        dec_tag(k,v);return ;
    }
    pushdown(k);
    int mid=l+r>>1;
    if(y<=mid) change(lc,l,mid,x,y,v);
    else if(x>mid) change(rc,mid+1,r,x,y,v);
    else change(lc,l,mid,x,mid,v),change(rc,mid+1,r,mid+1,y,v);
    updata(k);    
}
int query_max(int k,int l,int r,int x,int y){
    if(l==x&&r==y) return mx[k];
    pushdown(k);
    int mid=l+r>>1;
    if(y<=mid) return query_max(lc,l,mid,x,y);
    else if(x>mid) return query_max(rc,mid+1,r,x,y);
    else return max(query_max(lc,l,mid,x,mid),query_max(rc,mid+1,r,mid+1,y));
}
ll query_sum(int k,int l,int r,int x,int y){
    if(l==x&&r==y) return sum[k];
    pushdown(k);
    int mid=l+r>>1;
    if(y<=mid) return query_sum(lc,l,mid,x,y);
    else if(x>mid) return query_sum(rc,mid+1,r,x,y);
    else return query_sum(lc,l,mid,x,mid)+query_sum(rc,mid+1,r,mid+1,y);
}
inline void work(){
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    build(1,1,n);
    for(int i=1,opt,x,y,z;i<=m;i++){
        opt=read();x=read();y=read();
        if(opt==0) z=read(),change(1,1,n,x,y,z);
        if(opt==1) printf("%d
",query_max(1,1,n,x,y));
        if(opt==2) printf("%lld
",query_sum(1,1,n,x,y));
    }
}
int main(){
    for(int T=read();T--;) work();
    return 0;
}