287. 寻找重复数

题目描述

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

示例 1:

输入: [1,3,4,2,2]
输出: 2

示例 2:

输入: [3,1,3,4,2]
输出: 3

说明：

• 不能更改原数组（假设数组是只读的）。
• 只能使用额外的 O(1) 的空间。
• 时间复杂度小于 O(n2) 。
• 数组中只有一个重复的数字，但它可能不止重复出现一次。

题意

审题可以发现两个关键点：

1. nums数组长度为1+n，其中的数字范围皆介于[1,n]
2. 只有一个重复的数字，但是可能出现2次或以上

由第1点可知：对于任意下标1 <= i <= n, 总有1 <= nums[i] <= n，即将nums数组看为一个链表的话，是不会出现越界错误的。具体看为链表的方式是将nums[i]作为下一个元素的下标。

举个例子：
 nums = [1,3,4,2,2]，假设有个头节点head且值为0，链表可以整理为
 head->1->3->2->4->2->4->...
 head后面之所以为1是因为nums[0] = 1;同理，nums[1] = 3; nums[3] = 2;以此类推
 最后的省略号代表循环部分

由第2点可知：给出判断的nums数组形成的链表必有环，且为单环

算法

说到如何判断有环，以及寻找环的起点，常用的算法为快慢指针。

快慢指针的思想如下：

 声明两个指针，两个指针的初始值都是链表的头指针，让它们两同时出发，快指针每次前移两个节点，慢指针每次前移一个节点。

• 如果链表无环，那么两个指针永远不会相遇，也就是说当快指针抵达链表末尾，慢指针还在链表中间

• 如果链表有环，那么两个指针必会相交，证明如下：
  

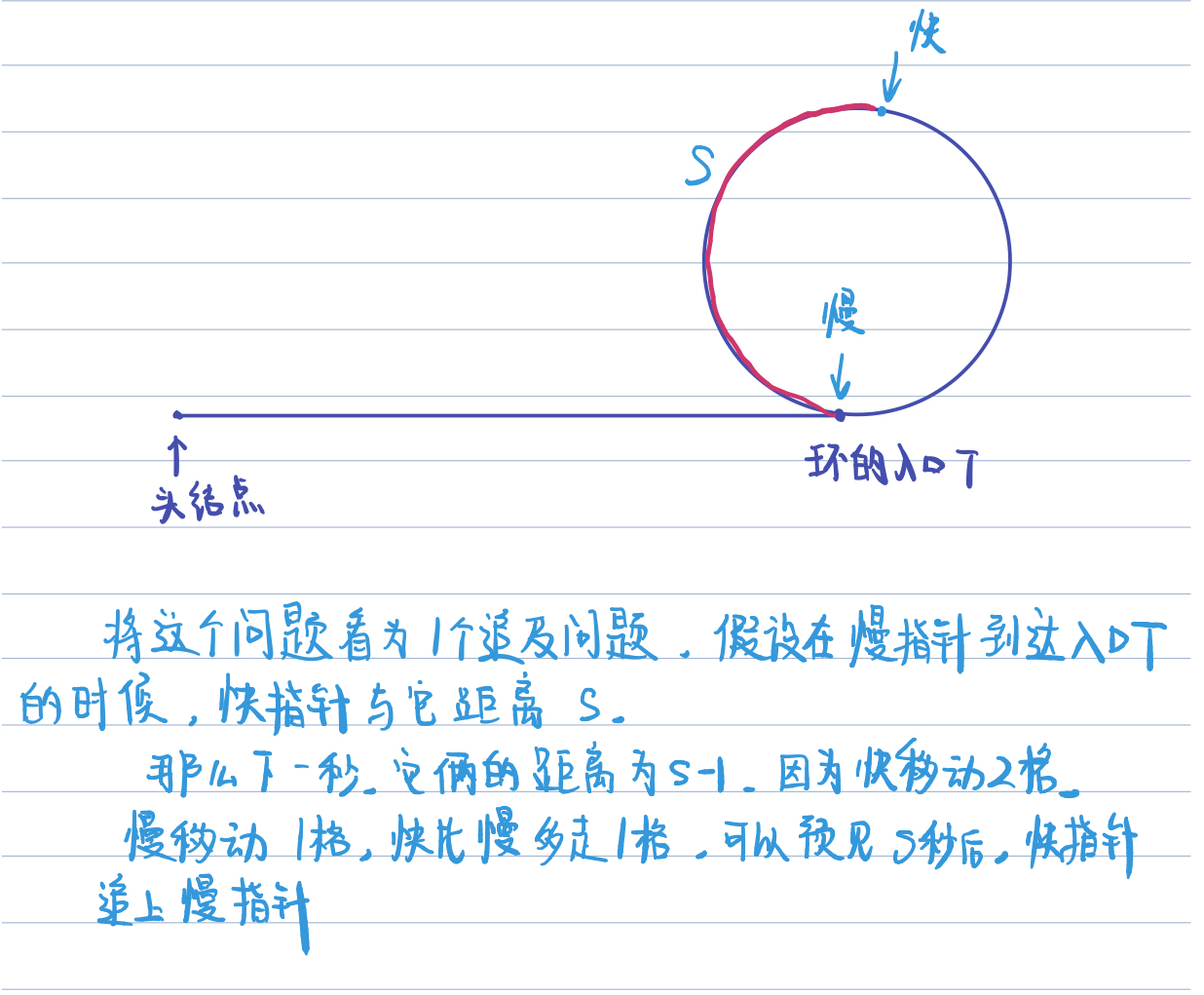
• 两指针相遇后，再将任意一个指针调至头节点，两个指针分别从各自的位置以每次一个节点的速度运行，直到再次相遇，相遇的那个点便为环的入口。证明如下：
  

 快慢指针的思想如上所述，给出的证明可能不怎么严谨，但应该还是能帮助理解的，具体的代码如下。

代码

#include <iostream>
#include <vector>
using namespace std;

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int backPos;
        // 设置快慢指针
        int fast = 0, slow = 0;
        while(true)
        {
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(fast == slow)
            {
                fast = 0;
                while(fast != slow)
                {
                    fast = nums[fast];
                    slow = nums[slow];
                }
                backPos = slow;
                break;
            }
        }
        return backPos;
    }
};

int main()
{
    Solution s;
    vector<int> nums = {1,3,4,2,5,3};
    cout << s.findDuplicate(nums) << endl;
    return 0;
}