2K Tallest Cow——差分

直接看代码

题目

(FJ)'s (N (1 ≤ N ≤ 10,000)) cows conveniently indexed (1..N) are standing in a line. Each cow has a positive integer height (which is a bit of secret). You are told only the height (H (1 ≤ H ≤ 1,000,000)) of the tallest cow along with the index (I) of that cow.

(FJ) has made a list of (R (0 ≤ R ≤ 10,000)) lines of the form "cow (17) sees cow (34)". This means that cow (34) is at least as tall as cow (17), and that every cow between (17) and (34) has a height that is strictly smaller than that of cow (17).

For each cow from (1..N), determine its maximum possible height, such that all of the information given is still correct. It is guaranteed that it is possible to satisfy all the constraints.

Input

Line (1): Four space-separated integers:$ N, I, H$ and (R)
Lines $2..R+$1: Two distinct space-separated integers (A) and (B (1 ≤ A, B ≤ N)), indicating that cow (A) can see cow (B).

Output

Lines (1..N): Line (i) contains the maximum possible height of cow (i).

Sample Input

9 3 5 5
1 3
5 3
4 3
3 7
9 8

Sample Output

5
4
5
3
4
4
5
5
5

题解

解题思路

最后让求每头牛最高是多少，先假定每头牛都是最高

每行输入两个数(x,y)表示在(x~y)中的没一头牛都比两边的小
那就把[x+1,y-1]的牛的高度消去(1)

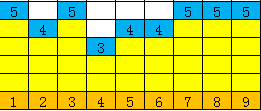
很容易写出代码

int main() {
    scanf("%d%d%d%d", &n, &h, &g, &m);
    for(int i = 1; i <= m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        if (x > y) swap(x, y);
        if (v[x][y]) continue;
        v[x][y] = 1;
        for(int j = x + 1; j < y; j++)
            a[j]--;
    }
    for(int i = 1; i <= n; i++)
        printf("%d
", a[i] + g);
    return 0;
}

这样写是(O(N^2))的时间复杂度，这道题1e4的数据还是能过的
数据大了就不行了，这里是对区间进行修改，可以用查分进行优化
需要注意的是，可能会有重复的数据，这里我用了二维数组v
如果数据过大，就使用map进行判重，
如果不清楚可以看我上一篇题解，有用到这个技巧

代码

#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e4+5;
int n, m, g, h, a[N];
bool v[N][N];
int main() {
    scanf("%d%d%d%d", &n, &h, &g, &m);
    for(int i = 1; i <= m; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        if (x > y) swap(x, y);
        if (v[x][y]) continue;
        v[x][y] = 1;
        a[x+1]--,a[y]++;
    }
    for(int i = 1; i <= n; i++)
        a[i] += a[i-1], printf("%d
", a[i] + g);
    return 0;
}