引射线法:从目标点出发引一条射线,看这条射线和多边形所有边的交点数射线法
时间复杂度:O(n) 适用范围:任意多边形
个人认为是非常不错的算法(不需考虑精度误差和多边形点给出的顺序),可以作为第一选择。
算法思想:
以被测点Q为端点,向任意方向作射线(一般水平向右作射线),统计该射线与多边形的交点数。如果为奇数,Q在多边形内;如果为偶数,Q在多边形外。计数的时候会有一些特殊情况,如图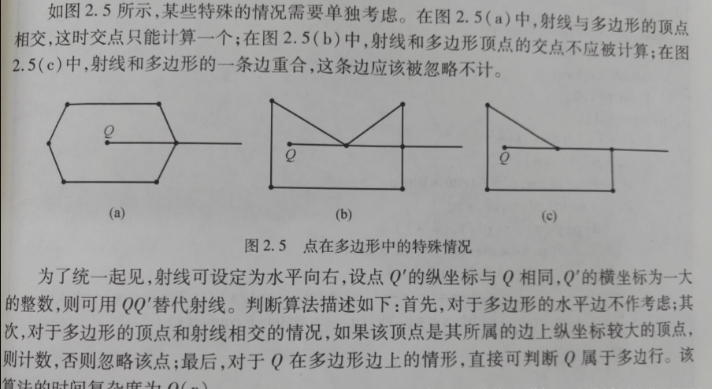
封装一个PointUtil里面用 boolean判断
/** * 判断一点是否在多边形内 * * @param target * @param points * @return */ public static boolean isPointInPolygon(LatLonPoint target, LatLonPoint[] points) { int iSum, iCount, iIndex; double dLon1 = 0, dLon2 = 0, dLat1 = 0, dLat2 = 0, dLon; if (points.length < 3) { return false; } iSum = 0; iCount = points.length; for (iIndex = 0; iIndex<iCount;iIndex++) { if (iIndex == iCount - 1) { dLon1 = points[iIndex].getLongitude(); dLat1 = points[iIndex].getLatitude(); dLon2 = points[0].getLongitude(); dLat2 = points[0].getLatitude(); } else { dLon1 = points[iIndex].getLongitude(); dLat1 = points[iIndex].getLatitude(); dLon2 = points[iIndex + 1].getLongitude(); dLat2 = points[iIndex + 1].getLatitude(); } double ALat = target.getLatitude(); double ALon = target.getLongitude(); // 以下语句判断A点是否在边的两端点的水平平行线之间,在则可能有交点,开始判断交点是否在左射线上 if (((ALat >= dLat1) && (ALat < dLat2)) || ((ALat >= dLat2) && (ALat < dLat1))) { if (Math.abs(dLat1 - dLat2) > 0) { //得到 A点向左射线与边的交点的x坐标: dLon = dLon1 - ((dLon1 - dLon2) * (dLat1 - ALat) ) / (dLat1 - dLat2); // 如果交点在A点左侧(说明是做射线与 边的交点),则射线与边的全部交点数加一: if (dLon < ALon) { iSum++; } } } } return (iSum % 2) != 0; }