说明:
KMeans 聚类中的超参数是 K,需要我们指定。K 值一方面可以结合具体业务来确定,另一方面可以通过肘方法来估计。K 参数的最优解是以成本函数最小化为目标,成本函数为各个类畸变程度之和,每个类的畸变程度等于该类重心与其内部成员位置距离的平方和但是平均畸变程度会随着K的增大先减小后增大,所以可以求出最小的平均畸变程度。
1、示例
# 导入相关模块
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 创建仿真聚类数据集
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
distortions = []
Ks = range(1, 11)
# 为不同的超参数拟合模型
for k in Ks:
km = KMeans(n_clusters=k,
init='k-means++',
n_init=10,
max_iter=300,
n_jobs=-1,
random_state=0)
km.fit(X)
distortions.append(km.inertia_) # 保存不同超参数对应模型的聚类偏差
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.figure('百里希文', figfacecolor='lightyellow')
# 绘制不同超参 K 对应的离差平方和折线图
plt.plot(Ks, distortions,'bo-', mfc='r')
plt.xlabel('簇中心的个数 k')
plt.ylabel('离差平方和')
plt.title('用肘方法确定 kmeans 聚类中簇的最佳数量')
plt.show()
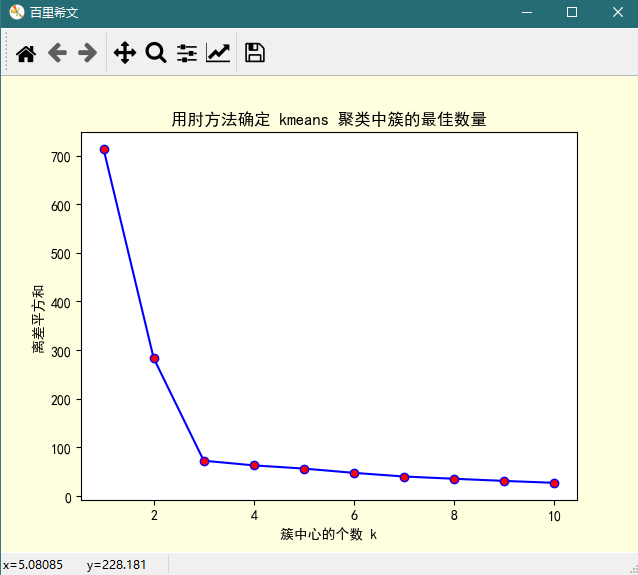
按语:
由上图可知,K 从 1 到 2, 从 2 到 3 的过程中,离差平方和减少的都相当明显,而 K 从 3 到 4,乃至 4 以后,离差平方和减少的都很有限,所以最佳的 K 值应该为 3(与仿真数据集的参数对对应)。由于上图看上去很像一只手肘,理论上最佳的 K 值在肘处取得,故而得名。
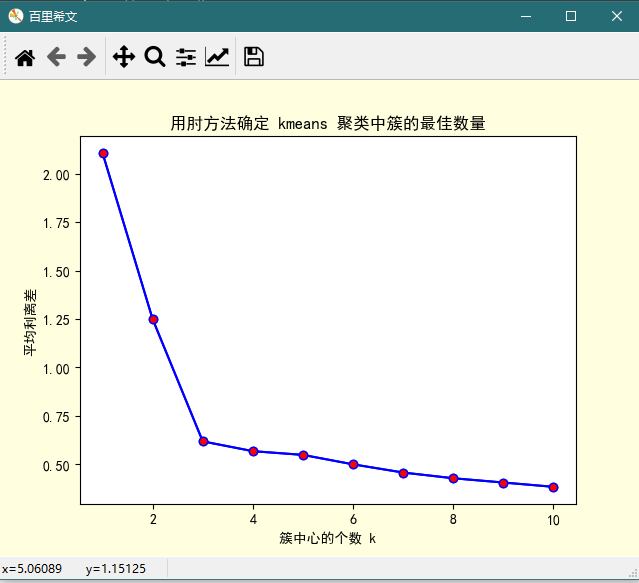
2、用平均离差效果似乎更明显
# 导入相关模块
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
# 创建仿真聚类数据集
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
meanDispersions = []
Ks = range(1, 11)
# 为不同的超参数拟合模型
for k in Ks:
km = KMeans(n_clusters=k,
init='k-means++',
n_init=10,
max_iter=300,
n_jobs=-1,
random_state=0)
km.fit(X)
meanDispersions.append(sum(
np.min(cdist(X, km.cluster_centers_, 'euclidean'), axis=1))/X.shape[0]) # 保存不同超参数对应模型的聚类偏差
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.figure('百里希文', facecolor='lightyellow')
# 绘制不同超参 K 对应的离差平方和折线图
plt.plot(Ks, meanDispersions,'bo-', mfc='r')
plt.xlabel('簇中心的个数 k')
plt.ylabel('平均离差')
plt.title('用肘方法确定 kmeans 聚类中簇的最佳数量')
plt.show()
图形: