一、动态数组
1、知道动态插入、动态删除,还有动态扩容
▪ 插入:

public void add(int index, int element) {
//对传入值进行判断是否合理,如果不合理时
//注意插入和删除、获取不同的是,可操作范围是 size (符合数组的特点,连续的内存的空间)
rangeCheckForAdd(index);
//确保容量充足
ensureCapacity(size + 1);
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//添加
for(int i = size; i > index; i--){
elements[i] = elements[i - 1];
}
elements[index] = element;
size++;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
}
▪ 删除:
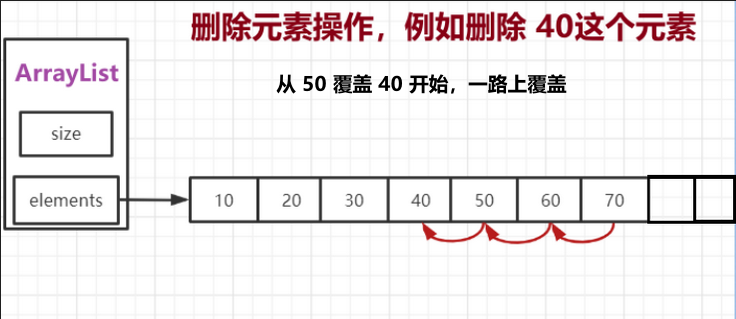
public int remove(int index) {
//对传入值进行判断是否合理,如果不合理时
rangeCheck(index);
int old = elements[index];
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//删除
for(int i = index + 1; i < size; i++){
elements[i - 1] = elements[i];
}
size--;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
//缩容操作
trim();
return old;
}
▪ 扩容:
/**
*动态数组的原理【通过再定义一个大点的新容量数组,然后原数组的元素复制到新数组中,从而实现扩容】
*/
private void ensureCapacity(int capacity) {
int oldCapacity = elements.length;
if(oldCapacity >= capacity) return;
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//新数组的容量【*1.5 通过移位运算提高性能】
int newCapacity = oldCapacity + (oldCapacity >> 1);
int[] newElements = new int[newCapacity];
//将原数组的元素复制到新数组
for(int i = 0; i < size; i++) {
newElements[i] = elements[i];
}
elements = newElements;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
System.out.println(oldCapacity + "扩容为:" + newCapacity);
}
二、单向链表
1、需要知道一般链表没有特点指出是什么链表都默认是单向链表
双向链表—> jdk 8 的LinkedList
知道动态插入、动态删除、还有查找某个位置index的结点(头指针从0开始移动index步)
单向链表的动态插入、动态删除 都是需要先找到
当前结点的前一个结点(index-1结点)
- 理由:因为单向,想要使用到前一个结点,没法直接通过"指针"拿到
▪ 查找某个位置index的结点(头指针从0开始移动index步)
/**
* 获取index位置对应的节点对象
*/
private Node<E> node(int index) {
rangeCheck(index);
Node<E> node = first;
for (int i = 0; i < index; i++) {
node = node.next;
}
return node;
}
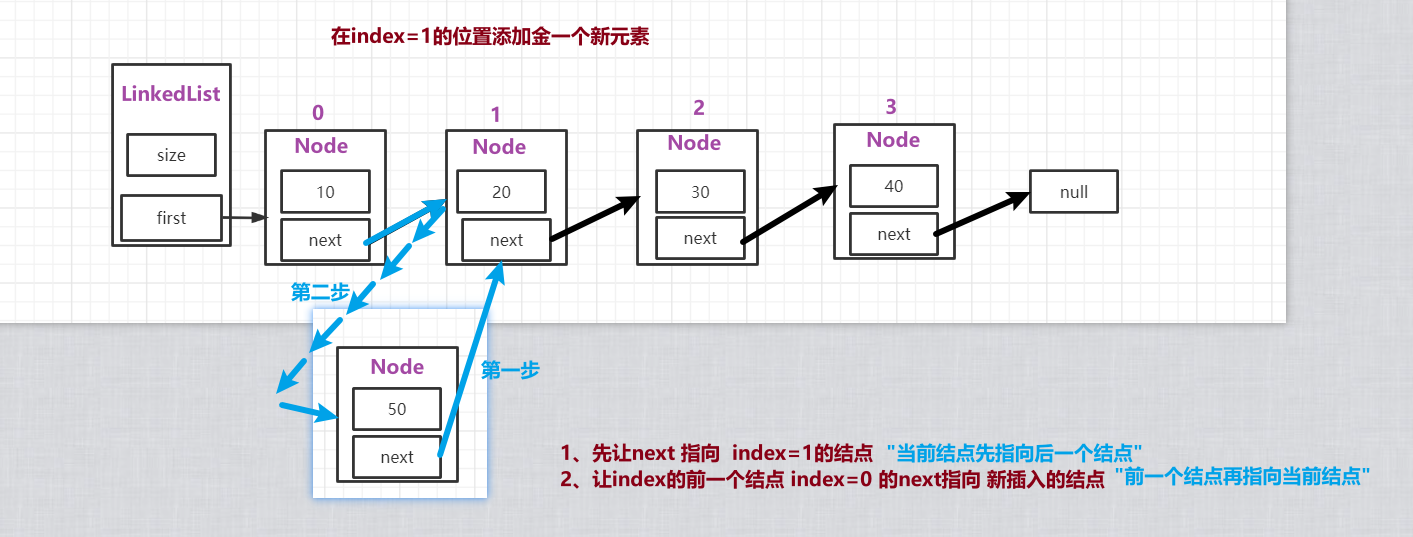
▪ 链表添加:
public void add(int index, E element) {
rangeCheckForAdd(index);
//添加【头指针情况--要分类,分是否插入到第一个位置】:
if (index == 0) {
first = new Node<>(element, first);
} else {//其他位置:先找到插入结点的前一个结点prev
Node<E> prev = node(index - 1);
//当前结点的next先指向prev的后一个结点,然后prev的next再指向当前结点
prev.next = new Node<>(element, prev.next);
}
size++;
}
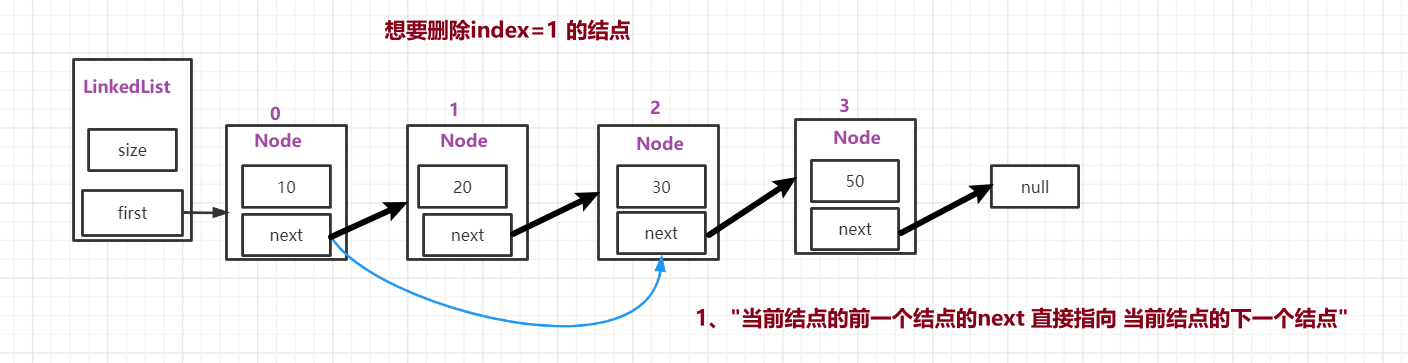
▪ 链表删除:
public E remove(int index) {
rangeCheck(index);
Node<E> node = first;
if (index == 0) {
first = first.next;
} else {
Node<E> prev = node(index - 1);
node = prev.next;
prev.next = node.next;
}
size--;
return node.element;
}
三、栈
◼ 栈是一种特殊的线性表, 只能在一端(栈顶)进行操作,先进后出原则
1、知道入栈 push,出栈 pop
只能在栈顶添加进元素,删除掉元素
四、队列
◼ 队列是一种特殊的线性表, 只能在头尾两端进行操作 , 先进先出原则
1、知道入队、出队
入队(插入元素):只能从队尾入队; 出队(删除元素):只能从队头出队
2、知道 双端队列
只能在头尾两端添加、删除的队列 ,头可以删除、插入元素,尾也可以删除、插入元素
五、二叉树
1、知道树的基本概念
- 节点概念:根节点、父节点、子节点、兄弟节点、叶子节点、非叶子节点
- 树概念:子树、左子树、右子树
- 度:子树的个数
- 层数
- 深度:从根节点到当前节点的唯一路径上的节点总数
- 高度:从当前节点到最远叶子节点的路径上的节点总数
2、知道二叉树的特点
-
每个节点的度最大为 2(最多拥有 2 棵子树)
-
左子树和右子树是有顺序的
-
即使某节点只有一棵子树,也要区分左右子树
3、根据节点访问顺序的不同,二叉树的常见遍历方式有4种
- 前序遍历:根节点、前序遍历左子树、前序遍历右子树
- 中序遍历:中序遍历左子树、根节点、中序遍历右子树
- 后序遍历:后序遍历左子树、后序遍历右子树、根节点
- 层序遍历:从上到下、从左到右依次访问每一个节点
▪ 递归实现前序、中序遍历、后序遍历
// 递归实现
ArrayList<Integer> nums = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) return nums;
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//拿到当前结点
nums.add(root.val);
preorderTraversal(root.left);//前序遍历左子树
preorderTraversal(root.right);//前序遍历右子树
return nums;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
}
- 中序和后序递归实现上思路相同,只不过是更改一下方法调用的顺序
▪ 非递归实现前序、中序遍历、后序遍历---使用栈 “先进后出”
/* 前序 */
public List<Integer> preorderTraversal1(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
//遍历过的点,不要了可以pop()掉,不断的pop(),然后才能拿到当前结点的右结点(先是不断的更新结点为左结点)
//然后没有左结点了,开始pop() 一层(一个结点)
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//先存储好所有的左子树
while (node != null) {
res.add(node.val);//已经拿到当前结点了
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
------------------------------------------------------- 核心代码结束 --------------------------------------------------
}
return res;
}
/* 中序 */
public List<Integer> inorderTraversal2(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null)
return res;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode node = root;
while(node != null || !stack.isEmpty() ) {
------------------------------------------------------- 核心代码开始 -------------------------------------------------
//先存储好所有的左子树
while(node != null) {
stack.push(node);
node = node.left;
}
node = stack.pop();
res.add(node.val);//已经拿到当前结点了
//切换到右子树
node = node.right;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
}
return res;
}
/* 后序 */
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if(root == null) return res;
Deque<TreeNode> stack = new LinkedList<>();
TreeNode prev = null;
while(!stack.isEmpty() || root != null) {
------------------------------------------------------- 核心代码开始 -------------------------------------------------
while(root != null) {
//先存储好所有的左子树
stack.push(root);
root = root.left;
}
root = stack.pop();
//右结点不存在,或者右结点是前一个遍历过的结点prev
if (root.right == null || root.right == prev) {
res.add(root.val);
prev = root;
root = null;//不加:超出内存
} else {//右结点存在
stack.push(root);
root = root.right;
}
------------------------------------------------------- 核心代码结束 -------------------------------------------------
}
return res;
}
前中后:都是先使用栈存储好左子树,然后因为前序、中序的遍历顺序:【前序:根 左子树 右子树; 中序:左子树 根 右子树】
- 刚好是使用栈先存储好左子树,再加上到下一层(当前结点【
既是"根",又是左】----当前结点上有老下有小哈哈哈)
❀ 为啥遍历是不断沿着左子树爬下下一层~~~为了实现拿到当前层的第一个结点。
❀ 对于树的遍历,到下一层,在形式上是先到了“根”(父结点)上。
▪ 迭代实现层序遍历---使用队列 “先进先出”
- 层序遍历作用:可以计算树的高度
- 判断一棵树是否为完全二叉树
public List<List<Integer>> levelOrder(TreeNode root) {
// 此题需要将同一层的结点放到一个数组中去(因此需要有个状态变量记录已经到达当前层的最后)
List<Integer> item = new ArrayList<>();
List<List<Integer>> result = new ArrayList<List<Integer>>();
if (root == null)
return result;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int levelSize = 1;// 当前层的结点数量
while (!queue.isEmpty()) {
// 拿到当前结点
TreeNode node = queue.poll();
levelSize--;
item.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (levelSize == 0) { // 当前层的结束,需要进入下一层
result.add(item);
item = new ArrayList<>();
// 进入下一层(观察发现,下一层的结点数量就是队列长度)
levelSize = queue.size();
}
}
return result;
}
六、二叉搜索树 Binary Search Tree(BST)
1、又称为:二叉查找树、二叉排序树
特点:任意一个节点的值都 大于其左子树 所有节点的值,任意一个节点的值都 小于其右子树 所有节点的值
- 它的左右子树也是一棵二叉搜索树
七、平衡二叉搜索树 Balanced Binary Search Tree(BBST)
1、平衡:当节点数量固定时,左右子树的高度越接近,这棵二叉树就越平衡(高度越低)
- 平衡因子:某结点的左右子树的高度差
2、经典常见的平衡二叉搜索树有:AVL树、红黑树
- 红黑树:Java 的 TreeMap、TreeSet、HashMap、HashSet
八、AVL 树
1、理解各种旋转:
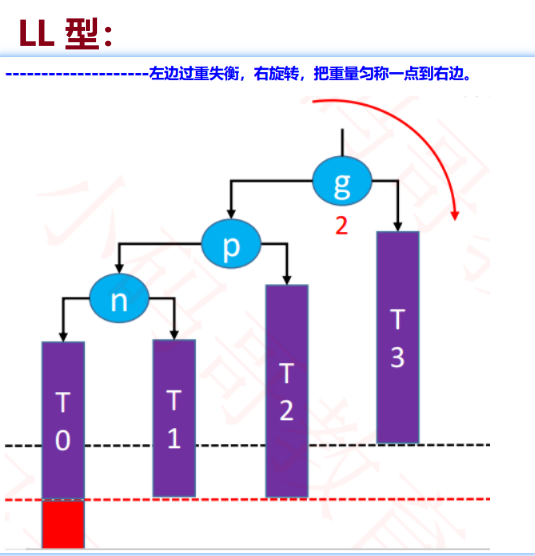
- LL:
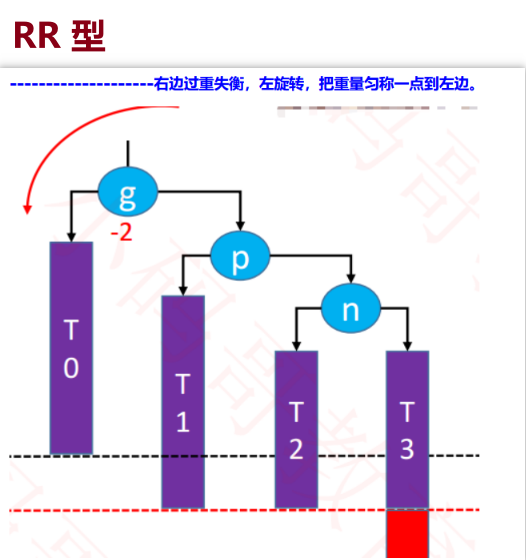
- RR:
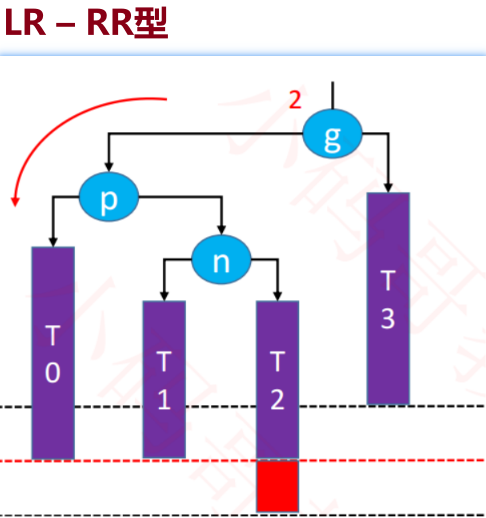
- LR-RR:
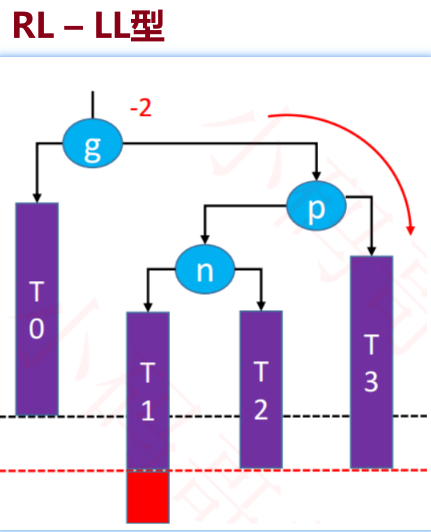
- RL-LL:
2、旋转的意义:就是为了匀称掉失衡的状态
✿ 最后一个字母就是提示失衡的情况
● LL:是左边失衡~右旋转
● RR:是右边失衡~左旋转
● LR-RR: 看到该结构最后一对是 RR,是右边失衡~左旋转,处理后得到-LL 是左边失衡~右旋转
● RL-LL: 看到该结构最后一对是 LL,是左边失衡~右旋转,处理后得到-RR 是右边失衡~左旋转
▪ 旋转代码
- LL型【右旋转】的代码:
g.left = p.right;
p.right = g;
形态理解上: 【g的左边太重了】
g.left = p.right; ● 代码意思:(g的左边减轻重量)p 丢掉孩子,丢给了离开g最近的一个孩子(右孩子),即g拿到p的右孩子
p.right = g; ● 代码意思:p丢掉孩子,g领养完孩子,p变轻了爬升了,g变重下沉了,于是p和g构建新的关系:p的右孩子变成了下层的g。
形象生动地使用现实中天平平衡的理解角度即可啦~
- 其他旋转同理
九、B树
1、了解添加发生上溢、删除发生下溢
- 上溢解决:元素上升与父元素合并 下溢解决:元素下沉和子元素合并
2、m 阶B树(最多可以有m个子节点):
-
节点存储元素个数:设为x
- 根节点:1 ≤ x ≤ m − 1; 非根节点:┌ m/2 ┐ − 1 ≤ x ≤ m − 1
- 重点了解的是 4 阶B树:存储的元素个数,根节点或非根节点都是: 1 ≤ x ≤ m − 1
-
如果有子节点,子节点个数是存储的元素个数加一: m = x + 1
十、红黑树(Red Black Tree)
1、红黑树也是一种自平衡的二叉搜索树
- 以前也叫做平衡二叉B树
2、红黑树必须满足以下 5 条性质
① 节点是 RED 或者 BLACK
② 根节点是 BLACK
③ 叶子节点(外部节点,空节点)都是 BLACK
④ RED 节点的子节点都是 BLACK
- RED 节点的 parent 都是 BLACK
- 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点
⑤ 从任一节点到叶子节点的所有路径都包含相同数目的 BLACK 节点
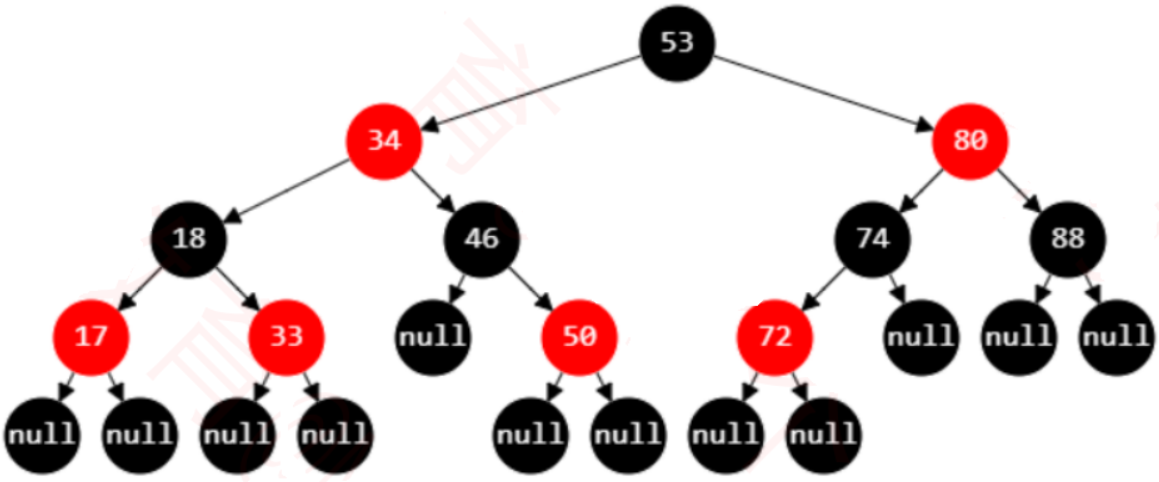
3、红黑树 和 4阶B树(2-3-4树)具有等价性
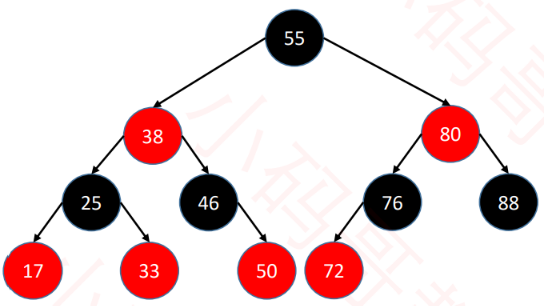
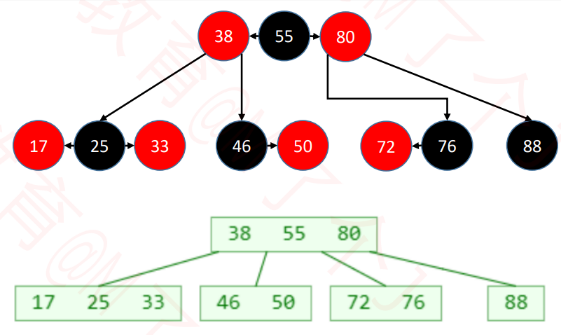
-
BLACK 节点与它的 RED 子节点融合在一起,形成1个B树节点
-
红黑树的 BLACK 节点个数 与 4阶B树的节点总个数 相等
4、AVL树 vs 红黑树
-
复杂度:avl树和红黑树一样,搜索、添加、删除 都是 O(logn),旋转调整次数两者不同。avl树:添加仅需 O(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整;红黑树:添加、删除都仅需 O(1) 次旋转调整
-
搜索次数多的选avl树
-
和avl树比较, 红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树
-
红黑树的平均统计性能优于AVL树,实际应用中更多选择使用红黑树
5、红黑树的增加元素、删除元素
◼ 建议新添加的节点默认为 RED,这样能够让红黑树的性质尽快满足(性质 1、2、3、5 都满足,性质 4 不一定)
▪ 红黑树增加元素
▪ 红黑树删除元素
十一、二叉堆、优先级队列
1、大根堆:任意节点的值总是 ≥ 子节点的值
- 也叫最大堆、大顶堆
- 小根堆:任意节点的值总是 ≤ 子节点的值
2、大根堆的应用:优先级队列的实现底层就是大根堆
▪ 大根堆 添加元素:
- 上滤:向上调整
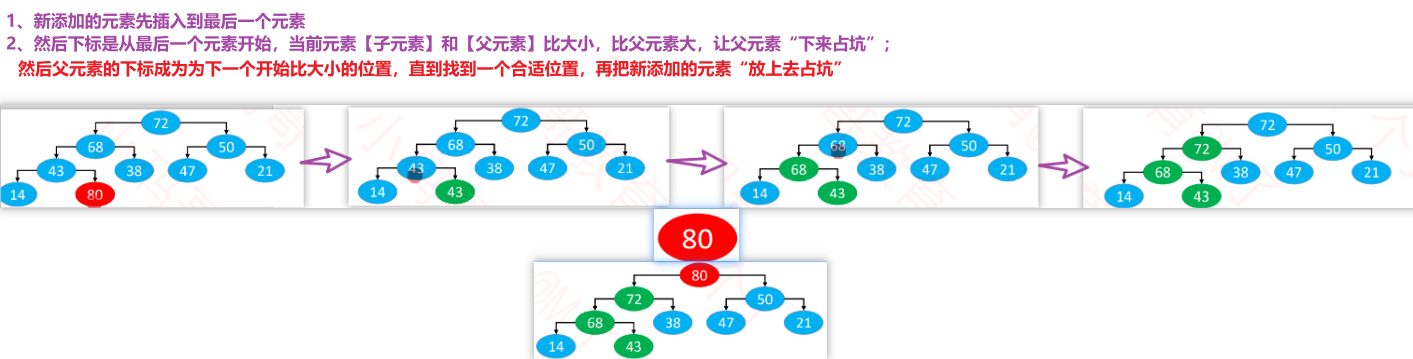
public void add(E element) {
//检查元素是否具有可比较性【排除null】
elementNotFoundCheck(element);
// 扩容检查、扩容操作
ensureCapacity(size + 1);
//按数组添加特点【每次都是添加到最后的位置,添加完数组长度++】
elements[size++] = element;
//维持二叉堆的特点【大根堆特点】~ 上滤
siftUp(size -1);
}
/**
* 上滤
*/
private void siftUp(int index) {
// 插入element 随着比较不断的上移【选择一个合适的位置(插入的当前结点比父结点小)】,而是最终确定位置后,放一下]
E element = elements[index];
------------------------------------------------------- 核心代码开始 -------------------------------------------------
while (index > 0) {
int parentIndex = (index - 1) >> 1;
E parent = elements[parentIndex];
if (compare(element, parent) <= 0) break;
//让比较小的父元素放到子元素位置
elements[index] = parent;
// 重新赋值index
index = parentIndex;
------------------------------------------------------- 核心代码结束 -------------------------------------------------
}
elements[index] = element;//找到最终的位置index
}
▪ 大根堆 删除元素:
- 下滤:向下调整

public E remove() {
emptyCheck();//检查数组是否为空
E root = elements[0];
int lastIndex = --size;
elements[0] = elements[lastIndex];
elements[lastIndex] = null;
//下滤
siftDown(0); //根据索引进行下滤操作
return root;
}
/**
* 下滤
*/
private void siftDown(int index) {
int half = size >> 1;
E element = elements[index];
while(index < half) {//index 必须是非叶子节点
// 默认拿是左边跟父节点比大小
int childIndex = (index << 1) + 1;
E childElement = elements[childIndex];
int rightIndex = childIndex + 1;
if(rightIndex < size
&& compare(elements[rightIndex], childElement) > 0) {
childElement = elements[childIndex = rightIndex];
}
if(compare(element, childElement) >= 0) break;
//子结点大的话
elements[index] = childElement;
index = childIndex;
}
elements[index] = element;
}
3、原地建堆
-
自上而下的上滤:即从第一个元素开始到最后一个元素,采用的都是先放到最后一个位置,然后上滤(向上调整) 【时间复杂度是 O(nlogn)】
for(int i = 1; i < size; i++){ siftUp(i); } -
自下而上的下滤: 从底部的非叶子结点开始到第一个元素,采用的都是先和堆顶交换,然后下滤(向下调整) 【效率更高,时间复杂度是 O(n)】
for(int i = (size >> 1) -1; i >= 0; i--){ siftDown(i); }
如果本文对你有帮助的话记得给一乐点个赞哦,感谢!