八大排序算法之直接插入排序(教你用生活的想象,读懂直接插入算法)
1,生活小游戏:"算法来源于生活",哈哈哈,还记得玩过的抽牌小游戏吗,你从放在地上的那一堆未知的牌【无序】抽一张牌后,
小脑袋机灵的将抽到的牌放到手中牌【早已被你打理得仅仅有序啦】的某个合适位置后【手中牌保持井井有序】。
手中牌【有序】<-------------------------------- 地上牌【无序】
直接插入排序 == “将牌一张张从地上抽起,然后在手中打理得井井有序”。
2,图解:

从图解可以知道咱需要“插入”,而本题咱用的存储空间是数组~则涉及到了数组的空间移动问题了
~数组移动是从最后一个元素开始,前一个元素的值赋值给后一个元素。
3,简单分析一下过程:一开始,在整体牌中,有序区的牌只有一张,放在第一个位置,无序区的牌就是从第二张到最后一张结束。
然后,咱不断的从无序区【从第二张牌开始直到最后一张牌~一个遍历过程】拿牌插入到有序区的合适位置
【需要通过取出来的牌与已经在有序区的牌比较大小才知道是否合适~也是一个遍历过程,从有序区的第一个位置开始直到
取出的牌 的前一个位置结束】。
4,所以:外循环(取出无序区的牌):从第二张牌开始到最后一张牌 【无序区的范围】
内循环(在有序区找合适位置将取出的牌插入):从第一张牌开始直到 取出的牌 的前一张牌 【有序区的范围】
5,假设,有序区是从小到大排序,则咱因为数组移动空间问题,【有序区的范围】从最后一个元素开始移动,
于是乎,也从最后该元素比较起,一旦找到在有序第一个数小于取出的数,则有序区的该数后边便是合适插入位置。
6,比较过程,形象生动用一个想象说明吧,看图解(咱有一个从小到大的赛道跟一个球),当球停止,便也找到合适位置了:
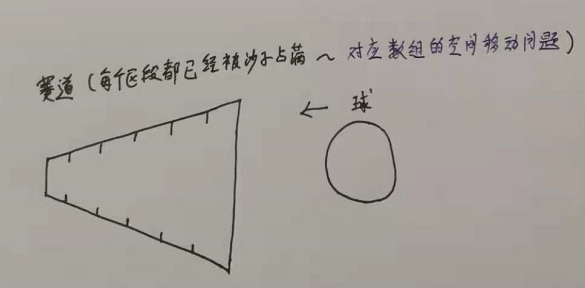
7,直接上代码,分析如上:
for(int i = 2; i <= N; i++){ //外循环,从无序区取出牌 arr[0] = arr[i]; //arr[0]是哨兵元素,后边再补充哨兵元素的好处 for(j = i - 1; arr[0] < arr[j]; j--){ //内循环,从有序区最后一个元素开始比较,知道“球”卡住了,便找到合适位置 arr[j + 1] = arr[j]; } arr[j + 1] = arr[0]; }
ps:代码优化:【主要是优化在有序区查找那个合适位置,原来咱是从最后一个元素开始比较麻,顺带一起移动元素空间,
优化一下:先找到合适位置,后边再移动空间~二分(折半)查找优化】
✿✿ 先讲清楚在这个有序区找到一个合适位置哈【有序(从小到大)】:
正向思维~咱是从有序区第一个数开始找起,找找找,遇到第一个比【哨兵(待插数)】大的数,
因为从小到大排序,咱知道从这个数开始的后边的数都会比(哨兵元素)大了,于是合适的位置就是这个数的前面;
逆向思维~咱是从有序区最后一个数开始找起,找找找,遇到第一个比【哨兵(待插数)】小的数,
因为从小到大排序,咱知道从这个数开始的前边的数都会比(哨兵元素)小了,于是合适的位置就是这个数的后面;
for(int i = 2; i <= N; i++){ //外循环,从无序区取出牌 arr[0] = arr[i]; //arr[0]是哨兵元素,后边再补充哨兵元素的好处 //二分查找,先在有序区找到那个合适位置先 int low = 1; int hight = i - 1; while(low <= height){ //不断缩小查找范围 int mid = (low + height)/2; if(arr[0] < arr[mid]){ height = mid - 1; }else{ low = mid + 1; } } //移动空间 for(int j = i - 1; j >= height + 1; j--){ //内循环,从有序区最后一个元素开始比较,知道“球”卡住了,便找到合适位置 arr[j + 1] = arr[j]; } arr[height + 1] = arr[0]; }
8,哨兵元素好处:参考《数据结构c语言版严蔚敏PPT.pdf ~
https://wenku.baidu.com/view/9e73cb8b69dc5022aaea00c1.html》
(1)不用额外增加辅助空间;
(2)省去对下标越界的判断;
