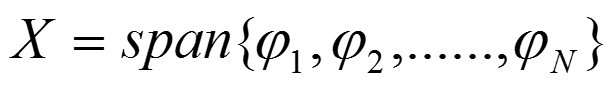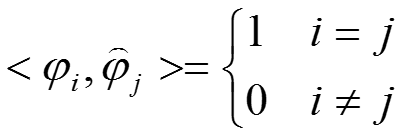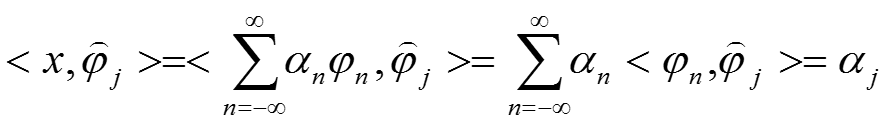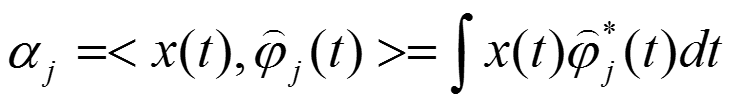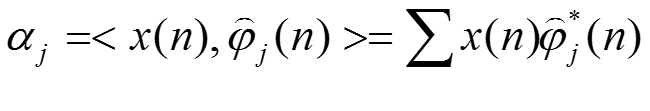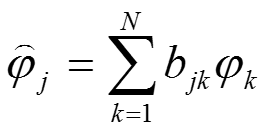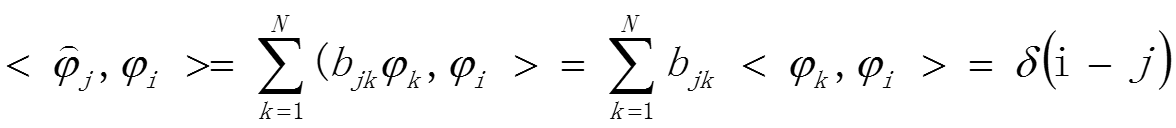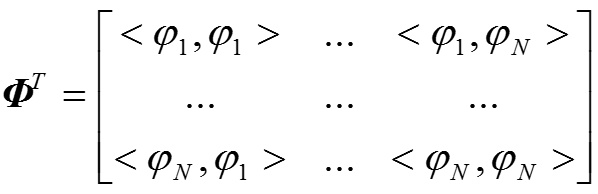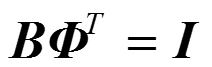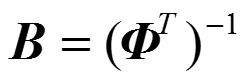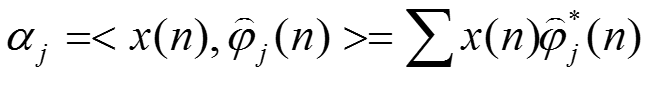设是X由一组向量
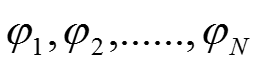
所张成,即:
如果
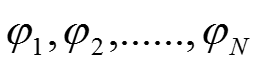
线性独立,我们则称它们为空间中的一组基”。
那么信号x可以离散表示如下:
若
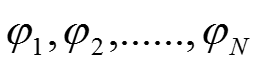
是一组两两互相正交的向量,展式称为x的正交展开。分解系数
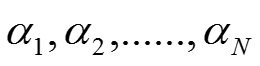
是在各个基向量上的投影。
设向量
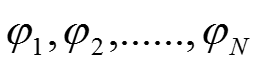
和向量
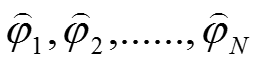
满足如下双正交关系:
那么,我们对原始信号就行投影变换(內积):
看看,我们把最关心的分解系数给弄出来了!现在的问题是与原始基双正交的向量怎么求?
1.1 信号分解、对偶基(倒数基)、正交基
关于信号的分解表示,我们可以从连续时间和离散时间分开分析:
对于连续时间信号:
对于离散时间信号:
以上两式称为信号的变换。“变换”的结果即是求出一组系数。
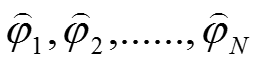
称为
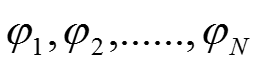
的“对偶基”,或“倒数基”。
双正交关系指的是两组基之间各对应向量之间具有正交性,但每一组向量之间并不一定具有正交关系。
N 维空间中的正交基:
如果一组基向量
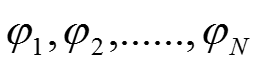
的对偶向量即是其自身,也那么这一组基向量构成了N 维空间中的正交基。
1.2 完备性/标架
若X空间中的任一元素x都可由一组向
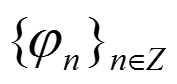
量作式 :
的分解,那么我们称这一组向量是“完备(complete)”的。
如果
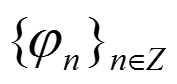
是完备的,且是线性相关的,那么,由
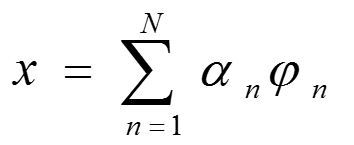
表示x必然会存在信息的冗余,并且其对偶向量将 不会是唯一的。这时,我们称
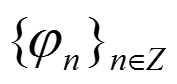
构成空间的一个“标架(frame)”。
若
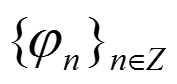
是完备的,且是线性无关的,则
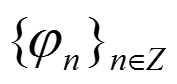
是X中的一组基向量,这时,存在且唯一,即存在
的双正交关系。则对偶及存在,且是唯一的。
对于正交关系,那么他的对偶基就是自己本身。
1.3 详细证明
将对偶基向量,用基向量表示:
将基向量与对偶基进行內积计算:
令:
这样,我们可以得到如下公式:
这样我们就可以通过基向量,求得他的对偶基向量。
2.1为什么信号分解系数线性相关情况下,对偶基不唯一?
基向量现象相关,导致B矩阵是奇异矩阵,那么得到的“对偶基向量”必定不唯一。
2.2为什么信号分解系数双正交情况下,对偶基唯一?
单位阵I,那么此时的B是固定的唯一的,就是基向量的逆。
2.3为什么信号分解系数正交情况下,对偶基就是本身?
正交情况下,矩阵的逆就是矩阵的转置,那么就是自己本身,如此简单的运算,也正是正交变换在硬件领域很受欢迎的原因。因为对矩阵求转置的复杂度要远远低于逆运算。
2.4分解系数可以通过对偶基向量和原始信号的內积求得,这有什么物理意义?
通过上面公式,我们可以通过物理角度进行思考。所谓的投影运算也可以看成是相似性衡量问题。如果对偶基向量与原始信号越相似,分解系数应该越大!
原文见:http://m.blog.csdn.net/shenziheng1/article/details/60610724
所张成,即:
如果线性独立,我们则称它们为空间中的一组基”。
是一组两两互相正交的向量,展式称为x的正交展开。分解系数
是在各个基向量上的投影。
设向量和向量
满足如下双正交关系:
那么,我们对原始信号就行投影变换(內积):看看,我们把最关心的分解系数给弄出来了!现在的问题是与原始基双正交的向量怎么求?称为
的“对偶基”,或“倒数基”。
双正交关系指的是两组基之间各对应向量之间具有正交性,但每一组向量之间并不一定具有正交关系。N 维空间中的正交基:如果一组基向量的对偶向量即是其自身,也那么这一组基向量构成了N 维空间中的正交基。
量作式 :
的分解,那么我们称这一组向量是“完备(complete)”的。如果是完备的,且是线性相关的,那么,由
表示x必然会存在信息的冗余,并且其对偶向量将 不会是唯一的。这时,我们称
构成空间的一个“标架(frame)”。
若是完备的,且是线性无关的,则
是X中的一组基向量,这时,存在且唯一,即存在
的双正交关系。则对偶及存在,且是唯一的。对于正交关系,那么他的对偶基就是自己本身。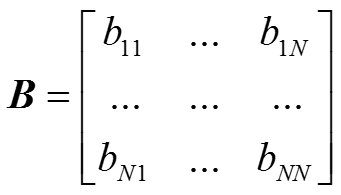 这样,我们可以得到如下公式:这样我们就可以通过基向量,求得他的对偶基向量。
这样,我们可以得到如下公式:这样我们就可以通过基向量,求得他的对偶基向量。