python常用序列list、tuples及矩阵库numpy的使用

近期开始学习python机器学习的相关知识，为了使后续学习中避免编程遇到的基础问题，对python数组以及矩阵库numpy的使用进行总结，以此来加深和巩固自己以前所学的知识。

Section One：Python数组的使用

在python中，数组这个概念其实已经被淡化了，取之的是元组和列表，下面就列表和元组进行相关的总结和使用。

　　Subsection One: List

　　list列表本质是一种序列类型的数据结构，有点类似于C/C++中所学的数组，但又不同。他们的相同之处在于，二者中的每个元素都分配有一个索引值来进行访问，如：

#python list
list1 = ['physics', 'chemistry', 1997, 2000]
print(list1[0])

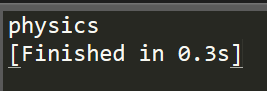
而在C/C++中我们知道，数组也可以通过这种数组名加索引值的方式来访问，在此不做赘述。

但是，细心的话，我们会发现，python中的列表与C/C++中有所不同，它可以包含不同的数据类型，而C/C++中则不可以。此外，在上面的代码中，我们可以看到，二者有着相同的创建方式。

但在python中，对于list列表类型的访问，有着不同的方式，下面就列表的访问进行总结：

"""List:
--------------------------------
"""
# create a list
list1 = ['physics', 'chemistry', 1997, 2000]

# two methods to access a list as follows:
print "list1[0]", list1[0] 
print "list1[1:4]", list1[1:4]

print "list1[-1]", list1[-1]
print "list1[-2]", list1[-2]

print "list1[1:]", list1[1:]

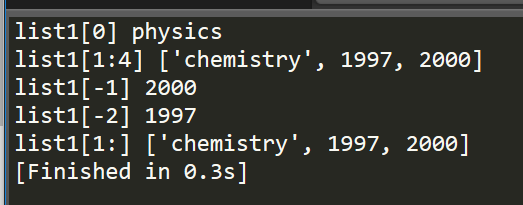
从上面两种方式，其实可以看到，python中的列表可以通过"起始索引：终止索引（可选）"的方式，来直接访问列表中的一串数据，这在C/C++中是无法做到的，这给我们带来极大的便利性，加上终止索引，表示访问从起始索引到终止索引之间的全部数据，不加则意味着要访问从起始索引到该列表末尾的全部数据。

此外，在列表中，索引值为负代表着从列表末尾来访问这个列表，图上图三、四例子可以看到。

此外，python中对于列表，引入了以下几种方法来更新和删除列表，并赋予几种访问列表属性的方法。

# update and delete 
list1.append('Google')
print list1

列表可以通过append方法，往列表的末尾添加新的元素，在list1列表的基础上，这里添加了一个叫做google的字符串元素。

del list1[2]
print "after deleting value at index 2", list1

可以看到，使用del函数将索引为2的数据删除了，此外，del函数还能结合之前提到的访问数组的方式来删除相关元素，如：

del list1[1:]
print "after deleting value by list1[1:]", list1

同理，采用起始index：终止index的方式，也是能够实现删除列表中一段数据的。

此外，python中提供了一个len函数，来获取一个列表的长度，使用"+"操作符能够实现不同数组之间的合并，使用"*"操作符实现创建包含n个相同元素的列表，以及一些循环和遍历方式来确定数据是否在列表中，下面给出相关的操作：

"""List:
--------------------------------
"""
# create a list
list1 = ['physics', 'chemistry', 1997, 2000]
list2 = [1, 2, 3 , 4]

l = len(list1)
print "access len function to get the length of list1"
print l

# + operator
print list1 + list2

list3 = list1 + list2

print "list3:", list3

# * operator
list4 = ['hhhh'] * 4
print list4

#traverse
print "traverse list1:"
for x in list1:
    print x

#confirm x in list
print "confirm x in list"
print 2 in list1
print 1997 in list1

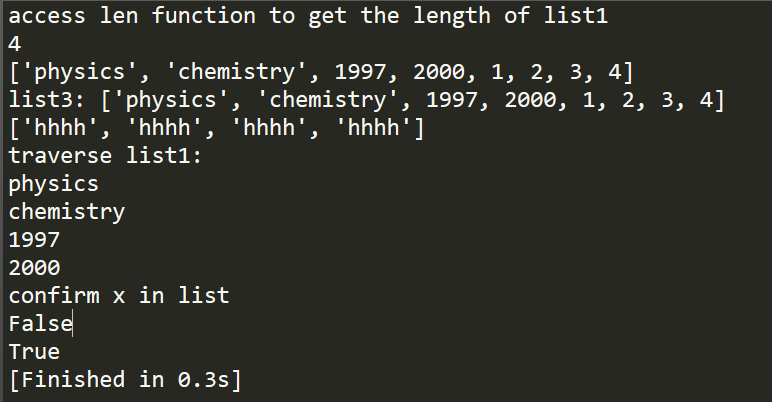
此外，还可以通过min和max函数来获取列表的最大最小值，count函数用以计算某元素在列表中的出现次数，remove来移除匹配到的数据，sort函数进行排序，reverse函数进行逆序，这些可以在list的官方文档中查询到。

　　Subsection Two: 元组

　　元组的创建根列表的很类似，但是它用括号进行创建：

"""
Tuples
------------------------------
"""

tup1 = (1, 2, 3, "Google")
print tup1

tup2 = ('flesh',)
print tup2

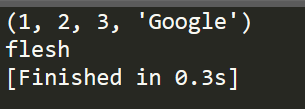
细心的小伙伴们可能会看到，我在创建第二个tuples的时候，里面虽然只有一个元素，但是，我还是用了一个逗号，其实，这是很有必要的，虽然不加也不会有编译错误，在这部分代码中。但是，在其他情况则不一定了，比如，我们使用元组作为返回参数，如果不加逗号，但是返回的元组中只有一个数据，比如26，那么，计算机就会因为无法识别该元素是数字26还是元组26。因此，加上是必要的，也有助于我们养成良好的编程习惯。

元组的访问呢与列表是一样的，因为它们俩都是python中最为常见的序列结构，在这里不做赘述，有兴趣的小伙伴可以自己去尝试一下下，值得注意的是，访问时的形式与列表的相同，不是L(index)的方式，而是L[index]。

此外，在元组中，对相关数据的修改是非法的，如下所示：

print "modify the data at index 2"
tup1[2] = 100
print tup1

所以给位小伙伴们在使用元组时一定要注意呀！

但是元组中，可以使用"+"以及"*"两个操作符来进行对元组的修改。

其余的相关方法如len等，而这类似，可以通过查阅文档来了解。

Section Two: Numpy库的使用（后续补充，要吃饭了23333）

补充：

Numpy是python中的矩阵库，可以方便的让我们学习。

可以使用cmd命令行来安装该库，命令如下：

pip install Numpy

安装完成后，即可使用。python提供了一个pydoc命令，可以用于查看本地所安装的python库，也是在cmd命令行中输入。

python -m pydoc -p 1234

-p指定启动的服务的端口号，可以随意指定不冲突的端口号

-m则是py中的一种工作模式了

1234就是-p下指定的一个端口号。运行后cmd会出现这样的结果：

然后根据所给的url直接在浏览器中输入，就可以访问到本地的库文档，个人比较喜欢直接查文档的方式进行学习。

该界面中包含numpy库下辖的多个类以及各个类中所包含的函数模块，并在每个接口部分，给出了相应的使用案例。

下面给出numpy的使用：

numpy的调用，与其他库文件的调用一样，采用import方式进行调用：

import numpy as np

通过这种方式，可以将本地的numpy库，导入当前的py文件中进行使用。此外，numpy给python的学习者以极大的便利来使用矩阵，尤其是其所提供的help函数，能够在使用者不知道或者忘记怎么使用其内部函数的时候，给予帮助。

调用方式如下：

help（function name）

在这里我以下面这个例子为例：

"""
Numpy Learning
------------------------------------------------------
"""

import numpy as np

help(np.sort)

sort函数是numpy中自带的一个排序函数，当运行help方法进行获取他的使用后，就可以在console框中得到相应的调用案例：

这种方式能够在一定程度上提高我们查询文档的速度。

对于矩阵的使用，可以自行生成，也可以借助numpy中所带的相关类进行获取，如Datasource，该类可以通过如下方式导入进行使用

from numpy import DataSource

导入后，就可以直接进行调用，以鸢尾花数据库中的数据为例：

实例化DataSource对象以后，该对象包含相对应的方法，可以在上文中提到的本地库函数界面中查询到，典型的就有exists方法，用以判断访问的数据是否存在。

"""
Numpy Learning
------------------------------------------------------
"""

import numpy as np
from numpy import DataSource

# method to get data
url_name = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
repos = DataSource()
print repos.exists(url_name)

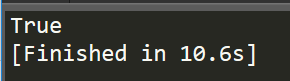
运行后输出为True，说明存在，我们可以直接通过url_name来访问相应的数据。

"""
Numpy Learning
------------------------------------------------------
"""

import numpy as np
from numpy import DataSource

# method to get data
# url name to access
url_name = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
ds = DataSource()
dataset = ds.open(url_name, mode='r')

for key in dataset:
    print key

数据的访问这里选择只读形式，然后通过for循环对获取的数据进行解析输出：

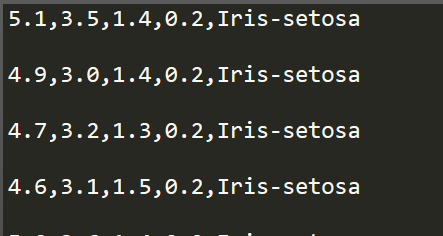
这种方式获取的数据存在一定的局限性，因为每个key其实是一个list对象，其中数据全部为字符串型数据。进一步的使用则需要对数据进行解析，可以简单的通过pandas数据库来获取整理数据，这个库是python中的一个数据分析库，事倍功半，pandas的使用，将会在后续另一篇blog中进行叙述。本文采用一些线性代数中的简单实例，来使用numpy矩阵库。

 ex1：求解下列线性方程：

通常，线性方程可以表示成Ax = b的形式，A即为线性方程组的系数矩阵，b即为右侧的值构成的列向量。则可以通过在方程两边同乘以系数矩阵的逆矩阵来求得x的解。在这里给出我手解得到的值x1=1;x2=x3=0。

下面借助numpy进行求解，代码如下：

#coding:utf-8
"""
Numpy Learning
------------------------------------------------------
"""

import numpy as np
import numpy.linalg as lg

# create an matrix
"""
np.array(parameter matrix)
the matrix can be one-dimensional or multi-dimensional
It's worth noting that if matrix is one-dimensional, the fellow method 
can be used:
    np.array([1,2,3,4])
else like the given sample
"""
# A = np.array([1, 2, 3, 4])
# print "onr-dimensional matrix: "
# print A
# A = np.array([1, 2, 3, 4])
A = np.array([[1, 2, 3], [2, 2, 5], [3, 5, 1]])
b = np.array([[1], [2], [3]])

A_inv = lg.inv(A)

# x = np.dot(A_inv, b)
x = A_inv.dot(b)
print "x is calculated by dot function:"
print x
# print "x is calculated by * operation: "
# print A_inv * b

print("The inverse of A is :")
print A_inv
print("Column vector b is :")
print b
print("The result of A_inv * b is :")
print A_inv * b

print "The examples of * operator :"
a = np.array([[1, 2, 3], [2, 2, 5], [3, 5, 1]])
b = np.array([[1], [2], [3]])
print a * b

# error
# a = np.array([[1, 2, 3], [2, 2, 5], [3, 5, 1]])
# b = np.array([[1], [2]])
# print a * b

# error
# a = np.array([[1, 2, 3], [2, 2, 5], [3, 5, 1]])
# b = np.array([[1, 2], [2, 2], [3, 2]])
# print a * b

代码中给出了使用numpy创建矩阵的两种方式，一种是创建多维矩阵另一种则是创建一维的矩阵，即行向量。可以看到，当创建行向量的时候，只需要传入一个list类型的对象即可，而创建多维矩阵的时候，需要以行向量作为一个list的元素构成一含有多个子list的一个list作为参数传递进去，以此来创建矩阵。

在这里用到了numpy底下linalg中的一个方法即inv方法，用于求矩阵的逆矩阵。需要注意的是，numpy中，对" * "、" / "、" - "、" + "进行了重载，以此来满足矩阵的运算需要，但是，在这些运算符中，" * "运算符不同于其他工具中的功能，它实现的不是矩阵的点乘，而是对矩阵的元素进行操作，即，当两个矩阵a、b的行相同，且当矩阵a或b的列满足矩阵a的列数等于矩阵b的列数，或者矩阵a或者b的列数等于1时，两个矩阵中的元素进行操作，上述代码的运行结果可以很直观的看到这一点。

上述代码的运行结果如下所示：

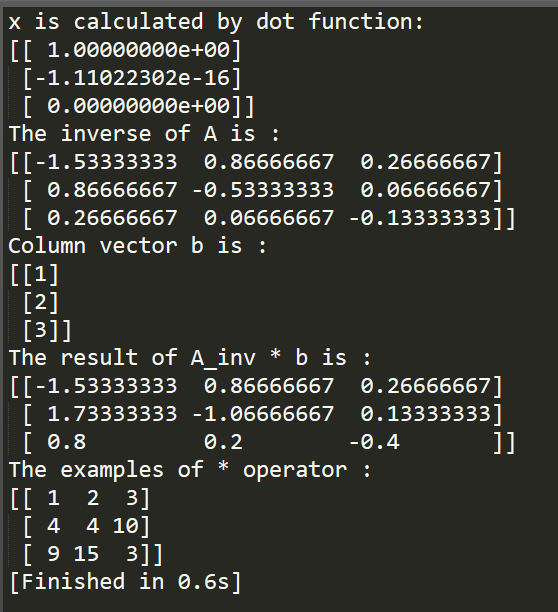
从上述代码可以看到，矩阵的点乘是每个numpy矩阵对象自带的方法，可以通过np.dot(parameter A, parameter B)的方式，也可以直接A.dot(B)。而求逆运算则包含在linalg模块中。

此外，在每个numpy对象中包含以下几种属性：ndim、shape、size、dtype、itemsize以及data，下面以ex1线性方程组的系数矩阵A为例来输出这些属性。

A = np.array([[1, 2, 3], [2, 2, 5], [3, 5, 1]])
print "The metrix A"
print A
print "A.ndim: "
print A.ndim
print "A.shape: "
print A.shape
print "A.size: "
print A.size
print "A.dtype: "
print A.dtype
print "A.itemsize"
print A.itemsize
print "A.data"
print A.data

运行上述代码可以得到如下结果：

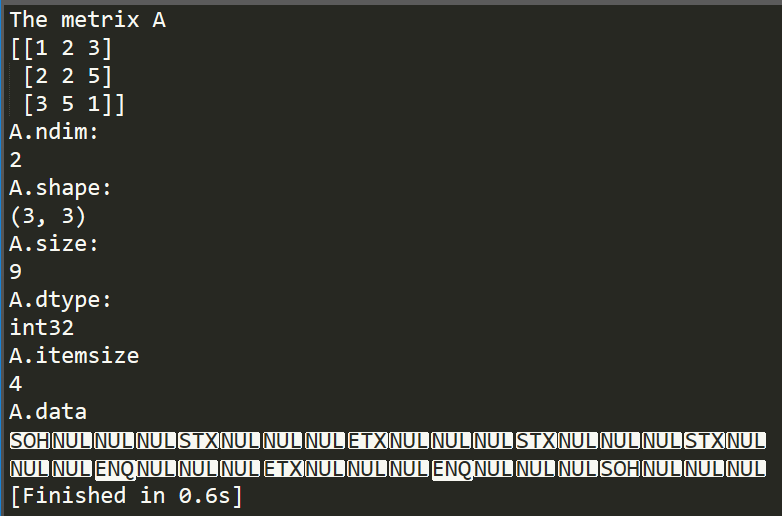
从上述结果可知，indim属性表征的是一个矩阵的维度，即一个矩阵中的元素最多能用多少个矩阵下标来表示，在这里，由于是二维矩阵，因此，该值为2。如果是三维矩阵，那么一个元素需要3个索引值来表示，那么indim属性值也就为3。shape属性表示的是n*m矩阵的尺寸，在这里是个3*3矩阵，因此该值为（3， 3），则该值的长度即为indim值。size表示的是这个矩阵中包含的元素的个数，该属性与shape属性有着相同的表征含义。dtype则表示的是矩阵中元素的数据类型。itemsize则表示的是一个元素的字节数，在这里由于是32位整型，因此，该值为32/8 = 4。data属性表示的是矩阵所对应的缓存中的实际数据，一般来说是用不到这个属性的。

 除了以上内容，我们在学习线性代数的过程中，通常会遇到一些计算的小技巧，比如借助单位矩阵来求一些矩阵等，下面还是以线代中的一些例子为例。

ex2:

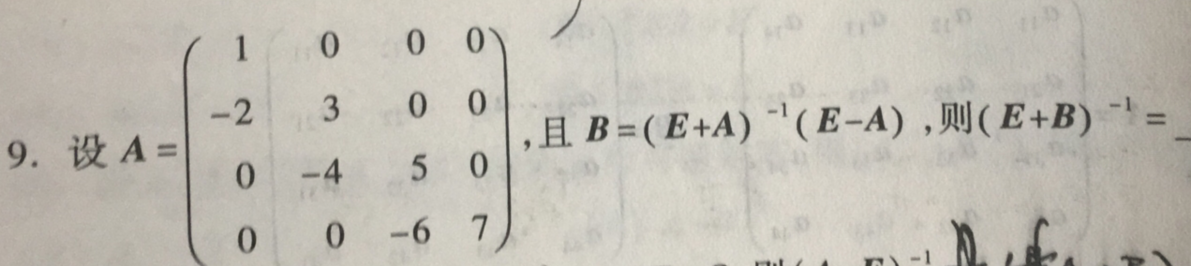
上题中需要用到一个单位矩阵E，在numpy中，提供了相应的方法来生成一定要求的矩阵，下面结合例子来调用输出这些方法。

首先，给出numpy中自带的一些创建特殊矩阵的方法：

# Create an array full of zeros, the type of parameter likes np.shape.
Zero = np.zeros((3, 3))
print "Zero array: "
print Zero

# The function ones creates an array full of ones
ones = np.ones((4, 4))
print "Ones array: "
print ones

# The function empty creates an array whose initial content is
# random and depends on the state of the memory. By default, 
# the dtype of the created array is float64.

Empty = np.empty((3, 3))
print "Empty array: "
print Empty

# To creates sequences of numbers, this function
# analogous to range  that returns arrays instead of lists.
Sequences = np.arange(10, 30, 2)
print "Sequences array: "
print Sequences

# The function creates a sequences array by predicting the 
# number of elements obtained.
Linspace = np.linspace(10, 30, 25)
print "Linspace array: "
print Linspace

# The function creates a N-th order identity matrix.
E = np.eye(4)
print "E array: "
print E

运行以上代码可以得到如下输出结果：

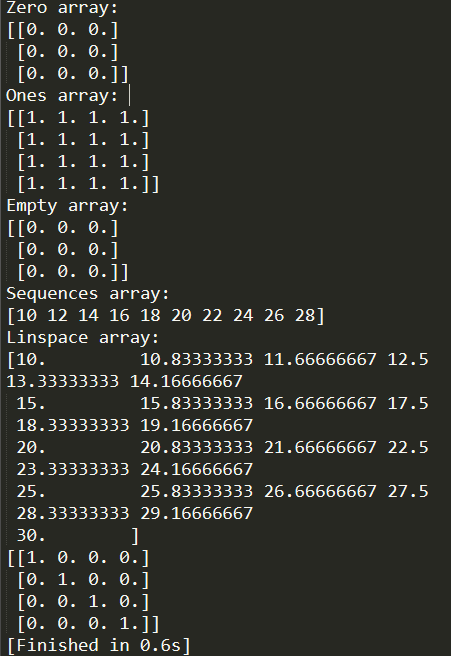
从上图可以看到:

• np.zeros(parameter A)的方式，可以创建一个n*m型的零矩阵。这个A类似之前输出的属性shape，一个元组形式的参数，当然，n*m只是举例说明，实际可以是多维的，如(i, j, k)。
• np.ones(parameter A)与zeros（）函数相同，所传参数也是一个元组类型数据，只是结果有所不同，生成的是一个全1的矩阵。
• np.empty(parameter A)创建的是一个随机数矩阵，所传参数与zeros和ones相同，只是生成的结果是一个随机数构成的矩阵，内部元素的数据与内存有关，数据类型默认是64位浮点型。
• np.arange(parameter A)创建的是一个等差序列list，参数A是一个包含三个数据的元组，(a,b,c)，[a，b)为这个arange的范围，左闭右开区间，即不包括b的，步长为c的一个序列。
• np.linspace(parameter A)则是创建一个等差序列list，与arange不同的是，这里参数A依旧是(a, b, c)，但是，这个元组中的c变量表示的不是步长，而是从a到b这个左开右闭区间内，所包含的数的个数。
• np.eye(parameter A)创建的一个N阶的单位矩阵，参数A为一个整型数据，表示的是单位矩阵的阶数。

此外，numpy中创建的矩阵也是可以对其进行python中的切片和迭代操作的。

结合以上的内容，可以非常方便的创建一个单位矩阵E，进而求解所给出的那道题。代码如下所示：

A = np.array([[1, 0, 0, 0], [-2, 3, 0, 0],
             [0, -4, 5, 0], [0, 0, -6, 7]])

E = np.eye(4)

C = lg.inv((E + A))
B = C.dot((E - A))
E_add_B_inv = lg.inv((E + B))
print E_add_B_inv

运行上述代码，即可求得：

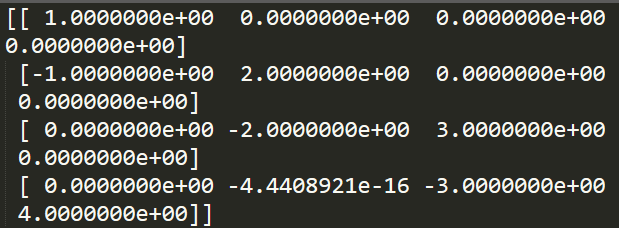
可以看到，所求结果与手算结果相一致，第四行第二列的那个数值直接视为0。

补充：

在numpy中，每个np对象还包含转置操作：

A = np.array([[1, 0, 0, 0], [-2, 3, 0, 0],
             [0, -4, 5, 0], [0, 0, -6, 7]])
print "The transposition of A: "
print A.T

得到结果如下所示：

以上是目前的我本人所需要用到的一些numpy的知识点，后续随着学习的深入会继续补充该文。还有更多的内容，中文版的入门教程可以参考这篇博客https://www.cnblogs.com/qflyue/p/8244331.html

英文版的可以直接查官方的文档了

https://docs.scipy.org/doc/numpy-dev/user/quickstart.html