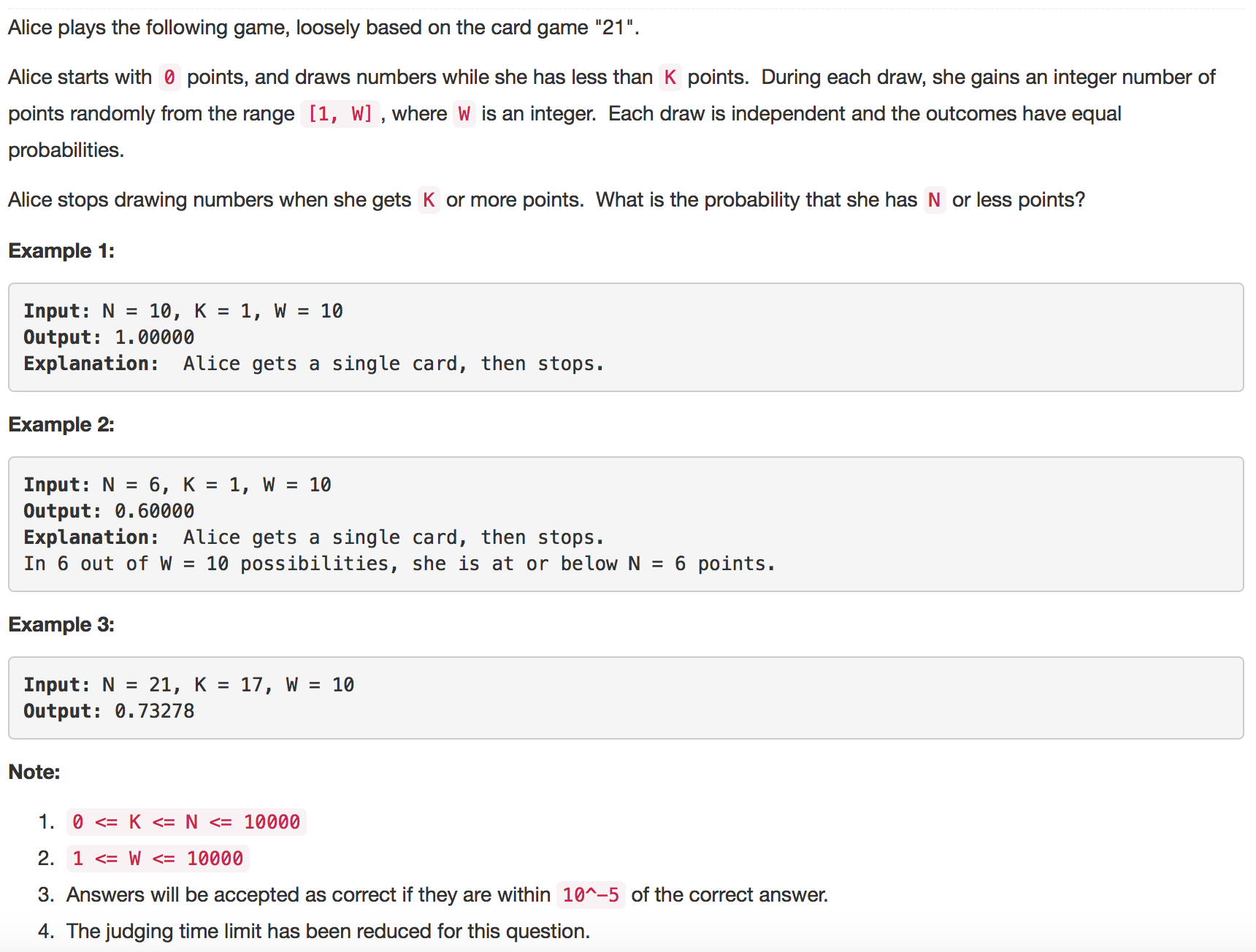
题目如下:
解题思路:这个题目有点像爬楼梯问题,只不过楼梯问题要求的计算多少种爬的方式,但是本题是计算概率。因为点数超过或者等于K后就不允许再增加新的点数了,因此我们可以确定最终Alice拥有的点数的区间是[K,K-1+W],下限等于K很好理解,Alice最后一次抽取点数前可能拥有的点数最大值是K-1,最后一次抽取的点数最大值是W,因此上限就是K-1+W。和爬楼梯类似,恰好获得点数n的概率dp[n] = sum(dp[n-w]/w + dp[n-w+1]/w + .... dp[n-1]/w)。因为获取任意一个点数的概率都是1/W,所以上面的公式中每个dp都要除以W。但是题目约定了一个K值,在n > k + 1的情况下,dp[n]是无法通过dp[n-1]得到,需要修正公式: dp[n] = sum(dp[n-w]/w + dp[n-w+1]/w + .... dp[K-1]/w)。最后,点数小于或者等于N的概率就是 sum(dp[K:N + 1])。
代码如下:
class Solution(object): def new21Game(self, N, K, W): """ :type N: int :type K: int :type W: int :rtype: float """ low = K high = K - 1 + W if N < low or K == 0 or N > high: return 1.0 dp = [0 for x in xrange(high + 1)] dp[0] = 0.0 for i in xrange(1, min(high, W) + 1): dp[i] = float(1) / float(W) # print dp pro = 0.0 for i in xrange(2, W + 1): if i > K: maxv = K - 1 minv = max(i - W, 1) else: maxv = i - 1 minv = max(i - W, 1) if pro == 0.0: for j in xrange(minv, maxv + 1): pro += dp[j]/W else: if i > K: pro -= dp[minv-1]/W else: pro += dp[maxv]/W pro -= dp[minv-1]/W dp[i] += pro lastWCount = sum(dp[:min(K, W + 1)]) #print lastWCount for i in xrange(W + 1, len(dp)): dp[i] = lastWCount / W if i < K: lastWCount += dp[i] lastWCount -= dp[i - W] #print '1:',i,dp[i] #print 'total:',sum(dp[low:]) #print '1',dp[K-5:K+5] #print dp return sum(dp[low:N + 1])/sum(dp[low:])