题目如下:
Given a rectangular cake with height
hand widthw, and two arrays of integershorizontalCutsandverticalCutswherehorizontalCuts[i]is the distance from the top of the rectangular cake to theithhorizontal cut and similarly,verticalCuts[j]is the distance from the left of the rectangular cake to thejthvertical cut.Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays
horizontalCutsandverticalCuts. Since the answer can be a huge number, return this modulo 10^9 + 7.Example 1:
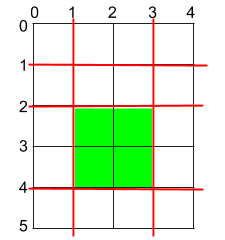
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] Output: 4 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts.
After you cut the cake, the green piece of cake has the maximum area.Example 2:
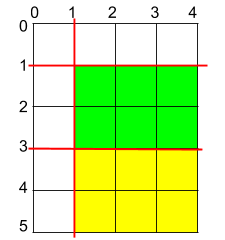
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] Output: 6 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.Example 3:
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] Output: 9Constraints:
2 <= h, w <= 10^91 <= horizontalCuts.length < min(h, 10^5)1 <= verticalCuts.length < min(w, 10^5)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- It is guaranteed that all elements in
horizontalCutsare distinct.- It is guaranteed that all elements in
verticalCutsare distinct.
解题思路:本题其实很简单,只要分别找出horizontalCuts和verticalCuts相邻的两个元素的最大差值,再计算这两个差值的成绩即可。
代码如下:
class Solution(object): def maxArea(self, h, w, horizontalCuts, verticalCuts): """ :type h: int :type w: int :type horizontalCuts: List[int] :type verticalCuts: List[int] :rtype: int """ horizontalCuts.sort() verticalCuts.sort() if horizontalCuts[0] != 0:horizontalCuts.insert(0,0) if horizontalCuts[-1] != h:horizontalCuts.append(h) if verticalCuts[0] != 0:verticalCuts.insert(0,0) if verticalCuts[-1] != w:verticalCuts.append(w) max_h,max_w = 0,0 for i in range(1,len(horizontalCuts)): max_h = max(max_h,horizontalCuts[i] - horizontalCuts[i-1]) for i in range(1,len(verticalCuts)): max_w = max(max_w,verticalCuts[i] - verticalCuts[i-1]) return (max_h * max_w) % (10**9+7)