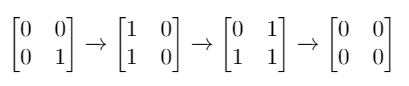题目如下:
Given a
m x nbinary matrixmat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.Return the minimum number of steps required to convert
matto a zero matrix or -1 if you cannot.Binary matrix is a matrix with all cells equal to 0 or 1 only.
Zero matrix is a matrix with all cells equal to 0.
Example 1:
Input: mat = [[0,0],[0,1]] Output: 3 Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.Example 2:
Input: mat = [[0]] Output: 0 Explanation: Given matrix is a zero matrix. We don't need to change it.Example 3:
Input: mat = [[1,1,1],[1,0,1],[0,0,0]] Output: 6Example 4:
Input: mat = [[1,0,0],[1,0,0]] Output: -1 Explanation: Given matrix can't be a zero matrixConstraints:
m == mat.lengthn == mat[0].length1 <= m <= 31 <= n <= 3mat[i][j]is 0 or 1.
解题思路:最大就是3*3的矩阵,BFS把每种情况都试一遍就好了。
代码如下:
class Solution(object): def minFlips(self, mat): """ :type mat: List[List[int]] :rtype: int """ import copy def isAllZero(grid): count = 0 for i in grid: count += sum(i) return count == 0 def encode(grid): grid_s = '' for i in range(len(grid)): for j in range(len(grid[i])): grid_s += str(grid[i][j]) if i != len(grid) - 1 : grid_s += '#' return grid_s def decode(grid_s): gl = grid_s.split('#') grid = [] for i in gl: tl = [] for j in list(i): tl.append(int(j)) grid.append(tl) return grid res = float('inf') queue = [(encode(mat),0)] dic = {} dic[encode(mat)] = 0 while len(queue) > 0: gs,step = queue.pop(0) grid = decode(gs) if isAllZero(grid): res = min(res,step) continue elif res <= step: continue for i in range(len(grid)): for j in range(len(grid[i])): #if grid[i][j] == 0: continue new_grid = copy.deepcopy(grid) if new_grid[i][j] == 1: new_grid[i][j] = 0 else:new_grid[i][j] = 1 directions = [(1, 0), (-1, 0), (0, 1), (0, -1)] for (x, y) in directions: if x + i >= 0 and x + i < len(grid) and y + j >= 0 and y + j < len(grid[0]): if new_grid[x + i][y + j] == 0: new_grid[x + i][y + j] = 1 else: new_grid[x + i][y + j] = 0 encode_Str = encode(new_grid) if encode_Str not in dic or dic[encode_Str] > step + 1: queue.append((encode(new_grid), step + 1)) dic[encode_Str] = step + 1 return res if res != float('inf') else -1