回归分析用于分析输入变量和输出变量之间的一种关系,其中线性回归是最简单的一种。
设: Y=wX+b,现已知一组X(输入)和Y(输出)的值,要求出w和b的值。
举个例子:快年底了,销售部门要发年终奖了,销售员小王想知道今年能拿多少年终奖,目前他大抵知道年终奖是和销售额(特征量)挂钩的,具体什么规则不清楚,那么他大概有两个方法解决这个问题:
1、去问老板,今年的分配规则是什么。【通过算法解决问题】
2、去向同事打听他们的销售额和奖金情况,然后推算自己能拿多少。【通过数据解决问题】
我们当然选择第二种方法了。通过收集数据,我们得到下面这个表格:

拿到这个数据,我们基本上很快就能推算出两者的对应关系,如果推算不出来,我们也可以绘制下面这张图表:
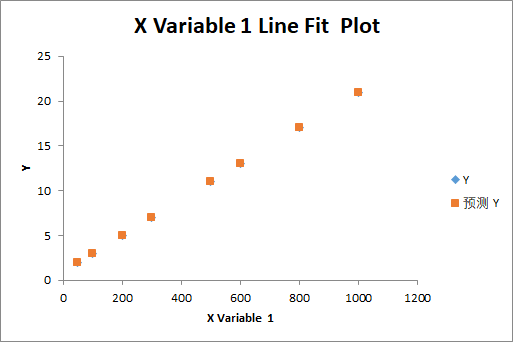
通过图表,我们可以立即看出两者的对应关系了。
以上就是一个典型的线性回归求解的问题,下面我们要用TensorFlow框架解决这个问题。
具体解决思路如下:
1、先设w=1,b=0
2、取得一批训练数据,将X代入函数f(x)=wx+b,计算取得在当前条件下的预测值Y‘
3、计算预测值Y‘和实际值Y的误差
4、根据梯度对w、b进行微调
5、重复上述步骤,直到误差值足够小。
先贴出全部代码,然后再逐一解释。
public class LinearRegression { public void Run() { // Supper Parameters float learning_rate = 0.01f; var W = tf.Variable<float>(1); var b = tf.Variable<float>(0); int epochs = 30; int steps = 100; Tensor loss = null; for (int epoch = 0; epoch < epochs; epoch++) { for (int step = 0; step < steps; step++) { int batch_size = 10; (NDArray train_X, NDArray train_Y) = LoadBatchData(batch_size); using (var g = tf.GradientTape()) { //通过当前参数计算预测值 var pred_y = W * train_X + b; //计算预测值和实际值的误差 loss = tf.reduce_sum(tf.pow(pred_y - train_Y, 2)) / batch_size; //计算梯度 var gradients = g.gradient(loss, (W, b)); //更新参数 W.assign_sub(learning_rate * gradients.Item1); b.assign_sub(learning_rate * gradients.Item2); } } Console.WriteLine($"Epoch{epoch + 1}: loss = {loss.numpy()}; W={W.numpy()},b={b.numpy()}"); } } public (NDArray, NDArray) LoadBatchData(int n_samples) { float w = 0.02f; float b = 1.0f; NDArray train_X = np.arange<float>(start: 1, end: n_samples + 1); NDArray train_Y = train_X * w + b; return (train_X, train_Y); } }
下面对代码进行简单的解释:
首先,我们要读取一批(比如10组 )训练数据,标记为:train_X和train_Y,然后通过现有的w和b值计算预测值:pred_Y=w*train_X+b,此时train_X、train_Y、pred_Y都是10个数据长度的数组。
然后计算预测数据和时间数据之间的误差,我们采用均方误差公式来计算:
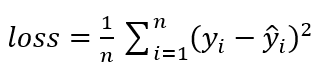
然后开始计算W、b对于loss函数的梯度,梯度表达的就是W、b的变化对计算结果的影响,比如将W增大一点,loss的计算结果是变大还是变小,我们的目标是希望loss的值最小,如果w变大时loss变大(梯度为正数),那么我们下一次就将w变小一点,反之同理。
![]()
这里的learning_rate表示学习率,表示每次参数进行调整的步进值,就是每次调整一大步,还是一小步。通过多次的循环调整,w和b的值将调整为一个合适的数字,此时loss的值将会很小,线性回归就完成了。以下是运算结果:
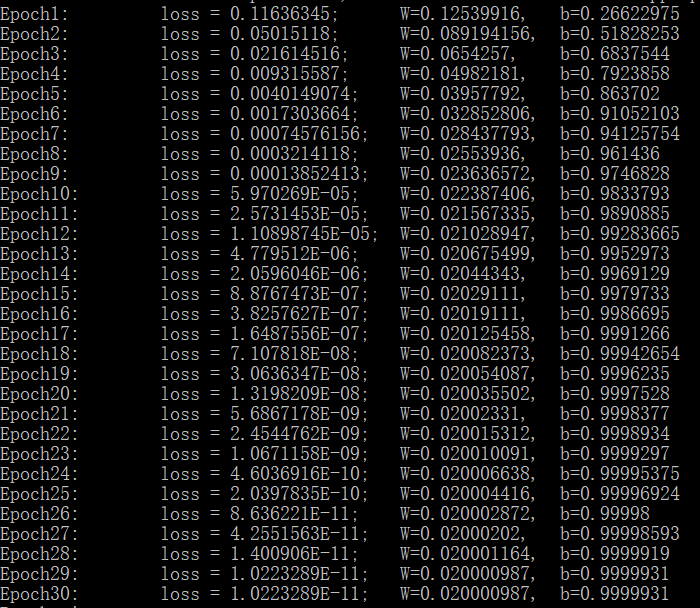
在上述过程中,最难理解的就是梯度,以及如何计算梯度的问题,想要进一步了解的话可以参阅相关参考资料。
【相关资源】
源码:Git: https://gitee.com/seabluescn/tf_not.git
项目名称:LinearRegression
【参考资料】
《深度学习入门:基于Python的理论与实践(斋藤康毅)》,网上可以找到电子版