带修改的莫队

带修改的莫队

【数颜色】

墨墨购买了一套N支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

1、 Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔。

2、 R P Col 把第P支画笔替换为颜色Col。

为了满足墨墨的要求，你知道你需要干什么了吗？

就是在基础的莫队上增加了修改操作

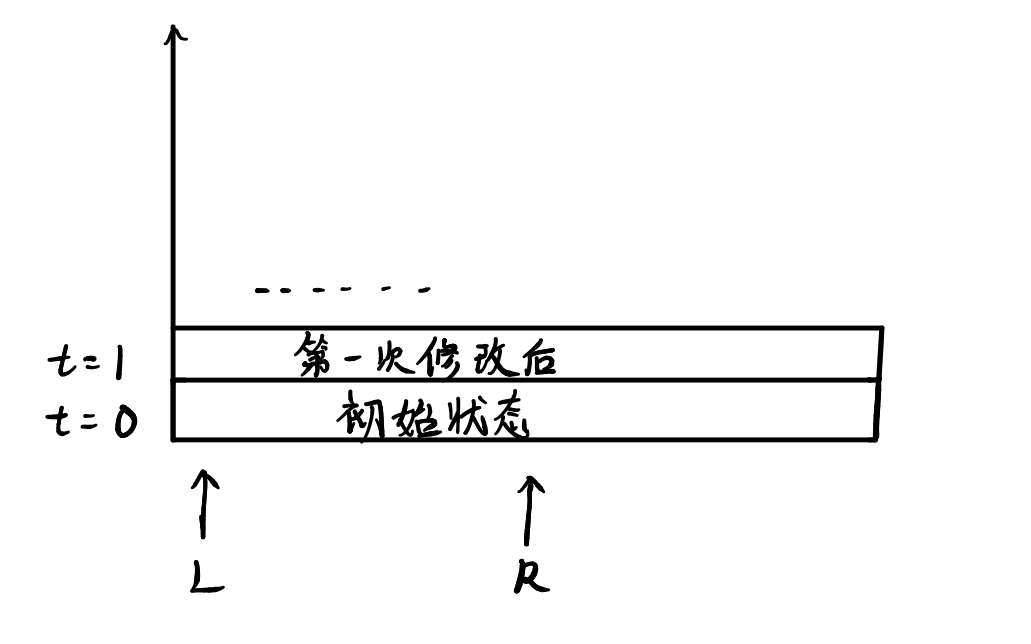
所以需要挪动三个指针 (L) , (R) , (t)

有个小技巧

while (t < qt) {
    t++;
    if (ql <= m[t].pos and m[t].pos <= qr) {
        del(A[m[t].pos]);
        add(m[t].val);
    }
    swap(A[m[t].pos], m[t].val);
}
while (t > qt) {
    if (ql <= m[t].pos and m[t].pos <= qr) {
        del(A[m[t].pos]);
        add(m[t].val);
    }
    swap(A[m[t].pos], m[t].val);
    t--;
}

这个 (swap) 操作就很灵性

块大小为 (^3sqrt {nt}) 的时候达到理论最快复杂度， 然而我 (TLE) 了 wrnm

我这份代码 len = cbrt(1.0 * n * mcnt) + 1; 会被卡一个点

前两个块大小 (n ^ {frac 2 3}) 和 (n^{frac 3 4}) 都可以通过, 0.75跑的最快。

改成第三份理论最优就 TLE ？ 难道又是我的毒瘤代码的锅

//len = pow(n ,0.6667);
len = pow(n, 0.75);
//len = pow(n * mcnt, 0.333) + 1;

/*
 * @Author: zhl
 * @Date: 2020-11-19 10:39:02
 */
#include<bits/stdc++.h>
using namespace std;

const int N = 150000;
int A[N], cnt[1000010], block[N];
int n, mm, len;
struct query {
	int id, l, r, t;
	bool operator < (const query& rhs)const {
		int al = block[l], bl = block[rhs.l];
		int ar = block[r], br = block[rhs.r];
		if (al != bl)return al < bl;
		if (ar != br)return ar < br;
		return t < rhs.t;
	}
}q[N];
struct modify {
	int pos, val;
}m[N];
long long qcnt, mcnt, ans[N], now;

void del(int x) {
	if (!--cnt[x])now--;
}
void add(int x) {
	if (!cnt[x]++)now++;
}
signed main() {
	scanf("%d%d", &n, &mm);
	for (int i = 1; i <= n; i++)scanf("%d", A + i);

	while (mm--) {
		char op[2]; int a, b;
		scanf("%s%d%d", op, &a, &b);
		if (*op == 'Q') {
			qcnt++;
			q[qcnt] = { qcnt,a,b, mcnt };
			//q[qcnt] = { ++qcnt,a,b,mcnt };
		}
		else {
			m[++mcnt] = { a,b };
		}
	}
	len = pow(n ,0.6667);
	for (int i = 1; i <= n; i++)block[i] = i / len;
	sort(q + 1, q + 1 + qcnt);
	int l = 1, r = 0, t = 0;

	for (int i = 1; i <= qcnt; i++) {
		int ql = q[i].l, qr = q[i].r, qt = q[i].t;
		while (l < ql) del(A[l++]);
		while (l > ql) add(A[--l]);
		while (r < qr) add(A[++r]);
		while (r > qr) del(A[r--]);

		while (t < qt) {
			t++;
			if (ql <= m[t].pos and m[t].pos <= qr) {
				del(A[m[t].pos]);
				add(m[t].val);
			}
			swap(A[m[t].pos], m[t].val);
		}
		while (t > qt) {
			if (ql <= m[t].pos and m[t].pos <= qr) {
				del(A[m[t].pos]);
				add(m[t].val);
			}
			swap(A[m[t].pos], m[t].val);
			t--;
		}
		ans[q[i].id] = now;
	}
	for (int i = 1; i <= qcnt; i++)printf("%d
", ans[i]);
}