单链表逆置

方法一：非递归方法，利用辅助指针，时间复杂度为O(n)

程序如下：

template <typename Type>
struct ListNode {
    Type data;
    ListNode* next;
    ListNode(Type pdata) :data(pdata), next(nullptr) {}
};

template <typename Type>
void reverseList(ListNode *node)
{
    ListNode *currPos = node, *nextPos = node->next, *prevPos = nullptr;
    while (nextPos != nullptr)
    {
        // 改变currPos->next
        currPos->next = prevPos;

        // 依次更新prev、curr、next（向后移动）
        prevPos = currPos;
        currPos = nextPos;
        nextPos = nextPos->next;
    }
    currPos->next = prevPos; // 注意最后一步
    return currPos;
}

上面的过程如果不画图的话，很容易搞晕，所以我绘制了下面的过程图便于理解：

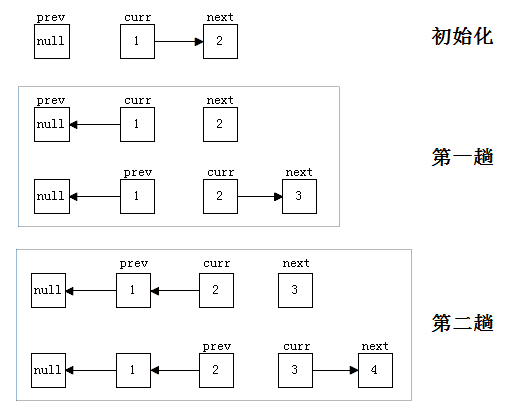
方法二：递归方法

template <typename Type>
struct ListNode {
    Type data;
    ListNode* next;
    ListNode(Type pdata) :data(pdata), next(nullptr) {}
};

template <typename Type>
void reverseList_recur(ListNode *currPos)
{
    // 空链表
    if (currPos == nullptr)
        return;
    // 基准情形，也就是递归结束条件
    if (currPos->next == nullptr)
        return;
    ListNode *nextPos = currPos->next;

    reverseList_recur(nextPos);

    nextPos->next = currPos;
    currPos->next = nullptr;
}

递归方法还是比较难以理解的，知道栈帧的概念的话会容易很多。每次函数调用都会在栈空间push一块空间，这个空间会保存该函数的形参和局部变量，当函数结束后，才会pop出这块空间。

也就是说，每次递归调用中的形参 currPos，局部变量nextPos都保存下来，直到基准情形出现。会产生多个currPos、nextPos变量，加上函数调用产生的其他指针和空闲空间等等。会占用更多的内存空间，而且函数调用会产生更多操作，时间开销很大。当然，并不排除有些编译器会优化掉递归的函数调用过程。

所以，递归方法并不推荐。递归的图示绘制相对复杂，这里不再演示。