大意:给你一个平面上N(N<=100000)个点,问相切于x轴的圆,将所有的点都覆盖的最小半径是多少。
计算几何???Div2的D题就考计算几何???某人昨天上课才和我们说这种计算几何题看见就溜。。。。
打完比赛才发现好像并不用计算几何,实则是一个二分答案的水题。。
发现如果点在x轴两侧就肯定不行,所以我们把所有的点都挪到一侧。
我们二分一个半径,然后发现因为圆相切于x轴,那么这个圆的圆心一定在y=r的直线上移动。
对于所有的点,它可以被如图的线段AC上的点覆盖,点在AC下方也同理。(终于有个图是我自己画的了。。。)
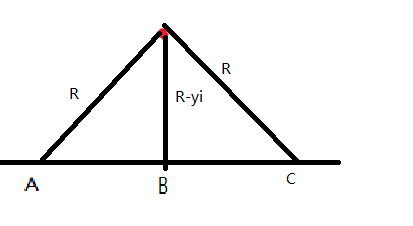
然后发现圆心的取值就在xi±√(R2-(R-yi)2)之间。
所以说把每个点的可取圆心的点的集合的交算出来,看看是不是空集,不是空集就可行。

#include <iostream> #include <algorithm> #include <cmath> #include <cstdio> using namespace std; const double eps=1e-8; int n; struct Node {int x,y;}node[100005]; bool flag; bool ck(double mid) { double l=-1e18,r=1e18; for(int i=1;i<=n;i++) { if(node[i].y>mid+mid) return 0; double range=sqrt(node[i].y*(2*mid-node[i].y)); l=max(l,node[i].x-range);r=min(r,node[i].x+range); } return (l-r+eps)<=0; } int main() { scanf("%d",&n); scanf("%d%d",&node[1].x,&node[1].y); if(node[1].y<0) flag=1;node[1].y=abs(node[1].y); for(int i=2;i<=n;i++) { scanf("%d%d",&node[i].x,&node[i].y); if(flag&&node[i].y>0){puts("-1") ;return 0;} if(flag==false && node[i].y<0) {puts("-1");return 0;} node[i].y=abs(node[i].y); } double l=0,r=1e18;int cnt=300; while(cnt--) { double mid=(l+r)/2; if(ck(mid)) r=mid; else l=mid; } printf("%lf",l); }
