Problem Description
The little cat takes over the management of a new park. There is a large circular statue in the center of the park, surrounded by N pots of flowers. Each potted flower will be assigned to an integer number (possibly negative) denoting how attractive it is. See the following graph as an example:
(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)
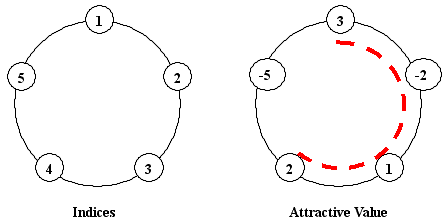
The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions.
Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.
(Positions of potted flowers are assigned to index numbers in the range of 1 ... N. The i-th pot and the (i + 1)-th pot are consecutive for any given i (1 <= i < N), and 1st pot is next to N-th pot in addition.)

The board chairman informed the little cat to construct "ONE arc-style cane-chair" for tourists having a rest, and the sum of attractive values of the flowers beside the cane-chair should be as large as possible. You should notice that a cane-chair cannot be a total circle, so the number of flowers beside the cane-chair may be 1, 2, ..., N - 1, but cannot be N. In the above example, if we construct a cane-chair in the position of that red-dashed-arc, we will have the sum of 3+(-2)+1+2=4, which is the largest among all possible constructions.
Unluckily, some booted cats always make trouble for the little cat, by changing some potted flowers to others. The intelligence agency of little cat has caught up all the M instruments of booted cats' action. Each instrument is in the form of "A B", which means changing the A-th potted flowered with a new one whose attractive value equals to B. You have to report the new "maximal sum" after each instruction.
Input
There will be a single test data in the input. You are given an integer N (4 <= N <= 100000) in the first input line.
The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position.
A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above.
Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer.
The second line contains N integers, which are the initial attractive value of each potted flower. The i-th number is for the potted flower on the i-th position.
A single integer M (4 <= M <= 100000) in the third input line, and the following M lines each contains an instruction "A B" in the form described above.
Restriction: All the attractive values are within [-1000, 1000]. We guarantee the maximal sum will be always a positive integer.
Output
For each instruction, output a single line with the maximum sum of attractive values for the optimum cane-chair.
Sample Input
5
3 -2 1 2 -5
4
2 -2
5 -5
2 -4
5 -1
Sample Output
4
4
3
5
***************************************************************************************************************************
一个圆环上有n(4<= n <= 100000)个数字,编号依次从1到n,第n个数与第1个数相连。规则是:从环上选取任意个数(但不能为0也不能取全部)的连续数字,使选取数字之和最大。但现在有m(4<= m <= 100000)个操作,用a, b两个数字来描述, 意思是:将环上编号为a的数字换成b。现要求每次操作后都按照规则输出最大之和
,将情况分成两种。
1. 圆环上的数全是正数。所有数字之和减去其中最小的一个数,即为结果。
2. 圆环上的数有负数。此时有两种选取数字的方式:
1. 所选的连续数字包含编号1和n的两个数。此时在线段树内他们并不连续(在1和n之间被断开了)。所有数字之和减去线段树区间内数字最小之和即为结果。
2. 所选的连续数字不包含1和n两个数。用线段树维护出区间内最大连续数字之和即可。
线段树需要维护7个数据:sum, lmax, rmax, tmax, lmin, rmin, tmin。
其中lmax意为从区间左端第一个数开始的最大连续数字之和,rmax意为从区间右端第一个数开始的最大连续数字之和,tmax意为整个区间的最大连续数字之和。 min同理。
至于条件判定,当圆环上全是正数时,对于整个区间有sum=tmax。
***************************************************************************************************************************

1 #include <iostream> 2 #include <string> 3 #include <cstring> 4 #include <cstdio> 5 #include <cmath> 6 #define ls rt<<1 7 #define rs rt<<1|1 8 #define lson l,m,ls 9 #define rson m+1,r,rs 10 #define mid (l+r)>>1 11 #define MAXN 100010 12 using namespace std; 13 int N,M; 14 int a[MAXN]; 15 struct node 16 { 17 int l,r; 18 int lmax,rmax,summax; 19 int lmin,rmin,summin; 20 int sum; 21 }tree[MAXN<<2]; 22 void pushup(int rt) 23 { 24 tree[rt].sum=tree[ls].sum+tree[rs].sum; 25 26 tree[rt].lmax=max(tree[ls].lmax,tree[ls].sum+tree[rs].lmax); 27 tree[rt].rmax=max(tree[rs].rmax,tree[rs].sum+tree[ls].rmax); 28 tree[rt].summax=max(max(tree[ls].summax,tree[rs].summax),tree[ls].rmax+tree[rs].lmax); 29 30 tree[rt].lmin=min(tree[ls].lmin,tree[ls].sum+tree[rs].lmin); 31 tree[rt].rmin=min(tree[rs].rmin,tree[rs].sum+tree[ls].rmin); 32 tree[rt].summin=min(min(tree[ls].summin,tree[rs].summin),tree[ls].rmin+tree[rs].lmin); 33 34 } 35 void build(int l,int r,int rt) 36 { 37 if(l>r)return; 38 tree[rt].l=l; 39 tree[rt].r=r; 40 if(r==l) 41 { 42 tree[rt].sum=a[l]; 43 tree[rt].lmax=tree[rt].lmin=tree[rt].summax=a[l]; 44 tree[rt].rmin=tree[rt].rmax=tree[rt].summin=a[l]; 45 return; 46 } 47 int m=(l+r)>>1; 48 build(lson); 49 build(rson); 50 pushup(rt); 51 } 52 53 void update(int pos,int val,int rt) 54 { 55 if(tree[rt].l==tree[rt].r&&tree[rt].l==pos) 56 { 57 tree[rt].sum=val; 58 tree[rt].lmax=tree[rt].lmin=tree[rt].rmin=tree[rt].rmax=val; 59 tree[rt].summax=tree[rt].summin=val; 60 return; 61 } 62 int m=(tree[rt].l+tree[rt].r)>>1; 63 if(m<pos) 64 update(pos,val,rs); 65 else 66 update(pos,val,ls); 67 pushup(rt); 68 } 69 70 int main() 71 { 72 while(scanf("%d",&N)!=EOF) 73 { 74 for(int i=1;i<=N;i++) 75 scanf("%d",&a[i]); 76 build(1,N,1); 77 78 scanf("%d",&M); 79 int pos,val; 80 81 while(M--) 82 { 83 scanf("%d%d",&pos,&val); 84 update(pos,val,1); 85 86 if(tree[1].sum==tree[1].summax) 87 printf("%d ",tree[1].sum-tree[1].summin); 88 else 89 printf("%d ",max(tree[1].summax,tree[1].sum-tree[1].summin)); 90 } 91 } 92 return 0; 93 }
