题目
WZJ题解
T1
T2
T3
后缀自动机+($parents$ 树)树链剖分
发现有大量子串需要考虑,考虑摁死子串的一端。
首先,这题显然是一道离线题,因为所有的询问都是 $1$ 到 某个数,也就是一个前缀和,完全可以递推处理。
所以先把所有的询问按 $m$ 从小到大排序。
然后我们画画 $KMP$ 树,发现一些神奇的性质。
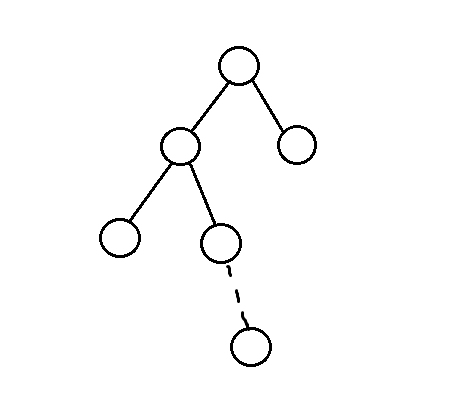
设虚边下面那个点为新加入的一个点(字符),如果这个点的编号(编号 即插入的这个字符是原串的第几位) 比这棵树上面原有的那些点的编号都大的话,那它一定会成为叶子节点。
也就是说,如果你按顺序依次插入原串的每一位字符,每个新加入的字符一定都会加到树的叶子处。
这样的话,上面那些以前插入的节点的深度都没有变,新加入一个点不会对之前的任何点的贡献造成影响。
所以所有右端点范围在 $[1,i]$ 内的子串的答案 就是所有右端点范围在 $[1,i-1]$ 内的子串的答案 $+$ 所有右端点在第 $i$ 位的子串的答案。
这个可以二维前缀和递推求,即开一个 $fakeans$ 动态累加 所有右端点范围在 $[1,i]$ 内的子串的答案,再开一个 $ans$ 动态累加累加 $fakeans$,这样就算上了每一位固定为右端点 且左端点任意时的所有子串,即所有左右端点情况的子串。
我们考虑加入第 $i$ 位字符时,这个字符对答案的贡献怎么算。
由于加入的这个字符一定在树的最底下(叶子),所以它的深度就是 树

如图,也就是以原串第 $i$ 位为结尾的 $i$ 个后缀串。