大概就是全场就我写不过 $FFT$ 系列吧……自闭
T1
奶一口,下次再写不出这种 $NTT$ 裸题题目我就艹了自己 -_-|||
而且这跟我口胡的自创模拟题 $set1$ 的 $T3$ 差不多啊……我之前口胡那题甚至还改简单了点(因为忘了 $FFT$ 可以套分治优化)。
注意,分治 + $FFT$ ≠ 分治$FFT$ !!!
分治 + $FFT$ 是用分治来卷一堆背包,并且这些背包的总大小是祖传级别的!!!
分治$FFT$ 跟 $FFT$ 求的式子都不一样。
基础知识:n点无根树,问包含恰好k个点的连通子图的最大权,点上有权,k∈[1,n]。
$f(x,k)$ 以 $x$ 为根子树包含 $k$ 个点的最大权。
这就是以前说过的那个假 $O(n^3)$ 复杂度的 $dp$,不说了。
这题其实就是给了一堆环,然后问随机放 $k$ 个人,使每个环上至少有 $1$ 个人的概率。
像这种概率问题,我们先把它转化成方案数,因为 概率 $=$ 满足要求的方案数 $/$ 总方案数。
一提到方案数,我们就想到这个可以用传统的背包做……
就是对于每个环,预处理出在这个环上分别放 $1$ 到 $size$ 个人的方案数。
可以证明这样全局有 $n$ 个方案数。
然后就要用一种类似于合并背包的方法,把这堆总大小为 $n$ 的背包合并成一个。
啥叫合并背包?
考虑这么一个问题:有两个背包各自维护一个集合,背包的第 $i$ 位表示 自己的集合中有多少个值为 $i$ 的数。
然后让你求 两集合的所有数两两配对相加后,得到的数的集合。
假设一个集合中有 $x$ 个值为 $i$ 的数,另一个集合中有 $y$ 个值为 $j$ 的数,根据题意(两两配对相加)和乘法原理,可知新集合会有 $x imes y$ 个值为 $i+j$ 的数。
由于需要用两重循环枚举两个背包中配对的数,所以时间复杂度是 $O(n^2)$。
这就是合并背包。
但这样合并的时间显然升天了!怎么优化?
其实合并背包有个定性优化,我们只需要观察合并背包的式子就发现了——
$$C_{i+j}=sum_{i=1}^{size(A)} sum_{j=1}^{size(B)} A_i imes B_j$$
这就是裸的 $FFT$ 式子啊!此时合并两个背包的时间复杂度只有 $O(n imes log(n))$ 了(有一堆常数)。
但是这题有一堆背包,那时间复杂度还要再乘个玄学值,可能会超时。
所以考虑快速合并大量背包的做法。这里有两种,一种是 分治+$FFT$,一种是 按秩合并(即每次合并两个大小最小的背包)。
分治+$FFT$ 就是分治合并一堆背包,时间复杂度是 $O(n imes log^2(n))$ 带巨大常数(因为分治的每层中,合并一些总长为 $n$ 的背包的总时间复杂度略高于 $O(n imes log(n))$);
按秩合并(启发式合并)类似于哈夫曼编码的原理,这种做法的时间复杂度其实比较玄学,但实测跟 分治+$FFT$ 的效率差不多。
由于这题需要取模,所以把 $FFT$ 全改成 $NTT$。
T2
防 $AK$ 题
$30pts$ 轮廓线 $dp$ 裸题。
$50pts$ 改进一下,一行一行转,那么枚举相邻两行的所有状态,预处理一个 $(2^m)^2$ 大小的转移矩阵。然后矩阵快速幂转移。时间复杂度 $O((2^m)^3 imes log(n))$。
$65pts$ 发现 $log$ 直接爆出去了,所以二进制快速幂改成十进制快速幂。
$0$ 到 $9$ 分成 $2$ 的若干次方
原理……像循环展开吧。
$80pts$ 把那些没用的转移去掉。
具体怎么去掉呢?我们发现每次转移既然都是对应一个固定的转移矩阵,也就是说每相邻两层的转移 都是上一层的所有 $m$ 种状态点 向下一层的所有 $m$ 种状态点连有向边,这样最多有 $2^{2m}$ 条边。这是个有环图,也就是说转移若干层(最多 $256$ 层)后,就会回到原来的一种状态。这样我们就发现有些情况的入度是 $0$,即没有任何状态能转移到它,那这些状态就是没用的,在预处理转移矩阵的时候就不放它们,对剩下的有用状态照常处理。实测 $m=8$ 时只有 $71$ 个有用状态。
T3
tag:树状数组+链上二分。
暴力的做法就是取出查询的链,然后扫两遍,求带权中位点(就是找一个位置,使两边的权值差的绝对值最小)。时间复杂度 $O(q imes n)$。
这种题显然需要数据结构维护(虽然我不是很会在树上套数据结构)。
我们可以拆出 $3$ 个部分:
1. 单点修改
2. 找出一条链上的带权中位点
3. 求链上所有点到其带权中位点的带权距离和(附加的那一堆深度……明显是等差数列,等差数列)
$2$ 操作是决策操作,所以首先考虑定死的 $1,3$ 操作能否同时完成。
有一种可以维护树上链权和的数据结构,叫树状数组。
首先单点修改可以看成减一个数再加一个数,也就是单点加。开个数组记一下每个位置上的数即可。
为了记链权和,我们在单点加时 给以修改点为根的子树的所有点都加上同样的加数。由于子树是一段连续的 $dfs$ 序区间,所以子树加的操作 用以 $dfs$ 序为下标的树状数组 随便维护就行了。
然后假设一条链的两端点为 $x,y$,$lca$ 为 $x$($y$ 同理),如图
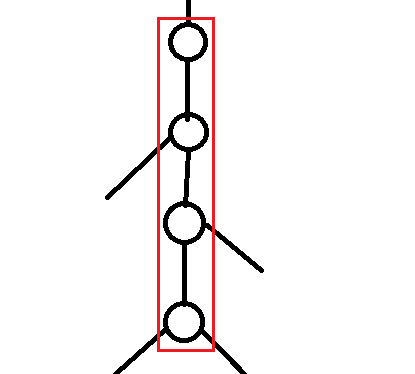
我们定义一个点的权值为从根节点到这个点的路径上所有点的 数值 $ imes$ 深度 的和,则这段链的权值和为 $T(y)-T(fa(x))$。
其中 $fa(i)$ 为点 $i$ 的父亲,$T(i)$ 为以点 $i$ 的权值,深度是指在整棵树中的深度。
其实就是普通前缀和的思想。一个点到根的路径的权值和 只会受到它所有祖先的影响,而你在更改祖先时就已经把包括这个点在内的所有子孙都更新了,所以查询的时候直接前缀相减就行了。
同时,我们还解决了区间统计时,深度的递增所带来的影响。
那么对于 求链上所有点到其带权中位点的带权距离和 这个问题,我们就可以把一条两端为点 $x,y$,$lca$ 为 $L$ 的链拆成 $3$ 条像上面一样的不拐弯的链:
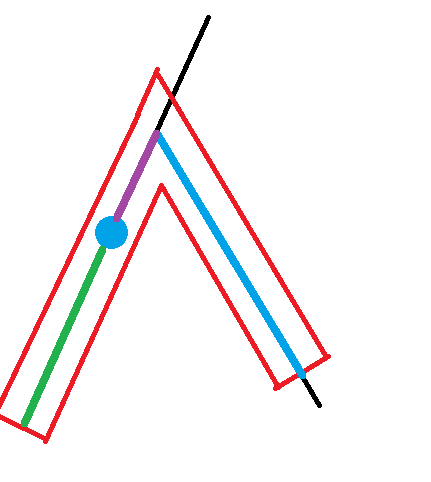
假设蓝点是中位点,其编号为 $k$,则绿色链很好处理,其贡献为 $[T(x)-T(fa(k))]-sum(k,x) imes depth(k)$,其中 $sum(k,x)$ 为 从点 $k$ 到点 $x$ 的所有点上的数的和;
蓝色链也很好处理,其贡献为 $[T(y)-T(fa(L))]-sum(L,y) imes [depth(k)-depth(L)]$;
紫色链就麻烦点,因为这部分的深度是倒过来计算的,所以贡献为 $sum(L,k) imes depth(k) - [T(k)-T(fa(L))]$。
那最后的问题就是……查询链上所有点上的数的和?
再维护一个树状数组,像维护链上的权值和一样做就行了。
然后考虑能否在此基础上再支持 $2$ 操作。
首先我们得知道找带权中位点的本质:找一个点,使得两侧的点权和的差最小(这里的差肯定要取绝对值)。
有个很暴力的做法,就是我们发现 在移动假想中位点的时候 两侧的点权和的差值变化 是个二次函数图像。
所以我们可以直接链上三分,找出差值的最小值所在处。这样的话就得快速移动假想中位点,需要用倍增或树剖。总时间复杂度是 $O(n imes log^3(n))$ 的,带上大常数,卡不过……
先不管树剖,如果我们用的是倍增,我们会发现三分和倍增移动其实是同一类东西,两者可以合并。
也就是说,可以从底部倍增往上跳,然后找到第一个两侧差值变号的位置,暴力判断它和相邻的点谁绝对差值更小就行了。
考虑到链会在 $lca$ 处打折,把链以 $lca$ 为界拆成两半,分别找这个位置,然后再取最优者就行了(其实很显然,至少有一边找到的位置是 $lca$)。
这个做法叫链上二分,但实际上只用了倍增。
然后用倍增或树状数组的方法即可单 $log$ 求链上权值和。
总时间复杂度 $O(n imes log^2(n))$。