第九章(2)、推荐系统
1.基于内容推荐content based recommendations
根据内容给产品一个度(电影的浪漫度,喜剧度,动作度)

使用线性回归方法(将除以m删掉了):

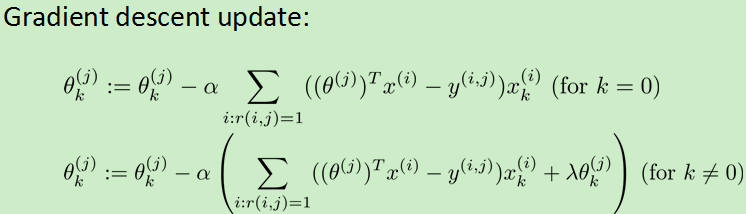
缺点:
这种方法需要根据内容给产品一个度值,很花时间,只能用于容易确定度值的问题。
反过来求:
依然使用上面的例子,现在给出每个用户的theta,不知道电影的度值,这样依然是使用线性回归方法,来最小化代价,求X。
知道了这两个算法之后的解法:
首先,随机初始化theta的值,然后求X,再用求得的X求theta,这样子不断迭代,直到代价小于一定值,或者改变幅度很小。
2.协同过滤算法(collaborative filtering)
协同过滤算法指的是:通过大量用户的评价得到大量的数据,这些用户在高效的合作,来得到每个人对于电影的评价,每个用户都在帮助算法更好的运行,并为用户提供推荐。协同的另一层意思是说每位用户都在为了大家的利益。
前面那个不断迭代的算法很慢,有一个好的算法,将两者theta和X一起当做变量来求解,新的代价函数:

X和theta都是R^n维度的,不需要增加X0和theta0。
新算法的步骤:

同样这个算法可能出现局部最值,非整体最值。
3.低秩矩阵分解Low rank matrix factorization


原式=
4.推荐产品、电影:产品特征相减选最小的。比如:

5.均值归一化Mean Normalization
如果有一个用户,它一次也没有评价电影,那么使用上述算法求得的它的theta是0,可能不能给他推荐电影
解决方法:
对于一个评价矩阵(每行表示一个电影,每列表示一个用户),求出每一行的平均值(只计算已经评价的),原矩阵的每一个元素减去对应行的均值,生成新的矩阵,用这个矩阵来做协同过滤算法,求得theta和X,然后预测函数改为 ,就是多加了对应行的均值,这样的话,没有评价的用户正好会得到每个电影的均值作为预测。如下:
,就是多加了对应行的均值,这样的话,没有评价的用户正好会得到每个电影的均值作为预测。如下:

代码:
1.代价函数
function [J, grad] = cofiCostFunc(params, Y, R, num_users, num_movies,num_features, lambda) %高级算法只能用一维的,所以要转化 X = reshape(params(1:num_movies*num_features), num_movies, num_features); Theta = reshape(params(num_movies*num_features+1:end), ... num_users, num_features); J = 0; X_grad = zeros(size(X)); Theta_grad = zeros(size(Theta)); J=sum(sum((X*(Theta')-Y).^2 .* R))/2+... sum(sum(X.*X))*lambda/2+sum(sum(Theta.*Theta))*lambda/2; X_grad=((X*(Theta')-Y).* R *Theta)+lambda*X; Theta_grad=(((X*(Theta')-Y).* R)' *X)+lambda*Theta; grad = [X_grad(:); Theta_grad(:)];%合并 end
2.均值归一化
function [Ynorm, Ymean] = normalizeRatings(Y, R) [m, n] = size(Y); Ymean = zeros(m, 1); Ynorm = zeros(size(Y)); for i = 1:m idx = find(R(i, :) == 1); Ymean(i) = mean(Y(i, idx)); Ynorm(i, idx) = Y(i, idx) - Ymean(i); end end
3.算法检验,求偏导数
function numgrad = computeNumericalGradient(J, theta) numgrad = zeros(size(theta)); perturb = zeros(size(theta)); e = 1e-4; for p = 1:numel(theta) % Set perturbation vector perturb(p) = e; loss1 = J(theta - perturb); loss2 = J(theta + perturb); % Compute Numerical Gradient numgrad(p) = (loss2 - loss1) / (2*e); perturb(p) = 0; end end
function checkCostFunction(lambda) if ~exist('lambda', 'var') || isempty(lambda) lambda = 0; end X_t = rand(4, 3); Theta_t = rand(5, 3); Y = X_t * Theta_t'; Y(rand(size(Y)) > 0.5) = 0; R = zeros(size(Y)); R(Y ~= 0) = 1; X = randn(size(X_t)); Theta = randn(size(Theta_t)); num_users = size(Y, 2); num_movies = size(Y, 1); num_features = size(Theta_t, 2); numgrad = computeNumericalGradient( ... @(t) cofiCostFunc(t, Y, R, num_users, num_movies, ... num_features, lambda), [X(:); Theta(:)]); [cost, grad] = cofiCostFunc([X(:); Theta(:)], Y, R, num_users, ... num_movies, num_features, lambda); disp([numgrad grad]); fprintf(['The above two columns you get should be very similar. ' ... '(Left-Your Numerical Gradient, Right-Analytical Gradient) ']); diff = norm(numgrad-grad)/norm(numgrad+grad); fprintf(['If your backpropagation implementation is correct, then ' ... 'the relative difference will be small (less than 1e-9). ' ... ' Relative Difference: %g '], diff); end
4.整体代码
clear ; close all; clc load ('ex8_movies.mat'); %imagesc(Y); %ylabel('Movies'); %xlabel('Users'); load ('ex8_movieParams.mat'); % Reduce the data set size so that this runs faster num_users = 4; num_movies = 5; num_features = 3; X = X(1:num_movies, 1:num_features); Theta = Theta(1:num_users, 1:num_features); Y = Y(1:num_movies, 1:num_users); R = R(1:num_movies, 1:num_users); %J = cofiCostFunc([X(:) ; Theta(:)], Y, R, num_users, num_movies, ... num_features, 1.5); checkCostFunction(1.5); clear ; close all; clc movieList = loadMovieList(); my_ratings = zeros(1682, 1); my_ratings(1) = 4; my_ratings(98) = 2; my_ratings(7) = 3; my_ratings(12)= 5; my_ratings(54) = 4; my_ratings(64)= 5; my_ratings(66)= 3; my_ratings(69) = 5; my_ratings(183) = 4; my_ratings(226) = 5; my_ratings(355)= 5; %for i = 1:length(my_ratings) % if my_ratings(i) > 0 % fprintf('Rated %d for %s ', my_ratings(i), ... % movieList{i}); % end %end load('ex8_movies.mat'); Y = [my_ratings Y]; R = [(my_ratings ~= 0) R]; [Ynorm, Ymean] = normalizeRatings(Y, R); num_users = size(Y, 2); num_movies = size(Y, 1); num_features = 10; % Set Initial Parameters (Theta, X) X = randn(num_movies, num_features); Theta = randn(num_users, num_features); initial_parameters = [X(:); Theta(:)]; options = optimset('GradObj', 'on', 'MaxIter', 100); lambda = 10; theta = fmincg (@(t)(cofiCostFunc(t, Ynorm, R, num_users, num_movies, ... num_features, lambda)), ... initial_parameters, options); X = reshape(theta(1:num_movies*num_features), num_movies, num_features); Theta = reshape(theta(num_movies*num_features+1:end), ... num_users, num_features); p = X * Theta'; my_predictions = p(:,1) + Ymean; movieList = loadMovieList(); [r, ix] = sort(my_predictions, 'descend'); for i=1:10 j = ix(i); fprintf('Predicting rating %.1f for movie %s ', my_predictions(j), ... movieList{j}); end for i = 1:length(my_ratings) if my_ratings(i) > 0 fprintf('Rated %d for %s ', my_ratings(i), ... movieList{i}); end end