同余
基本定理
欧拉定理
若a,m互质，则
[a^{varphileft ( m
ight )}equiv 1left ( mod m
ight )
]
应用
令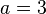
，
，这两个数是互素的。比5小的正整数中与5互素的数有1、2、3和4，所以
。计算：
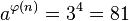，而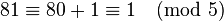
。与定理结果相符。
计算
的个位数，实际是求被10除的余数。7和10互素，且
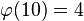。由欧拉定理知
。所以
。
费马小定理
若p是质数，则对于任意整数a，都有
[a^{p}equiv aleft ( mod p
ight )
]
扩展欧拉定理
[a^{b} mod m,若 b>=varphileft ( m
ight ),则
]
[a^{b} equiv a^{b mod varphi left ( m
ight )+varphileft ( m
ight )}left ( mod m
ight )
]
扩展欧几里得算法
搬到另一篇博客：