求最大密度子图方案。密度=边数/点数
假设E,V为最大密度子图的边数点数。则$forall ho$有$ ho leqslant frac{E}{V}$即$E- ho V geqslant 0$,也就是说密度最大时不等式去等号,密度要是小一些的话就应大于0,那可以二分密度寻找最大的密度,判断是否合法的方法:要看左边的等式有没有大于0,那可以把点看成权值是$- ho$的点,边抽象成权值为$1$的点,且其向连接两端的点连有向边。然后做最大权闭合子图,保证边选上就得把点也给选上。这样得到的最大权大于零说明密度枚举小了,而为零表示枚举值大于等于最大密度。那就通过二分找到那个刚好突变的数就是最大密度,这是停止二分把残量网络跑一遍,得所选点。
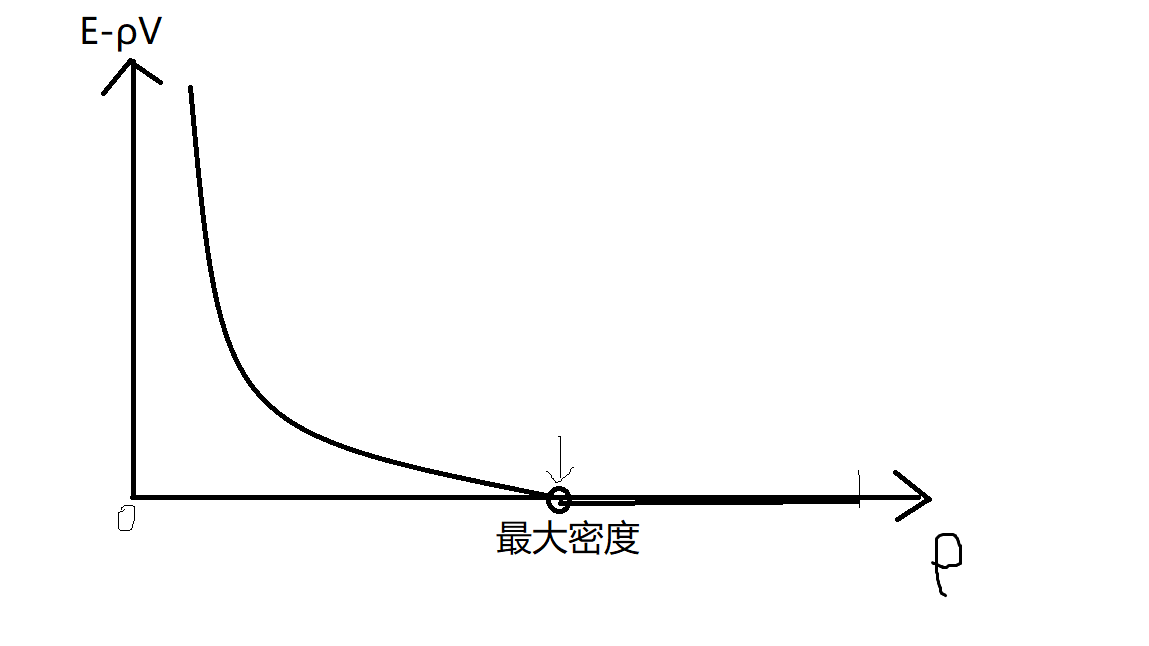
这题稍微卡精度,还是说我不太会写浮点数二分答案?很玄学。
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<queue> 5 #include<cmath> 6 using namespace std; 7 typedef long long ll; 8 typedef double db; 9 #define dbg(x) cerr<<#x<<" = "<<x<<endl 10 template<typename T>inline char MIN(T&A,T B){return A>B?A=B,1:0;} 11 template<typename T>inline char MAX(T&A,T B){return A<B?A=B,1:0;} 12 template<typename T>inline T _min(T A,T B){return A<B?A:B;} 13 template<typename T>inline T _max(T A,T B){return A>B?A:B;} 14 template<typename T>inline void inc(T&A,T B){A+=B;} 15 inline int read(int&x){ 16 x=0;int f=0;char c;while(!isdigit(c=getchar()))if(c=='-')f=1; 17 while(isdigit(c))x=x*10+c-'0',c=getchar();if(c==' ')return -1;return f?-x:x; 18 } 19 const int N=1100+9,M=3200+7;const db eps=1e-5,INF=99999999.0; 20 int Head[N],cur[N],Next[M<<1],v[M<<1],dis[N],vis[N],tot,n,m,s,t; 21 db w[M<<1]; 22 inline void Addedge(int x,int y,db z){ 23 v[++tot]=y,Next[tot]=Head[x],Head[x]=tot,w[tot]=z; 24 v[++tot]=x,Next[tot]=Head[y],Head[y]=tot,w[tot]=0; 25 } 26 #define y v[j] 27 inline int bfs(){ 28 queue<int> q;memset(dis,0,sizeof dis),dis[s]=1,q.push(s); 29 for(register int i=1;i<=(n+m)+2;++i)cur[i]=Head[i]; 30 while(!q.empty()){ 31 int x=q.front();q.pop(); 32 for(register int j=Head[x];j;j=Next[j])if(w[j]>0&&!dis[y]){ 33 dis[y]=dis[x]+1,q.push(y); 34 if(y==t)return 1; 35 } 36 } 37 return 0; 38 } 39 db dinic(int x,db flow){ 40 if(flow<eps||x==t)return flow; 41 db rest=flow,k; 42 for(register int j=cur[x];j&&rest;cur[x]=j,j=Next[j])if(w[j]>0&&dis[y]==dis[x]+1){ 43 if((k=dinic(y,_min(rest,w[j])))<eps)dis[y]=0; 44 rest-=k,w[j]-=k,w[j^1]+=k; 45 } 46 return flow-rest; 47 } 48 #undef y 49 int flag,edge[1005][2],cnt; 50 db L,R,mid,res,maxflow,ans; 51 52 inline db check(db rho){//dbg(rho); 53 memset(Head,0,sizeof Head);maxflow=ans=0;tot=1; 54 for(register int i=1;i<=m;++i)ans+=1.0,Addedge(s,i,1.0),Addedge(i,edge[i][0]+m,INF),Addedge(i,edge[i][1]+m,INF); 55 for(register int i=1;i<=n;++i)Addedge(i+m,t,rho); 56 while(bfs())maxflow+=dinic(s,INF); 57 ans-=maxflow;//dbg(maxflow);dbg(ans); 58 return ans; 59 } 60 void dfs(int x){//cerr<<x<<endl; 61 vis[x]=1;for(register int j=Head[x];j;j=Next[j]){ 62 // dbg(v[j]),dbg(w[j]); 63 if(w[j]>0&&!vis[v[j]])dfs(v[j]); 64 } 65 } 66 67 int main(){//freopen("tmp.in","r",stdin);//freopen("tmp.out","w",stdout); 68 while(~scanf("%d%d",&n,&m)){ 69 if(flag)puts("");else flag=1; 70 if(m==0){printf("1 1 ");continue;} 71 for(register int i=1;i<=m;++i)read(edge[i][0]),read(edge[i][1]); 72 L=0,R=m/2.0;s=n+m+1,t=s+1; 73 while(R-L>eps){//dbg(L),dbg(R); 74 mid=(L+R)/2.0;db res=check(mid); 75 if(res<eps)R=mid-eps; 76 else L=mid; 77 } 78 check(L),memset(vis,0,sizeof vis),dfs(s);cnt=0; 79 for(register int i=1;i<=n;++i)if(vis[i+m])++cnt; 80 printf("%d ",cnt); 81 for(register int i=1;i<=n;++i)if(vis[i+m])printf("%d ",i); 82 } 83 return 0; 84 }