甚至有时候都算不上开始,因为功能有实效要求。
最近面试总是遇到,理直气壮的认为实现了就行了,于是我整理了下大学数据结构的部分内容。
主要是关于斐波那契数列的计算方法。斐波那契数列就不介绍了,大概就是这样的:fib(n) = fib(n - 1) + fib(n - 2)。
用递归可以很容易实现:

然而,这里n只设为了5,如果设置的比较大,会发现递归到40多项时已经无法忍受计算速度了,现在用数据结构里学过的时间复杂度分析:
复杂度:T(n) = T(n - 1) + T(n - 2) + 1,用T(n - 1) 和 T(n - 2) 的时间算出T的前两项以及O(1)时间相加,因为T(0)和T(1)的时间复杂度都是1,当n > 1时,可使用s(n) = [T(n) + 1]/2求解,对边界条件s(0) = 1,s(1) = 1,碰巧等于斐波那契数列的前两项。其实也并不是碰巧,s(n) = s(n - 1) + s(n - 2)其实就等于fib(n + 1),复杂度大致为O(Φ的n次方),(Φ=二分之(一加根号5)约等于1+黄金分割比例),T(n)约等于2*s(n),时间复杂度也呈斐波那契数列变化,量级O(Φ的n次方)大致为O(2的n次方),数值上Φ的36(6的平方)次方=2的25(5的平方)次方,Φ的43次方=2的30次方=2的10次方的3次方约等于10的9次方,10的9次方是目前主流计算机大概1秒的指令吞吐量,Φ的5次方Φ**5 = 10,Φ**67约等于10**14约执行10**5秒,大概是1天,Φ**92 : 10**19 : 10**10秒 :10**5天 : 3个世纪。也就是说要算出第67项,这个算法需要1天时间,而第92项需要三个世纪。
那么,为什么这么慢呢。其实可以从上面的代码的输出中看出原因:
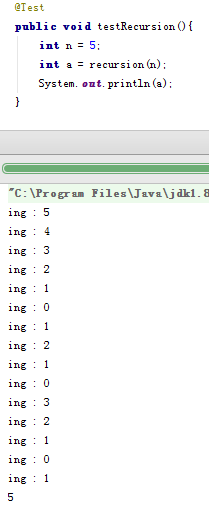
这个递归中存在大量的重复计算,因为子项的计算包含子项的子项,而其他子项可能已经计算过这个步骤了,但是它不得不又算了一次从这个角度来看,最简单的解决办法就是记录所有计算过的子项,先查找,没有的话再计算,这种方式的缺点是用空间复杂度比较高。
还可以有时间复杂度和空间复杂度都比较低的方法,动态规划,在代码上也就是嵌套改循环:

92项用了不到一毫秒,注意,这里n--,实际上等于计算的是之前的方法的93项。
虽然现在大家都接受了能用硬件增加的性能不要用程序员解决,但是实际上你即使用天河一号算递归的方法也不会比普通PC算循环的方法快,而且用硬件解决并不是说就不需要注意算法了。
最后,摘抄了一段关于动态规划的内容,忘了当初从哪记得下来的了,所以没有出处,以上。
能采用动态规划求解的问题的一般要具有3个性质:
(1) 最优化原理:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
(2) 无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
(3)有重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势
以上测试代码在:https://github.com/saaavsaaa/warn-report/blob/master/src/test/java/structure/FibonacciTest.java
testDyPro和testRecursion方法
以上内容参考清华大学邓俊辉教授的数据结构视频课程
==========================================================
咱最近用的github:https://github.com/saaavsaaa
微信公众号:

转载请注明出处