今天上午某学长讲了一上午的网络流w表示有点迷糊
紧接着老于就立了"联赛不考网络流"的flag
虽然依然不大会用但是挖个坑先写着(逃
==== €€£ WARNING ====
这篇博文由于过于久远再加上博主当时比较naive所以并没有多少内容, 已经被废弃
大量扩充版本: [教程]网络流详解: 从入门到放弃
==== ====
1.定义
假设 $G = (V,E)$ 是一个有限的有向图,它的每条边 $(u,v) in E$ 都有一个非负值实数的容量$ c(u, v)$。如果$ (u, v) ot in E$,我们假设$ c(u, v) = 0$。我们区别两个顶点:一个源点 $s$ 和一个汇点$ t$。一道网络流是一个对于所有结点$ u$ 和$ v $都有以下特性的实数函数$ f:V imes V ightarrow mathbb{R}$:
容量限制(Capacity Constraints):$ f(u, v) leq c(u, v)$一条边的流不能超过它的容量。
斜对称(Skew Symmetry):$ f(u, v) = - f(v, u)$由 $u$到 $v$的净流必须是由 $v$到 $u$的净流的相反(参考例子)。
流守恒(Flow Conservation): 除非 $u = s$或 $u = t$,否则 $sum_{w in V} f(u, w) = 0$一结点的净流是零,除了“制造”流的源点和“消耗”流的汇点。
即流守恒意味着:$ sum_{(u,v) in E} f(u,v) = sum_{(v,z) in E} f(v,z)$ ,对每个顶点$ v in Vsetminus{s,t}$
注意$ f(u,v)$ 是由 $u$ 到 $v $的净流。如果该图代表一个实质的网络,由$ u $到$ v $有4单位的实际流及由$ v$ 到 $u $有3单位的实际流,那么 $f(u, v) = 1 $及 $f(v, u) = -1$。
基本上,我们可以说,物理网络的网络流是从$ s = sum_{(s,v)in E} f(s,v) $出发的流
边的剩余容量(residual capacity)是$ c_f(u, v) = c(u, v) - f(u, v)$。这定义了以 $G_f(V, E_f) $表示的剩余网络(residual network),它显示可用的容量的多少。留意就算在原网络中由 $u$ 到 $v $没有边,在剩余网络仍可能有由$ u $到$ v $的边。因为相反方向的流抵消,减少由 $v $到$ u$ 的流等于增加由$ u$ 到 $v $的流。增广路(augmenting path)是一条路径$ (u_1, u_2, dots, u_k)$,而 $u_1 = s$、$ u_k = t $及 $c_f(u_i, u_{i+1}) > 0$,这表示沿这条路径发送更多流是可能的。当且仅当剩余网络$ G_f $没有增广路时处于最大流。
因此如下使用图 $G$ 创建 $ G_f $:
$G_f = V $的顶点
定义如下的 $G_f = E_f $的边
对每条边$ (x,y) in E$
若$ f(x,y) < c(x,y)$,创建容量为$ c_f = c(x,y) - f(x,y)$ 的前向边 $(x,y) in E_f$。
若$ f(x,y) > 0$,创建容量为$ c_f = f(x,y) $的后向边 $(y, x) in E_f$。
这个概念用在计算流量网的最大流的Ford–Fulkerson算法中。
有时需要对有多于一个源点的网络,于是就引入了图的超源点。这包含了一个与无限容量的边连接的每个源点,以作为一个整体源点。汇点也有类似的构造称作超汇点。
以上是摘自Wikipedia的定义
2.最大流算法
常见的最大流(Max-Flow)算法有如下几种:
$O(VE^2)$的Edmonds–Karp算法;$O(V^2E)$的Dinic阻塞流算法.最大流问题的渐近时间复杂度最低的算法是$O(VE)$的James B Orlin's + KRT (King, Rao, Tarjan)算法,但是似乎要用到手写Fibonacci heap所以实用度不高.
3.增广路
增广路的定义在定义中已经一同交代,许多最大流算法的中心思想就是不断寻找增广路来扩充流,当残存网络中没有增广路时获得最大流.
但是实际上我们在网络流的定义中会看到有前向边和后向边,这些方向相反的边的意义在于防止无法对已经找到的流方案进行修改从而得不到最大流的情况.比如:
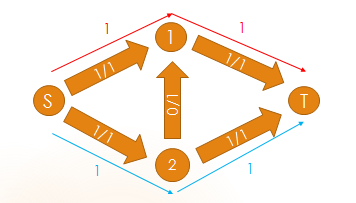
对于这个流网络,图示为最大流,但是当我们寻找增广路时不幸遇到了这种情况:
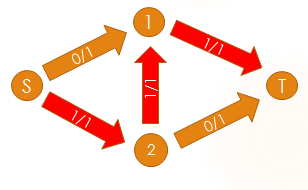
则算法会无法继续找到新的增广路并退出.这时通过反向边可以给以后的增广路查找留下更改流方案的机会.
4.EdmondsKarp算法
EK算法通过多次BFS查找增广路,思想还算明确.时间复杂度$O(VE^2)$
表示还是Dinic大法好所以直接粘课件里的板子了233

1 int Bfs() { 2 memset(pre, -1, sizeof(pre)); 3 for(int i = 1 ; i <= n ; ++ i) flow[i] = INF; 4 queue <int> q; 5 pre[S] = 0, q.push(S); 6 while(!q.empty()) { 7 int op = q.front(); q.pop(); 8 for(int i = 1 ; i <= n ; ++ i) { 9 if(i==S||pre[i]!=-1||c[op][i]==0) continue; 10 pre[i] = op; //找到未遍历过的点 11 flow[i] = min(flow[op], c[op][i]); // 更行路径上的最小值 12 q.push(i); 13 } 14 } 15 if(flow[T]==INF) return -1; 16 return flow[T]; 17 } 18 int Solve() { 19 int ans = 0; 20 while(true) { 21 int k = Bfs(); 22 if(k==-1) break; 23 ans += k; 24 int nw = T; 25 while(nw!=S) {//更新残余网络 26 c[pre[nw]][nw] -= k, c[nw][pre[nw]] += k; 27 nw = pre[nw]; 28 } 29 } 30 return ans; 31 }
5.Dinic阻塞流算法
Dinic算法首先通过BFS来建立层次图(其实就是求深度233),然后在层次图中跑DFS直到没有增广路,然后重复上述两步直至BFS无法到达汇点$t$.理论时间复杂度$O(V^2E)$.
看起来时间复杂度很高但是实际跑得飞起,时间复杂度O(能过)

1 int Dinic(int s,int t){ 2 int ans=0; 3 while(BFS(s,t)){ 4 ans+=DFS(s,INF,t); 5 } 6 return ans; 7 } 8 9 int DFS(int s,int flow,int t){ 10 if(s==t||flow==0) 11 return flow; 12 int tmp=flow; 13 int k; 14 for(Edge* i=head[s];i!=NULL;i=i->next){ 15 if(i->flow!=0&&tmp!=0&&depth[i->to]==depth[s]+1){ 16 k=DFS(i->to,std::min(tmp,i->flow),t); 17 if(k==0){ 18 depth[i->to]=0; 19 continue; 20 } 21 tmp-=k; 22 i->flow-=k; 23 i->rev->flow+=k; 24 if(tmp==0) 25 break; 26 } 27 } 28 return flow-tmp; 29 } 30 31 bool BFS(int s,int t){ 32 memset(depth,0,sizeof(depth)); 33 std::queue<int> q; 34 depth[s]=1; 35 q.push(s); 36 while(!q.empty()){ 37 s=q.front(); 38 q.pop(); 39 for(Edge* i=head[s];i!=NULL;i=i->next){ 40 if(depth[i->to]==0&&i->flow!=0){ 41 q.push(i->to); 42 depth[i->to]=depth[s]+1; 43 if(i->to==t) 44 return true; 45 } 46 } 47 } 48 return false; 49 }
6.最大流与最小割
有了最大流算法之后题目难点就在于如何建图来跑网络流.这里先列一个题表挖坑,题解慢慢补qwq
COGS_0014 BZOJ_1458 BZOJ_1189 COGS_2051 BZOJ_2127 BZOJ_2039 BZOJ_3144 BZOJ_1797
7.费用流
费用流最常用的也就是最小费用最大流了w
这时候我们只需寻找增广路时采取最短增广路的贪心策略即可.反向边的边权为正向边的相反数.由于会存在负权所以只能选择SPFA这种玄学的东西(玄学套玄学...可能这就是OI吧)
列个题表回来填坑...
COGS_0461 BZOJ_1449 BZOJ_2597
补图

