一、
P01: 01背包问题
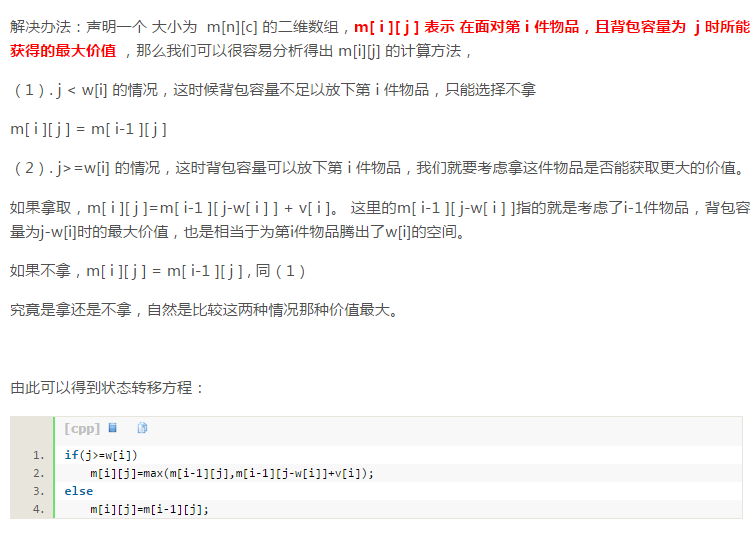
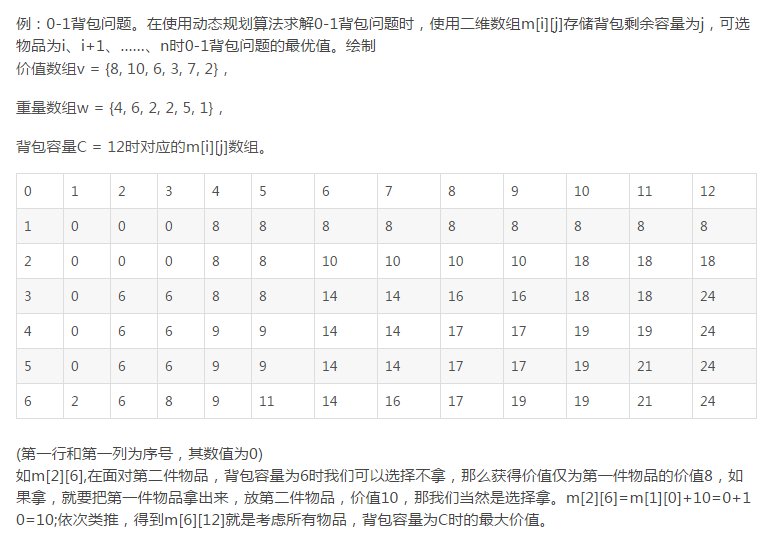
N件物品和一个容量为V 的背包。放入第i件物品耗费的费用是Ci1,得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。
价值数组v = {8, 10, 6, 3, 7, 2},
重量数组w = {4, 6, 2, 2, 5, 1},
背包容量C = 12。不超过容量的情况下,使得价值最大。
1、
#include<iostream>
#include<string.h>
#include<cmath>
using namespace std;
int main()
{
int v[7]={0,8,10,6,3,7,2};//价值 ,一定要注意对应关系,多一行,多一列
int w[7]={0,4,6,2,2,5,1};//重量
int c=12,n=6;//容量,个数
int num[6+1][12+1]={0};//预留空间多了一行和一列
for(int i=1;i<=n;i++) //num[i][j],i个物品,j为容量时,的最大价值
{
for(int j=1;j<=c;j++)
{
if(w[i]<=j)//可以选择 ,比较新加的和旧的哪个大
{
num[i][j]=max(num[i-1][j],num[i-1][j-w[i]]+v[i]);
}
else//重量比容量大,不被选择,维持原来
{
num[i][j]=num[i-1][j];
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<num[i][j]<<" ";
}
cout<<endl;
}
}
一定要注意空间的声明,可以提前声明一个较大的空间这样避免空间溢出。
以上是矩阵所有数据都保存下来,可以只保存两行c列,优化空间
2、
#include<iostream>
#include<string.h>
#include<cmath>
using namespace std;
int main()
{
int v[7]={0,8,10,6,3,7,2};//价值 ,一定要注意对应关系,多一行,多一列
int w[7]={0,4,6,2,2,5,1};//重量
int c=12,n=6;//容量,个数
int num[12+1]={0};//预留空间多了一行和一列
int tem[12+1]={0};//中间变量
for(int i=1;i<=n;i++) //num[i][j],i个物品,j为容量时,的最大价值
{
for(int j=1;j<=c;j++)
{
if(w[i]<=j)//可以选择 ,比较新加的和旧的哪个大
{
num[j]=max(tem[j],tem[j-w[i]]+v[i]);
}
else//重量比容量大,不被选择,维持原来
{
num[j]=tem[j];
}
}
for(int k=0;k<13;k++)
{
tem[k]=num[k];
}
}
for(int i=1;i<13;i++)
{
cout<<num[i]<<" ";
}
}

大大节省空间。
3、只保留一行的逆序求解程序;
#include<iostream>
#include<string.h>
#include<cmath>
using namespace std;
int main()
{
int v[7]={0,8,10,6,3,7,2};//价值 ,一定要注意对应关系,多一行,多一列
int w[7]={0,4,6,2,2,5,1};//重量
int c=12,n=6;//容量,个数
int num[12+1]={0};//预留空间多了一列 存储0位置
for(int i=1;i<=n;i++) //num[i][j],i个物品,j为容量时,的最大价值
{
for(int j=c;j>0;j--)//因为需要用到前面的数据,所以逆向求解
{
if(w[i]<=j)//可以选择 ,比较新加的和旧的哪个大
{
num[j]=max(num[j],num[j-w[i]]+v[i]);
}
}
}
for(int i=1;i<13;i++)
{
cout<<num[i]<<" ";
}
}

4、利用递归的方法求解
#include<iostream>
#include<string.h>
#include<cmath>
using namespace std;
int Getnum(int n,int c)
{
int v[7]={0,8,10,6,3,7,2};//价值 ,一定要注意对应关系,多一行,多一列
int w[7]={0,4,6,2,2,5,1};//重量
int num=0;
if(n==0)//边界条件
num=0;
else
{
if(c<w[n])
{
num=Getnum(n-1,c);
}
else
{
num=max(Getnum(n-1,c),Getnum(n-1,c-w[n])+v[n]);
}
}
return num;
}
int main()
{
int c=12,n=6;//容量,个数
cout<<Getnum(6,12);
}
利用这样的方法,程序简单,但是会增加时间复杂度。
5、将该问题改为循环输入
#include<iostream>
#include<string.h>
#include<cmath>
using namespace std;
const int N=50;
int v[N]={0};
int w[N]={0};
int Getnum(int n,int c)
{
//int v[6]={8,10,6,3,7,2};//价值 ,一定要注意对应关系,多一行,多一列
//int w[6]={4,6,2,2,5,1};//重量
int num=0;
if(n==0)//边界条件
num=0;
else
{
if(c<w[n])
{
num=Getnum(n-1,c);
}
else
{
num=max(Getnum(n-1,c),Getnum(n-1,c-w[n])+v[n]);
}
}
return num;
}
int main()
{
int c,n;//容量,个数
while(cin>>c>>n)
{
for(int i=1;i<=n;i++)
{
cin>>v[i];
}
for(int i=1;i<=n;i++)
{
cin>>w[i];
}
cout<<Getnum(n,c);
v[N]={0};
w[N]={0};
}
}
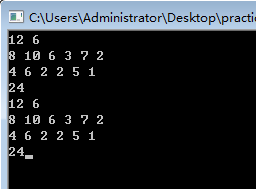
6、
通过指针来传递数组
#include<iostream>
#include<cmath>
#include<string.h>
using namespace std;
int Sum(int n,int *P)//指针来传递数组
{
int s;
for(int i=0;i<n;i++)
{
s+=P[i];
}
return s;
}
int main()
{
int v[5]={0,1,2,3,4};
cout<<Sum(5,v);
}

二、
P02: 完全背包问题
题目
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
/*"""
完全背包问题(每个物品可以取无限次)
:param N: 物品个数, 如 N=5
:param V: 背包总容量, 如V=15
:param weight: 每个物品的容量数组表示, 如weight=[5,4,7,2,6]
:param value: 每个物品的价值数组表示, 如value=[12,3,10,3,6]
:return: 返回最大的总价值
"""*/
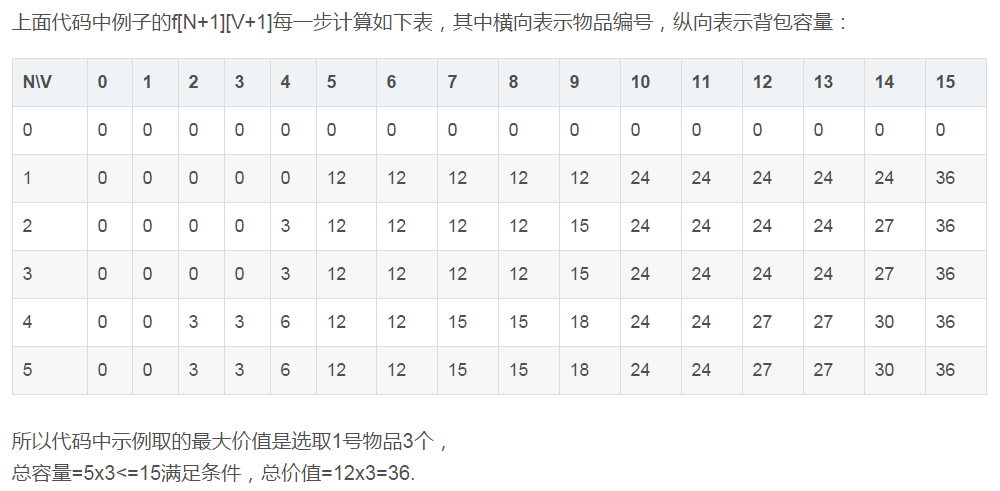
代码实现
1、
#include <iostream>
#include <cstring>
using namespace std;
const int N=50;
int main()
{
int v[N]={0,12,3,10,3,6};//价值
int w[N]={0,5,4,7,2,6}; //重量
int m[N][N];
int n=5,c=15; //容量15
memset(m,0,sizeof(m));
cout<<m[2][0]<<endl;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
m[i][j]=m[i-1][j];
for(int k=1;k<=(j/w[i]);k++)
{
if(m[i-1][j]<m[i-1][j-w[i]*k]+v[i]*k)
m[i][j]=m[i-1][j-w[i]*k]+v[i]*k;
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
return 0;
}

多次循环比较要比的不仅仅是 m[i-1][j]和m[i-1][j-w[i]*k]+v[i]*k单一的一个数比较。随着k的变化,其实是m[i-1][j]、m[i-1][j-w[i]*k]+v[i]*k和新生成的m[i][j]三个数的比较。写成如下形式的话就会出错
#include <iostream>
#include <cstring>
#include<cmath>
using namespace std;
const int N=50;
int main()
{
int v[N]={0,12,3,10,3,6};//价值
int w[N]={0,5,4,7,2,6}; //重量
int m[N][N];
int n=5,c=15; //容量15
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
for(int k=1;k<=(j/w[i]);k++)
{
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]*k]+v[i]*k);//出错,只比较了两个数
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
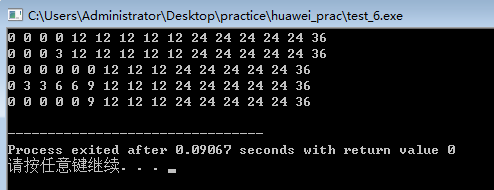
以m[2][9]为例,本应该是15,这里出现12是由于,当k=2时,m[i-1][j-w[i]*k]+v[i]*k=m[1][1]+3*2=6,小于m[i-1][j]=12,覆盖掉了之前的15。这就是由于比较没有考虑新生成的数引起的错误。
但其实上面的代码也没有与新生成的m[i][j]作比较。这是少了覆盖这一层,结果便正确~
改为如下也对
#include <iostream>
#include <cstring>
#include<cmath>
using namespace std;
const int N=50;
int main()
{
int v[N]={0,12,3,10,3,6};//价值
int w[N]={0,5,4,7,2,6}; //重量
int m[N][N];
int n=5,c=15; //容量15
memset(m,0,sizeof(m));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
m[i][j]=m[i-1][j];//相当于m[i][j]提前赋了个最大值,然后和自身比较找出最大的即可
for(int k=1;k<=(j/w[i]);k++)
{
m[i][j]=max(m[i][j],m[i-1][j-w[i]*k]+v[i]*k);//
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=c;j++)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
return 0;
}
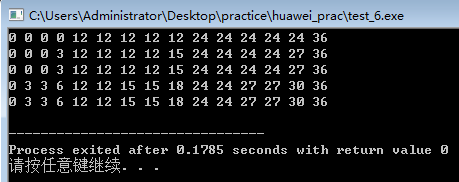
以上方法是将完全背包转换为了01背包,比较状态是n个物品和n-1个物品状态比较,
2、空间的优化
#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
int w[300],c[300],f[300010]={0};
int V,n;
int main()
{
V=15;
n=5;
int w[6]={0,12,3,10,3,6};//价值
int c[6]={0,5,4,7,2,6}; //重量
for(int i=1;i<=n;i++)
{
for(int j=c[i];j<=V;j++)//保证j>c[i]
{
f[j]=max(f[j-c[i]]+w[i],f[j]);//设 f[v]表示重量不超过v公斤的最大价值,最简单的方式
}
}
for(int i=1;i<=15;i++)
cout<<f[i]<<" ";
return 0;
}
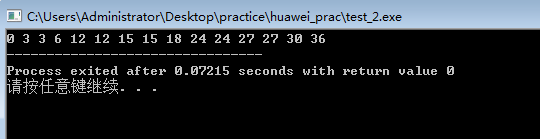
最简单的形式,判断条件和01背包相比,采用顺序,而非逆序,因为比较的是同一件物品从1加到n件的不同,而不跨越到上一个物品,而和上一个物品比较则根据下标来比的,简化了好多。
3、递归实现
#include<iostream>
#include<string.h>
using namespace std;
const int N=6;
int v[N]={0,12,3,10,3,6};//价值
int w[N]={0,5,4,7,2,6}; //重量
int dp(int n,int m)//n物品个数,m背包容量
{
int Max;
if(n==0)
return 0;
Max=dp(n-1,m);
for(int i=1;i<=m/w[n];i++)
{
Max=max(Max,dp(n-1,m-w[n]*i)+v[n]*i);//三个比较求出最大值,注意下标比较多,区分开来
}
return Max;
}
int main()
{
int n=dp(5,15);
cout<<n;
}
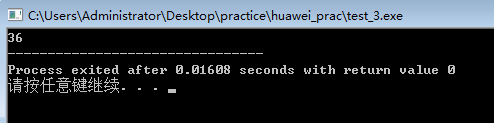
三、
P03: 多重背包问题
题目
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。


1、将多重背包转化为完全背包,只是将不确定的个数取n和c/w[i]的最小值,其他不变;
#include<iostream>
#include<cmath>
using namespace std;
int Num[100][100]={0};
int main()
{
int n=3,c=8;
int w[4]={0,1,2,2};
int v[4]={0,6,10,20};
int N[4]={0,10,5,2};
for(int i=1;i<=n;i++) //确定矩阵
{
for(int j=1;j<=c;j++)
{
int d=min(j/w[i],N[i]);
for(int k=1;k<=d;k++)
{
Num[i][j]=max(Num[i-1][j],Num[i-1][j-k*w[i]]+k*v[i]);
}
}
}
for(int j=1;j<=n;j++)
{
for(int i=1;i<=c;i++)
{
cout<<Num[j][i]<<" ";
}
cout<<endl;
}
int t[4]={0};//确定每种物品个数
int s=c;//价值总数
for(int i=n;i>0;i--)
{
int d=min(c/w[i],N[i]);
for(int k=d;k>0;k--)
{
if(Num[i][s]==(Num[i-1][s-k*w[i]]+k*v[i]))//找出最大的加的数是什么,进而求出个数
{
t[i]=k;
s=s-k*w[i];
break;
}
}
}
for(int i=1;i<=n;i++)
cout<<t[i]<<" ";
cout<<endl;
}
//3 8 1 6 10 2 10 5 2 20 2
/*3 8 //3件物品,背包承重最大为8
1 6 10 //第一件物品, 重量为1,价值为6, 数目为10
2 10 5
2 20 2*/
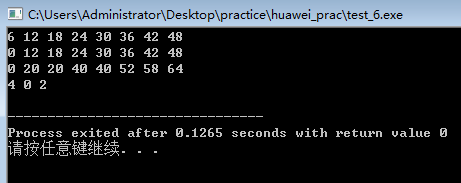
求矩阵是转化为了完全背包,只是改了个数。
求每种物品具体用的个数本想着计算的过程中就得出,但是由于只有到运算最后才能得出最大的值,所以过程中并不好判断,只能先求出矩阵后再计算。
计算过程如下:64=24+2*20;所以三好物品用了两个;24=4*6;所以一号物品用了4个,求出。
2、改进空间复杂度
没找到和想出简单易于理解的程序。
3、
#include <iostream>
using namespace std;
int knapsack_limitnum(int *W, int *V, int *N, int *res, int n, int C)
{
int value = 0;
int **f = new int*[n];
for(int i = 0; i < n; i++)
{
f[i] = new int[C+1];
}
for(int i = 0; i < n; i++)
for(int j = 0; j < C+1; j++)
f[i][j] = 0;
for(int y = 1; y < C+1; y++)
{
int count = min(N[0], y/W[0]);
f[0][y] = (y < W[0])?0:(count * V[0]);
}
for(int i = 1; i < n; i++)
{
for(int y = 1; y < C+1; y++)
{
if(y < W[i])
{
f[i][y] = f[i-1][y];
} else {
int count = min(N[i], y/W[i]);
f[i][y] = f[i-1][y];
for(int k = 1; k <= count; k++)
{
int temp = f[i-1][y-W[i]*k] + k*V[i];
if(temp >= f[i][y])
f[i][y] = temp;
}
}
}
}
for(int i = 0; i < n; i++)
{
for(int y = 0; y < C+1; y++)
cout << f[i][y] << " ";
cout << endl;
}
value = f[n-1][C];
int j = n-1;
int y = C;
while(j)
{
int count = min(N[j], y/W[j]);
for(int k = count; k > 0; k--)
{
if(f[j][y] == (f[j-1][y-W[j]*k]+k*V[j]))
{
res[j] = k;
y = y - k*W[j];
break;
}
}
j--;
}
res[0] = f[0][y]/V[0];
for(int i = 0;i < n; i++)
{
delete f[i];
f[i] = 0;
}
delete [] f;
f = 0;
return value;
}
void test1()
{
int n, C;
while(cin >> n >> C) //n:物品个数,C:承重量
{
int *W = new int[n];
int *V = new int[n];
int *N = new int[n];
int *res = new int[n];
for(int i =0; i < n; i++)
res[i] = 0; //每种物品存放的个数
int w, v, n1, i = 0;
while(i < n) //循环输入
{
cin >> w >> v >> n1;
W[i] = w; //重量
V[i] = v; //价值
N[i] = n1; //数目
i++;
}
int value = knapsack_limitnum(W, V, N, res, n, C);
cout << value << endl;//最大值
for(int i = 0; i < n; i++)
cout << res[i] << " ";//个数
cout << endl;
delete res; //res = 0; //释放空间
delete N; //N = 0;
delete V; //V = 0;
delete W; //W = 0;
}
}
int main()
{
test1();
return 0;
}
//3 8 1 6 10 2 10 5 2 20 2
/*3 8 //3件物品,背包承重最大为8
1 6 10 //第一件物品, 重量为1,价值为6, 数目为10
2 10 5
2 20 2*/
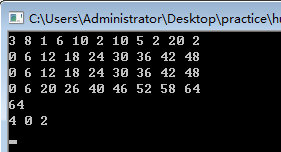
4、
自己编写循环输入和函数调用输出的整个程序。
(1)
#include<iostream>
#include<cmath>
using namespace std;
int Num[100][100]={0};
int w[100]={0},v[100]={0},N[100]={0};
int main()
{
//int n=3,c=8;
//int w[4]={0,1,2,2};
//int v[4]={0,6,10,20};
//int N[4]={0,10,5,2};
int n,c;
while(cin>>n>>c)
{
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>N[i];
}
for(int i=1;i<=n;i++) //确定矩阵
{
for(int j=1;j<=c;j++)
{
int d=min(j/w[i],N[i]);
for(int k=1;k<=d;k++)
{
Num[i][j]=max(Num[i-1][j],Num[i-1][j-k*w[i]]+k*v[i]);
}
}
}
for(int j=1;j<=n;j++)
{
for(int i=1;i<=c;i++)
{
cout<<Num[j][i]<<" ";
}
cout<<endl;
}
int t[4]={0};//确定每种物品个数
int s=c;//价值总数
for(int i=n;i>0;i--)
{
int d=min(c/w[i],N[i]);
for(int k=d;k>0;k--)
{
if(Num[i][s]==(Num[i-1][s-k*w[i]]+k*v[i]))//找出最大的加的数是什么,进而求出个数
{
t[i]=k;
s=s-k*w[i];
break;
}
}
}
for(int i=1;i<=n;i++)
cout<<t[i]<<" ";
cout<<endl;
Num[100][100]={0};
w[100]={0};v[100]={0};N[100]={0};
}
return 0;
}
//3 8 1 6 10 2 10 5 2 20 2
/*3 8 //3件物品,背包承重最大为8
1 6 10 //第一件物品, 重量为1,价值为6, 数目为10
2 10 5
2 20 2*/
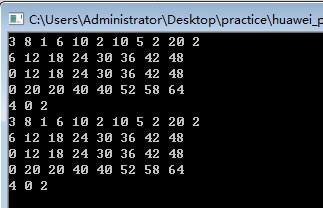
这是采用声明全局变量方法做的,也没有调用函数
(2)
#include<iostream>
#include<cmath>
using namespace std;
int Num[100][100]={0};
int w[100]={0},v[100]={0},N[100]={0};
void dp(int *w,int *v,int *N,int n,int c)//注意矩阵地址的引用
{
for(int i=1;i<=n;i++) //确定矩阵
{
for(int j=1;j<=c;j++)
{
int d=min(j/w[i],N[i]);
for(int k=1;k<=d;k++)
{
Num[i][j]=max(Num[i-1][j],Num[i-1][j-k*w[i]]+k*v[i]);
}
}
}
for(int j=1;j<=n;j++)
{
for(int i=1;i<=c;i++)
{
cout<<Num[j][i]<<" ";
}
cout<<endl;
}
int t[4]={0};//确定每种物品个数
int s=c;//价值总数
for(int i=n;i>0;i--)
{
int d=min(c/w[i],N[i]);
for(int k=d;k>0;k--)
{
if(Num[i][s]==(Num[i-1][s-k*w[i]]+k*v[i]))//找出最大的加的数是什么,进而求出个数
{
t[i]=k;
s=s-k*w[i];
break;
}
}
}
for(int i=1;i<=n;i++)
cout<<t[i]<<" ";
cout<<endl;
}
int main()
{
//int n=3,c=8;
//int w[4]={0,1,2,2};
//int v[4]={0,6,10,20};
//int N[4]={0,10,5,2};
int n,c;
while(cin>>n>>c)
{
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i]>>N[i];
}
dp(w,v,N,n,c);
Num[100][100]={0};
w[100]={0};v[100]={0};N[100]={0};
}
return 0;
}
//3 8 1 6 10 2 10 5 2 20 2
/*3 8 //3件物品,背包承重最大为8
1 6 10 //第一件物品, 重量为1,价值为6, 数目为10
2 10 5
2 20 2*/
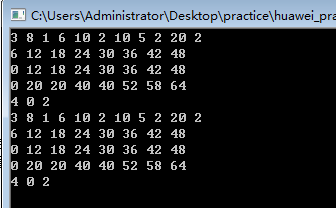
这是采用函数形式,注意定义函数调用矩阵时,用地址*。
四、
P04: 混合三种背包问题
问题
如果将P01、P02、P03混合起来。也就是说,有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)。应该怎么求解呢?
五、
P05: 二维费用的背包问题
问题
二维费用的背包问题是指:对于每件物品,具有两种不同的费用;选择这件物品必须同时付出这两种代价;对于每种代价都有一个可付出的最大值(背包容量)。问怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2,第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值(两种背包容量)分别为V和U。物品的价值为w[i]。
六、
P07: 有依赖的背包问题
简化的问题
这种背包问题的物品间存在某种“依赖”的关系。也就是说,i依赖于j,表示若选物品i,则必须选物品j。为了简化起见,我们先设没有某个物品既依赖于别的物品,又被别的物品所依赖;另外,没有某件物品同时依赖多件物品。
七、
P08: 泛化物品
定义
考虑这样一种物品,它并没有固定的费用和价值,而是它的价值随着你分配给它的费用而变化。这就是泛化物品的概念。
更严格的定义之。在背包容量为V的背包问题中,泛化物品是一个定义域为0..V中的整数的函数h,当分配给它的费用为v时,能得到的价值就是h(v)。
八、
P09: 背包问题问法的变化
以上涉及的各种背包问题都是要求在背包容量(费用)的限制下求可以取到的最大价值,但背包问题还有很多种灵活的问法,在这里值得提一下。但是我认为,只要深入理解了求背包问题最大价值的方法,即使问法变化了,也是不难想出算法的。
例如,求解最多可以放多少件物品或者最多可以装满多少背包的空间。这都可以根据具体问题利用前面的方程求出所有状态的值(f数组)之后得到。
还有,如果要求的是“总价值最小”“总件数最小”,只需简单的将上面的状态转移方程中的max改成min即可。
下面说一些变化更大的问法。