线性回归诊断--R
【转载时请注明来源】:http://www.cnblogs.com/runner-ljt/
Ljt 勿忘初心 无畏未来
作为一个初学者,水平有限,欢迎交流指正。
R--线性回归诊断(一) 主要介绍了线性回归诊断的主要内容和基本方法。
本文作为R中线性回归诊断的进一步延伸,将主要介绍用car包中的相关函数就行线性回归诊断。
>
> head(bank)
y x1 x2 x3 x4
1 1018.4 96259 2239.1 50760 1132.3
2 1258.9 97542 2619.4 39370 1146.4
3 1359.4 98705 2976.1 44530 1159.9
4 1545.6 100072 3309.1 39790 1175.8
5 1761.6 101654 3637.9 33130 1212.3
6 1960.8 103008 4020.5 34710 1367.0
> fline<-lm(y~x1+x2+x3+x4,data=bank)
>
正太性检验:
qqPlot
相较于 plot()函数,画更为精确的学生化残差图。
> qqPlot(fline)
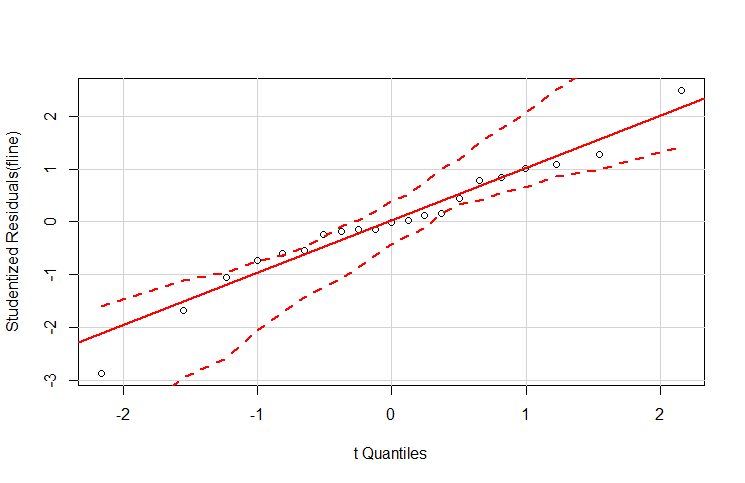
直线两侧的虚曲线代表置信区间,落在两曲线外的点可以认为是离群点。
线性检验:
crPlots
可通过成分残差图即偏残差图,判断因变量与自变量之间是否呈非线性关系,这种处理在检验线性关系的时候可以排除掉其他自变量的影响。
散点的 横轴为Xi ,纵轴为 Θi*Xi +ε
可以通过红线和绿线趋势是否一致来判断线性关系。(红线为 y=Θi*Xi ; 绿线为散点的趋势曲线)
> crPlots(fline)

异方差检验:
ncvTest
原假设:随机误差的方差不变 ------- P值>0.05 则接受原假设,即不存在明显的异方差现象。
> > ncvTest(fline) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 0.2017512 Df = 1 p = 0.653311 >
P值=0.653311>0.05 故不存在异方差情况。
spreadLevelPlot
创建标准化残差绝对值与拟合值的散点图。
若输出结果建议幂次变换(suggested power transformation)接近1,则异方差不明显,即不需要进行变换;
若幂次变换为0.5,则用根号y代替y;
若幂次变换为0,则用对数变换。
> > spreadLevelPlot(fline) Suggested power transformation: 0.5969254 >

自相关性检验:
在线性回归模型基本假设中有 cov(εi ,εj)=0 的假设,如果一个模型不满足该式则称随机误差项之间存在自相关现象。
注意:这里的自相关不是指两个或两个以上的变量之间的相关关系,而是指一个变量前后期数值之间的相关关系。
原假设:随机误差之间存在相关性。 -------P值>0.05 拒绝原假设,即不存在自相关现象。
> > durbinWatsonTest(fline) lag Autocorrelation D-W Statistic p-value 1 0.3578255 1.25138 0 Alternative hypothesis: rho != 0 >
从结果可以看出 P<0.05 接受原假设,存在严重自相关性。
共线性检验:
vif
VIF:variance inflation factor 方差扩大因子
一般情况下,VIFi>10 就表明存在多重共线性问题;而方程的多重共线性就是由VIF>10的这几个变量引起的。
>
> fline1<-lm(y~x1+x2+x4,data=bank)
> vif(fline1)
x1 x2 x4
4.830666 91.196064 88.411675
>
> cor(bank[,c(2,3,5)])
x1 x2 x4
x1 1.0000000 0.8904046 0.8867331
x2 0.8904046 1.0000000 0.9943239
x4 0.8867331 0.9943239 1.0000000
>
> fline2<-lm(y~x1+x4,data=bank)
> vif(fline2)
x1 x4
4.67936 4.67936
>
从回归方程 fline1的结果可以看出 X2与X4的VIF值明显的大于10,说明这两个变量之间存在着共线性;
同时,从简单相关系数矩阵也可以看出X2与X4之间的相关系数为0.9943239,表明两者之间高度相关。
可以通过删除VIF最大的变量来消除多从共线性,在删除X2后回归方程 fline2的结果就不存在明显的多重共线性现象。
异常值检验:
异常值点分为两种情况:(1)关于因变量y异常;(2)关于自变量x异常
(1)离群点 :预测效果不佳的点,具有加大残差。
outlierTest
根据最大的残差值的显著性来判断是否存在离群点。
若不显著 Bonferonni P>0.05 ,表明没有离群点;
若显著 Bonferonni P<0.05 ,表明该最大残差值点为离群点,需要删去,然后对删除该点后的拟合模型再次进行离群点的检验。
>
> outlierTest(fline)
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
16 -2.879438 0.011463 0.24071
>
(2)高杠杆点
距离样本总体较远的点,对回归参数影响加大。
杠杆值大于均值的2~3倍的样本点即可认为是高杠杆点。
>
> hatvalues(fline)
1 2 3 4 5 6 7
0.4453268 0.1937509 0.1943925 0.1376962 0.2137907 0.1647341 0.2542901
8 9 10 11 12 13 14
0.1114443 0.1203456 0.1075918 0.1372937 0.1113233 0.2690678 0.2546604
15 16 17 18 19 20 21
0.1712032 0.1200677 0.2205161 0.3279132 0.3918183 0.2912191 0.7615544
>
从各样本点的杠杆值可以看出 第21个样本点的杠杆值明显较大,为高杠杆点。
(3)强影响点
对模型的参数估计有较大的影响的点(综合考虑了残差和杠杆值),若将其删除则会导致模型发生本质的改变。
线性回归的杠杆值表示自变量的观测值与自变量平均值之间距离的远近;
较大的杠杆值的残差偏小,这是因为杠杆值大的观测点远离样本中心,能够把方程拉向自身,因而把杠杆值大的样本点称为强影响点;
强影响点对回归效果通常有较强的影响:
1.在实际问题中,因变量与自变量的线性关系只是在一定范围内成立,强影响点远离样本中心,因变量与自变量间可能不再是线性函
数关系,因而在选择回归函数形式时会侧重强影响点,
2.即使线性回归形式成立,但强影响点远离样本中心,能把回归方程拉向自身,使方程产生偏移
可以通过Cook距离来判断
> cooks.distance(fline)
1 2 3 4 5
1.146928e-01 8.816365e-06 1.721683e-03 1.180151e-02 5.950745e-02
6 7 8 9 10
1.188010e-02 1.049215e-03 1.595864e-02 5.529126e-03 7.215198e-04
11 12 13 14 15
1.040969e-05 5.131290e-04 3.465269e-01 1.077292e-01 1.045665e-01
16 17 18 19 20
1.554358e-01 1.388942e-03 1.154579e-01 1.330203e-01 5.371479e-03
21
3.517750e-01
>
第21个样本点的Cook值明显偏大,故具有较强的影响。
influence.measures
样本点有强影响则在右侧用 * 标记
>
> influence.measures(fline)
Influence measures of
lm(formula = y ~ x1 + x2 + x3 + x4, data = bank) :
dfb.1_ dfb.x1 dfb.x2 dfb.x3 dfb.x4 dffit cov.r cook.d hat inf
1 0.45826 -0.568459 0.055623 0.512937 0.009836 0.75016 1.981 1.15e-01 0.445 *
2 -0.00507 0.004561 -0.000964 0.000134 0.000275 -0.00643 1.713 8.82e-06 0.194
3 -0.06156 0.064613 -0.021146 -0.035703 0.013871 -0.08994 1.695 1.72e-03 0.194
4 -0.15306 0.124729 -0.077062 0.020415 0.062390 -0.23797 1.425 1.18e-02 0.138
5 -0.19112 0.045121 -0.136219 0.376396 0.126321 -0.54719 1.232 5.95e-02 0.214
6 -0.05657 -0.004141 -0.023041 0.165138 0.024055 -0.23824 1.503 1.19e-02 0.165
7 0.00462 0.013033 -0.013136 -0.058289 0.012084 0.07016 1.843 1.05e-03 0.254
8 -0.01447 -0.000661 -0.180381 0.032928 0.169471 0.27911 1.269 1.60e-02 0.111
9 -0.03729 0.017606 -0.096442 0.056441 0.084377 0.16202 1.473 5.53e-03 0.120
10 -0.02597 0.030394 -0.027975 -0.018465 0.020941 0.05821 1.533 7.22e-04 0.108
11 -0.00312 0.002135 -0.000075 0.004076 -0.000837 0.00699 1.600 1.04e-05 0.137
12 0.03346 -0.031808 0.013247 -0.004924 -0.005163 -0.04908 1.544 5.13e-04 0.111
13 -0.88710 1.114394 -0.618970 -0.968065 0.435245 1.51702 0.331 3.47e-01 0.269 *
14 -0.46471 0.322235 -0.157021 0.463529 0.054450 0.74845 1.103 1.08e-01 0.255
15 0.54324 -0.482824 -0.052544 -0.244757 0.172698 -0.76306 0.704 1.05e-01 0.171
16 0.76658 -0.744780 0.123881 -0.025557 0.011793 -1.06364 0.174 1.55e-01 0.120
17 0.01766 -0.010056 -0.043461 -0.040832 0.045946 -0.08075 1.758 1.39e-03 0.221
18 0.05049 0.055714 0.583416 -0.186662 -0.554400 0.76448 1.399 1.15e-01 0.328
19 0.20494 -0.110758 0.593949 -0.153020 -0.518155 0.81642 1.627 1.33e-01 0.392
20 -0.04819 0.059309 -0.002337 -0.027989 -0.022679 -0.15900 1.909 5.37e-03 0.291
21 -0.20629 0.281238 0.822119 0.113466 -0.986662 -1.30680 4.861 3.52e-01 0.762 *
>
>
从结果来看 第1,13,21 个样本点的影响较大。
influencePlot
将离群点、高杠杆点、强影响点整合到一个图中。
纵坐标在 -2~2之外的可以认为是离群点;
横坐标为杠杆值;
圆圈大小代表影响值大小。
