1、二叉搜索树:去一个陌生的城市问路到目的地;
for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>).
给予一个已经排序好的整数数组, 生成一个相对合理的二叉搜索树。(?相对合理的?)
给予一个二叉树的根节点,验证该树是否是二叉树搜索树,(在O(n)时间内), 请用你熟悉的语言写出算法。
<60 bad
<70 pass
<80 general
<90 good
excellent
最优二叉树
霍夫曼树
树的带权路径长度为为树中所有叶子节点的带权路径长度之和
带权路径长度最小的二叉树
https://zh.wikipedia.org/wiki/B树
B树,概括来说是一个一般化的二元搜尋樹(binary search tree),可以拥有多于2个子节点
https://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html
Binary Trees
Introduction
| We extend the concept of linked data structures to structure containing nodes with more than one self-referenced field. A binary tree is made of nodes, where each node contains a "left" reference, a "right" reference, and a data element. The topmost node in the tree is called the root.
Every node (excluding a root) in a tree is connected by a directed edge from exactly one other node. This node is called a parent. On the other hand, each node can be connected to arbitrary number of nodes, called children. Nodes with no children are called leaves, or external nodes. Nodes which are not leaves are called internal nodes. Nodes with the same parent are called siblings. |
 |
More tree terminology:
- The depth of a node is the number of edges from the root to the node.
- The height of a node is the number of edges from the node to the deepest leaf.
- The height of a tree is a height of the root.
- A full binary tree.is a binary tree in which each node has exactly zero or two children.
- A complete binary tree is a binary tree, which is completely filled, with the possible exception of the bottom level, which is filled from left to right.

A complete binary tree is very special tree, it provides the best possible ratio between the number of nodes and the height. The height h of a complete binary tree with N nodes is at most O(log N). We can easily prove this by counting nodes on each level, starting with the root, assuming that each level has the maximum number of nodes:
n = 1 + 2 + 4 + ... + 2^(h-1)+2^h
=2^(h+1)-1
Solving this with respect to h, we obtain
h = O(log n)
where the big-O notation hides some superfluous details.
满二叉树:深度为k且有2^k-1个节点的二叉树
Advantages of trees
Trees are so useful and frequently used, because they have some very serious advantages:
- Trees reflect structural relationships in the data
- Trees are used to represent hierarchies
- Trees provide an efficient insertion and searching
- Trees are very flexible data, allowing to move subtrees around with minumum effort
Traversals
A traversal is a process that visits all the nodes in the tree. Since a tree is a nonlinear data structure, there is no unique traversal. We will consider several traversal algorithms with we group in the following two kinds
- depth-first traversal
- breadth-first traversal
There are three different types of depth-first traversals, :
- PreOrder traversal - visit the parent first and then left and right children;
- InOrder traversal - visit the left child, then the parent and the right child;
- PostOrder traversal - visit left child, then the right child and then the parent;
There is only one kind of breadth-first traversal--the level order traversal. This traversal visits nodes by levels from top to bottom and from left to right.
深度优先3种
前序遍历 按序遍历 后序遍历
广度优先1种
按层遍历
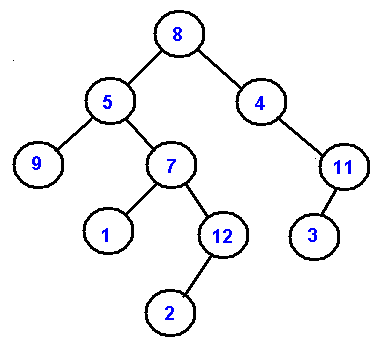
PreOrder - 8, 5, 9, 7, 1, 12, 2, 4, 11, 3
InOrder - 9, 5, 1, 7, 2, 12, 8, 4, 3, 11
PostOrder - 9, 1, 2, 12, 7, 5, 3, 11, 4, 8
LevelOrder - 8, 5, 4, 9, 7, 11, 1, 12, 3, 2
http://cslibrary.stanford.edu/110/BinaryTrees.html
Binary Trees
This article introduces the basic concepts of binary trees, and then works through a series of practice problems with solution code in C/C++ and Java. Binary trees have an elegant recursive pointer structure, so they are a good way to learn recursive pointer algorithms.
Contents
Section 1. Binary Tree Structure -- a quick introduction to binary trees and the code that operates on them
Section 2. Binary Tree Problems -- practice problems in increasing order of difficulty
Section 3. C Solutions -- solution code to the problems for C and C++ programmers
Section 4. Java versions -- how binary trees work in Java, with solution code
Stanford CS Education Library -- #110
This is article #110 in the Stanford CS Education Library. This and other free CS materials are available at the library (http://cslibrary.stanford.edu/). That people seeking education should have the opportunity to find it. This article may be used, reproduced, excerpted, or sold so long as this paragraph is clearly reproduced. Copyright 2000-2001, Nick Parlante, nick.parlante@cs.stanford.edu.
Related CSLibrary Articles
- Linked List Problems (http://cslibrary.stanford.edu/105/) -- a large collection of linked list problems using various pointer techniques (while this binary tree article concentrates on recursion)
- Pointer and Memory (http://cslibrary.stanford.edu/102/) -- basic concepts of pointers and memory
- The Great Tree-List Problem (http://cslibrary.stanford.edu/109/) -- a great pointer recursion problem that uses both trees and lists
Section 1 -- Introduction To Binary Trees
A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree. The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree.
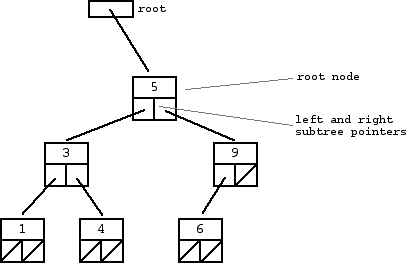
A "binary search tree" (BST) or "ordered binary tree" is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>). The tree shown above is a binary search tree -- the "root" node is a 5, and its left subtree nodes (1, 3, 4) are <= 5, and its right subtree nodes (6, 9) are > 5. Recursively, each of the subtrees must also obey the binary search tree constraint: in the (1, 3, 4) subtree, the 3 is the root, the 1 <= 3 and 4 > 3. Watch out for the exact wording in the problems -- a "binary search tree" is different from a "binary tree".
二叉搜索树,为什么叫“有序二叉树”?对于任一个节点,左子树的元素都不比该节点大,右...大。注意这个限制条件。
The nodes at the bottom edge of the tree have empty subtrees and are called "leaf" nodes (1, 4, 6) while the others are "internal" nodes (3, 5, 9).
Binary Search Tree Niche
Basically, binary search trees are fast at insert and lookup. The next section presents the code for these two algorithms. On average, a binary search tree algorithm can locate a node in an N node tree in order lg(N) time (log base 2). Therefore, binary search trees are good for "dictionary" problems where the code inserts and looks up information indexed by some key. The lg(N) behavior is the average case -- it's possible for a particular tree to be much slower depending on its shape.
Strategy
Some of the problems in this article use plain binary trees, and some use binary search trees. In any case, the problems concentrate on the combination of pointers and recursion. (See the articles linked above for pointer articles that do not emphasize recursion.)
For each problem, there are two things to understand...
- The node/pointer structure that makes up the tree and the code that manipulates it
- The algorithm, typically recursive, that iterates over the tree
When thinking about a binary tree problem, it's often a good idea to draw a few little trees to think about the various cases.
Typical Binary Tree Code in C/C++
As an introduction, we'll look at the code for the two most basic binary search tree operations -- lookup() and insert(). The code here works for C or C++. Java programers can read the discussion here, and then look at the Java versions in Section 4.
In C or C++, the binary tree is built with a node type like this...
struct node {
int data;
struct node* left;
struct node* right;
}
Lookup()
Given a binary search tree and a "target" value, search the tree to see if it contains the target. The basic pattern of the lookup() code occurs in many recursive tree algorithms: deal with the base case where the tree is empty, deal with the current node, and then use recursion to deal with the subtrees. If the tree is a binary search tree, there is often some sort of less-than test on the node to decide if the recursion should go left or right.
/*
Given a binary tree, return true if a node
with the target data is found in the tree. Recurs
down the tree, chooses the left or right
branch by comparing the target to each node.
*/
static int lookup(struct node* node, int target) {
// 1. Base case == empty tree
// in that case, the target is not found so return false
if (node == NULL) {
return(false);
}
else {
// 2. see if found here
if (target == node->data) return(true);
else {
// 3. otherwise recur down the correct subtree
if (target < node->data) return(lookup(node->left, target));
else return(lookup(node->right, target));
}
}
}
The lookup() algorithm could be written as a while-loop that iterates down the tree. Our version uses recursion to help prepare you for the problems below that require recursion.
Pointer Changing Code
There is a common problem with pointer intensive code: what if a function needs to change one of the pointer parameters passed to it? For example, the insert() function below may want to change the root pointer. In C and C++, one solution uses pointers-to-pointers (aka "reference parameters"). That's a fine technique, but here we will use the simpler technique that a function that wishes to change a pointer passed to it will return the new value of the pointer to the caller. The caller is responsible for using the new value. Suppose we have a change() function that may change the the root, then a call to change() will look like this...
// suppose the variable "root" points to the tree
root = change(root);
We take the value returned by change(), and use it as the new value for root. This construct is a little awkward, but it avoids using reference parameters which confuse some C and C++ programmers, and Java does not have reference parameters at all. This allows us to focus on the recursion instead of the pointer mechanics. (For lots of problems that use reference parameters, see CSLibrary #105, Linked List Problems, http://cslibrary.stanford.edu/105/).
Insert()
Insert() -- given a binary search tree and a number, insert a new node with the given number into the tree in the correct place. The insert() code is similar to lookup(), but with the complication that it modifies the tree structure. As described above, insert() returns the new tree pointer to use to its caller. Calling insert() with the number 5 on this tree...
2
/
1 10
returns the tree...
2
/
1 10
/
5
The solution shown here introduces a newNode() helper function that builds a single node. The base-case/recursion structure is similar to the structure in lookup() -- each call checks for the NULL case, looks at the node at hand, and then recurs down the left or right subtree if needed.
/*
Helper function that allocates a new node
with the given data and NULL left and right
pointers.
*/
struct node* NewNode(int data) {
struct node* node = new(struct node); // "new" is like "malloc"
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/*
Give a binary search tree and a number, inserts a new node
with the given number in the correct place in the tree.
Returns the new root pointer which the caller should
then use (the standard trick to avoid using reference
parameters).
*/
struct node* insert(struct node* node, int data) {
// 1. If the tree is empty, return a new, single node
if (node == NULL) {
return(newNode(data));
}
else {
// 2. Otherwise, recur down the tree
if (data <= node->data) node->left = insert(node->left, data);
else node->right = insert(node->right, data);
return(node); // return the (unchanged) node pointer
}
}
The shape of a binary tree depends very much on the order that the nodes are inserted. In particular, if the nodes are inserted in increasing order (1, 2, 3, 4), the tree nodes just grow to the right leading to a linked list shape where all the left pointers are NULL. A similar thing happens if the nodes are inserted in decreasing order (4, 3, 2, 1). The linked list shape defeats the lg(N) performance. We will not address that issue here, instead focusing on pointers and recursion.
Binary search tree - Wikipedia https://en.wikipedia.org/wiki/Binary_search_tree
SortedSequences.pdf http://people.mpi-inf.mpg.de/~mehlhorn/ftp/Toolbox/SortedSequences.pdf
7.1 Binary Search Trees
Navigating a search tree is a bit like asking your way around in a foreign city. You
ask a question, follow the advice given, ask again, follow the advice again, . . . , until
you reach your destination. A binary search tree is a tree whose leaves store the elements of a sorted sequence
in sorted order from left to right. In order to locate a key
k, we start at the root of the tree and follow the unique path to the appropriate leaf. How do we identify the
correct path? To this end, the interior nodes of a search tree store keys that guide the
search; we call these keys splitter keys. Every nonleaf node in a binary search tree
with n≥2 leaves has exactly two children, a left child and a right child. The splitter
key s associated with a node has the property that all keys
k stored in the left subtree
satisfy k≤s and all keys k stored in the right subtree satisfy k>s.
With these definitions in place, it is clear how to identify the correct path when
locating k. Let s be the splitter key of the current node. If k≤s, go left. Otherwise,
go right. Figure 7.2 gives an example. Recall that the height of a tree is the length
of its longest root–leaf path. The height therefore tells us the maximum number of
search steps needed to locate a leaf.
每个节点左子树的键key不比该节点处的key大,右子树的key比该节点处的key大。