leetcode50之爬楼梯

题目描述：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶
来源：https://leetcode-cn.com/problems/climbing-stairs/

代码实现：

def climbStairs(n):
    '''
    动态规划求解
    :return:
    '''
    dp = [0] * (n + 1)
    dp[0] = 1
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]

    return dp[n]


print('------测试climbStairs()--------')
print(climbStairs(5))


def climbStairs1(n):
    '''
    斐波那契额数列求解
    :return:
    '''
    a = pow(0.5 * (1 + 5 ** 0.5), n + 1) - pow(0.5 * (1 - 5 ** 0.5), n + 1)
    res = 1 / (5 ** 0.5) * a

    return int(res)


print('------测试climbStairs()--------')
print(climbStairs1(5))

总结：动态规划：在整个爬楼梯过程中，每次既可以迈1步，也可以迈两步。假设要爬阶数为n的楼梯，用dp[n]表示爬n阶楼梯所有爬法，当第一步为1时，剩下楼梯爬法为dp[n-1];当第一步为2时，剩下楼梯爬法为dp[n-2]。因此可得出动态规划方程为dp[n]=dp[n-1]+dp[n-2]。求取边界条件dp[1]=1(台阶数为1 时，只有一种爬法)，dp[0]=1(假设条件）根据上述动态方程可编码如方法1所示

斐波那契数列求解：从动态规划转移方程可以看出，存在递推公式dp[n]=dp[n-1]+dp[n-2],dp[0]=1,dp[1]=1(n>=2),此递推公式正好是斐波那契递推公式（从1开始，题目从0开始）

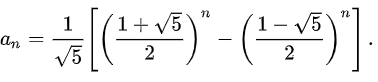编码如方法2