LCA-求树上两点最近公共祖先问题
lrj的紫书上提供了一种将LCA问题转化为RMQ问题的方法,即dfs一次处理出一个序列,first(u)代表u第一次出现的下标,则对于u,v的最近公共祖先的下标即为RMQ(first(u), first(v))。
LCA->RMQ(在线处理):
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N = 40010, M = 25; 4 int ver[2*N], R[2*N], first[N], dir[N], dp[2*N][M], tot; 5 /*ver[i]保存下标为i的结点编号,R[i]为下标为i的结点深度,first[i]为编号为i的结点第一次出现的下标, 6 dp[i][j]为起始下标为i,长度为1<<j的区间的最小深度的结点的下标*/ 7 bool vis[N]; 8 struct Node { 9 int to, w; 10 }; 11 vector<Node> G[N]; 12 13 void dfs(int u, int dep) { 14 vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep; 15 for (int i = 0; i < G[u].size(); ++i) { 16 int v = G[u][i].to, w = G[u][i].w; 17 dir[v] = dir[u] + w; 18 if (vis[v]) continue; 19 dfs(v, dep+1); 20 ver[++tot] = u; R[tot] = dep; 21 } 22 } 23 24 void RMQ_init(int l, int r) { 25 for (int i = l; i <= r; ++i) dp[i][0] = ver[i]; 26 for (int k = 1; (1<<k) <= r-l+1; ++k) 27 for (int i = l; i + (1<<k) <= r; ++i) { 28 int a = dp[i][k-1], b = dp[i+(1<<(k-1))][k-1]; 29 if (R[a] > R[b]) dp[i][k] = b; 30 else dp[i][k] = a; 31 } 32 } 33 34 int RMQ(int l, int r) { 35 int k = 0; 36 while ((1<<(k+1)) <= r-l+1) ++k; 37 int a = dp[l][k], b = dp[r-(1<<k)][k]; 38 if (R[a] > R[b]) return b; 39 else return a; 40 } 41 42 int LCA(int u, int v) { 43 int x = first[u], y = first[v]; 44 if (x > y) swap(x, y); 45 int res = RMQ(x, y); 46 return ver[res]; 47 } 48 49 int main() { 50 int n; 51 while (cin >> n) { 52 memset(dir, 0, sizeof(dir)); 53 memset(vis, 0, sizeof(vis)); 54 for (int i = 1; i <= n; ++i) G[i].clear(); 55 tot = 0; 56 int a, b, c; 57 for (int i = 1; i < n; ++i) { 58 cin >> a >> b >> c; 59 G[a].push_back(Node{b, c}); 60 } 61 dfs(1, 1); 62 RMQ_init(1, 2*n-1); 63 int q, u, v; 64 cin >> q; 65 while (q--) { 66 cin >> u >> v; 67 cout << LCA(u, v) << endl; 68 } 69 } 70 71 return 0; 72 }
Tarjan算法(离线处理):
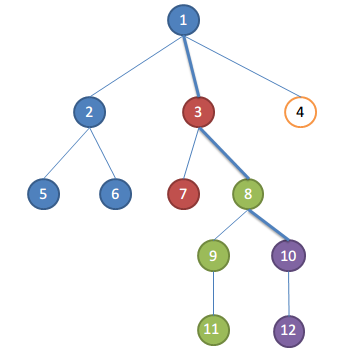
具体思想不再阐述,下图代表处理编号10的结点的询问时的状态(同色代表处于同一个集合);
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 10005; 4 int p[maxn], anc[maxn]; 5 bool vis[maxn]; 6 vector<int> G[maxn]; 7 vector<int> q[maxn]; 8 9 int find(int x) {return x == p[x] ? x : p[x] = find(p[x]);} 10 11 void Union(int x, int y) { 12 x = find(x); y = find(y); 13 if (x == y) return; 14 p[y] = x; 15 } 16 17 void LCA(int u) { 18 anc[u] = u; 19 for (int i = 0; i < G[u].size(); ++i) { 20 int v = G[u][i]; 21 LCA(v); 22 Union(u, v); 23 anc[find(u)] = u; 24 } 25 vis[u] = true; 26 for (int i = 0; i < q[u].size(); ++i) { 27 int v = q[u][i]; 28 if (!vis[v]) continue; 29 printf("LCA(%d, %d): %d ", u, v, anc[find(v)]); 30 } 31 } 32 33 int main() { 34 int n; 35 while (~scanf("%d", &n)) { 36 int a, b, k; 37 memset(vis, 0, sizeof(vis)); 38 for (int i = 1; i <= n; ++i) G[i].clear(), p[i] = i; 39 for (int i = 1; i < n; ++i) { 40 scanf("%d%d", &a, &b); 41 G[a].push_back(b); 42 } 43 scanf("%d", &k); 44 for (int i = 0; i < k; ++i) q[i].clear(); 45 while (k--) { 46 scanf("%d%d", &a, &b); 47 q[a].push_back(b); 48 q[b].push_back(a); 49 } 50 LCA(1); 51 } 52 53 return 0; 54 }