2015 提高组 信息传递--tarjan找最小环

P2661 信息传递 

题目描述

有 n 个同学（编号为 1 到 n ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 i 的同学的信息传递对象是编号为 Ti​ 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

共 2 行。

第 1 行包含1个正整数 n ，表示 n 个人。

第 2 行包含 n 个用空格隔开的正整数 T1​,T2​,⋯⋯,Tn​ ，其中第 i个整数 Ti​ 表示编号为 i 的同学的信息传递对象是编号为 Ti​ 的同学， Ti​≤n 且Ti​≠i 。

输出格式：

1 个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1： 

5
2 4 2 3 1

输出样例#1： 

3

说明

样例1解释

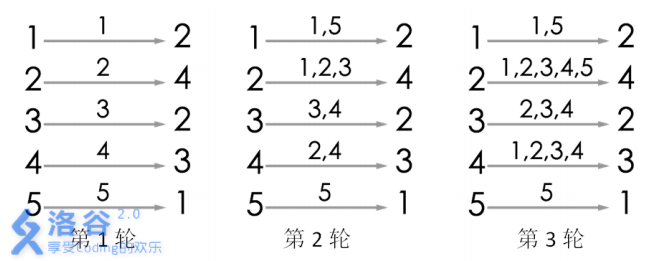
游戏的流程如图所示。当进行完第 3 轮游戏后， 4 号玩家会听到 2 号玩家告诉他自己的生日，所以答案为 3 。当然，第 3 轮游戏后， 2 号玩家、 3 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 30% 的数据， n≤200 ；

对于 60% 的数据， n≤2500 ；

对于 100% 的数据， n≤200000 。

这题暴力的话好像是真的难写。

信息传递，在两个可以相互传递的人之间连边(单向)，表示信息的传递，然后这个题不就变成了，求从图中某一个点的出发绕回自己的最短路径了吗，显然这不就是利用tarjan求最小环么？

所以这题不就解决了嘛。

#include <iostream>
#include <cstdio>
#define N int(2e5+2)
using namespace std;
struct ahah{
    int nxt,to;
}edge[N];
int n,x,ans,vis[N];
int head[N],tot;
void add(int x,int y)
{
    edge[++tot].nxt=head[x],edge[tot].to=y,head[x]=tot;
} 
int dfn[N],low[N],index;
int stack[N],top;
bool in[N];
int belong[N],cnt;
void tarjan(int s)
{
    dfn[s]=low[s]=++index;
    in[s]=1;stack[++top]=s;
    for(int i=head[s];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            if(low[v]<low[s])low[s]=low[v];
        }
        else if(in[v]&&low[s]>dfn[v])low[s]=dfn[v];
    }
    if(dfn[s]==low[s])
    {
        int p;
        cnt++;
        do
        {
            p=stack[top--];
            in[p]=0;
            belong[p]=cnt;
        }while(p!=s);
    }
}
int main()
{
     ans=99999999;
     scanf("%d",&n);
     for(int i=1;i<=n;i++)scanf("%d",&x),add(i,x);
     for(int i=1;i<=n;i++)
         if(!dfn[i])tarjan(i);
    for(int i=1;i<=n;i++)vis[belong[i]]++;
    for(int i=1;i<=n;i++)
    {
        if(vis[i]>1)ans=min(ans,vis[i]);
    }
    printf("%d",ans);
}